Scientific Python
Python dispose d’un environnement scientifique très puissant reférencé sous le nom de SciPy (Scientific Python) stack avec trois modules principaux:
NumPy : package apportant une structure de données de plus grande efficacité algorithmique que les listes (Numpy array) et les opérations permettant de manipuler très efficacement cette structure de données (indexing, sorting, reshaping, vectorisation, etc…)
SciPy : package contenant un grand nombre d’algorithmes scientifiques utilisant les structures de données de NumPy.
Matplotlib : package contenant des fonctions de tracé de figures scientifiques.
Ce chapitre présente le strict minimum des packages NumPy et Matplotlib.
Numpy
Les listes de Python sont des containers hétérogènes très efficaces pour les opérations courantes. Leur universalité est cependant incompatible avec une grande efficacité algorithmique. Numpy introduit la notion de tableau multi dimensionnel homogène, en ce sens qu’il ne peut contenir que des données numériques de même nature. Ces données sont indexées par un tuple d’entiers positifs. Il y a autant d’entiers que de dimensions dans le tableau. Dans la terminologie Numpy, les dimensions s’appellent des axes. Le nombre d’axes définit le rang du tableau.
Le tableau
Le tableau Numpy est un ndarray. Un exemple simple d’utilisation:
>>> import numpy as np
>>> a = np.arange(12)
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>> type(a)
<class 'numpy.ndarray'>
La fonction arange() fonctionne de la même façon que la fonction range() de Python mais retourne un ndarray plutôt qu’une liste. L’objet ndarray possède un certain nombre d’attributs contenant ses caractéristiques:
>>> a.shape
(12,)
>>> a.ndim
1
>>> a.dtype
dtype('int32')
>>> a.size
12
La méthode reshape() est utilisée pour organiser les données sur plusieurs dimensions:
>>> a.reshape(3,4)
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>> a.reshape(4,3)
array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
Si les paramètres de reshape() ne sont pas compatibles avec les données une exception ValueError est levée:
>>> a.reshape(4,4)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: total size of new array must be unchanged
Création d’un tableau
Le constructeur de la classe ndarray accepte une séquence Python comme argument:
>>> l = [ i**2 for i in range(5) ]
>>> l
[0, 1, 4, 9, 16]
>>> a = np.array(l) # l'argument est une liste
>>> a
array([ 0, 1, 4, 9, 16])
>>> a = np.array((1, 2, 3)) # l'argument est un tuple
>>> a
array([1, 2, 3])
Les méthodes de tableau
Le tableau ndarray dispose d’un grand nombre de méthodes permettant de réaliser des opérations sur les tableaux avec une grande efficacité algorithmique. Quelques unes en action:
>>> a = np.array((6, 2, 1, 4, 5, 3))
>>> a.sum()
21
>>> a.cumprod()
array([ 6, 12, 12, 48, 240, 720], dtype=int32)
>>> a.cumsum()
array([ 6, 8, 9, 13, 18, 21], dtype=int32)
>>> a.max()
6
>>> a.min()
1
L’opération de tri sort() est conduite « sur place »:
>>> a.sort()
>>> a
array([1, 2, 3, 4, 5, 6])
On dispose également de méthodes statistiques:
>>> a.mean()
3.5
>>> a.std()
1.707825127659933
>>> a.var()
2.9166666666666665
Mais d’autres opérations statistiques sont possibles par l’intermédiaire de fonctions. Un exemple de l’utilisation de median():
>>> np.median(a)
3.5
Opérations sur les tableaux
Les opérations numériques sur les tableaux sont vectorisées. Inutile de parcourir les éléments du tableau avec une boucle. La syntaxe est concise, élégante et très efficace d’un point de vue algorithmique:
>>> a
array([1, 2, 3, 4, 5, 6])
>>> a*2
array([ 2, 4, 6, 8, 10, 12])
>>> b = a*2
>>> b
array([ 2, 4, 6, 8, 10, 12])
>>> c = b-1
>>> c
array([ 1, 3, 5, 7, 9, 11])
>>> d = a/c
>>> d
array([ 1., 0.66666667, 0.6, 0.57142857, 0.55555556, 0.54545455])
Slicing
L’accès à des éléments ou des portions d’un tableau ndarray utilise la même syntaxe que celle des séquences Python:
>>> a
array([1, 2, 3, 4, 5, 6])
>>> a[1:]
array([2, 3, 4, 5, 6])
>>> a[::2]
array([1, 3, 5])
>>> a[::-1]
array([6, 5, 4, 3, 2, 1])
Filtrage
On peut utiliser la vectorisation pour créer aisément un masque de filtrage:
>>> a > 3
array([False, False, False, True, True, True], dtype=bool)
Ce masque permet de mettre en oeuvre une fonctionnalité puissante de filtrage des éléments d’un tableau en étendant le concept de slicing. On peut en effet utiliser ce masque pour sélectionner ou non certains éléments du tableau. Sans surprise les éléments correspondant à True sont conservés, ceux correspondant à False sont écartés:
>>> a[a>3]
array([4, 5, 6])
Itérer sur un tableau
La vectorisation introduite par Numpy est une opération puissante qu’il faut privilégier. La très grande majorité des opérations sur les tableaux peut être traitée de cette façon. C’est une syntaxe concise, élégante, lisible (donc maintenable) et très efficace algorithmiquement. Dans le cas très particulier où la vectorisation ne conviendrait pas, on itère sur des tableaux, de la même manière que sur des séquences Python:
>>> for i in a:
... print(i)
...
1
2
3
4
5
6
Matplotlib
NumPy fournit une structure de donnée efficace (ndarray) ainsi que les méthodes/fonctions permettant de la manipuler. Un environnement de calcul scientifique doit également fournir les outils nécessaires pour tracer courbes et graphiques. Matplotlib est le framework graphique historique. Mais il souffre de plusieurs limitations et est maintenant remplacé par des solutions plus performantes, dont les deux principales sont Bokeh et Plotly.
Tracer une courbe
La fonction plot() permet de tracer une courbe 2D.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> x = np.linspace(0, np.pi*2)
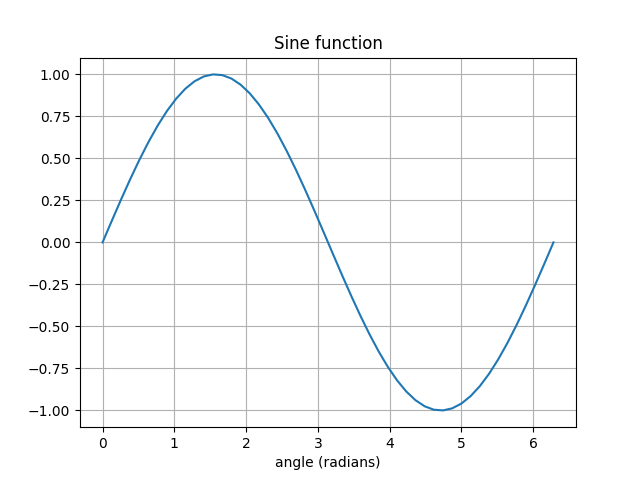
>>> plt.plot(x, np.sin(x))
[<matplotlib.lines.Line2D object at 0x7ffab289d1d0>]
>>> plt.title('Sine function')
Text(0.5, 1.0, 'Sine function')
>>> plt.xlabel('angle (radians)')
Text(0.5, 0, 'angle (radians)')
>>> plt.grid()
>>> plt.show()
linspace() génère un tableau de nombres réels compris entre 0 et 2 \(\pi\). La fonction sin() est vectorisée et génère un tableau de valeurs nécessaire pour l’affichage.
Tracer un histogramme
La fonction hist() permet de tracer l’histogramme d’un ensemble de données.
>>> x = np.random.randn(10000)
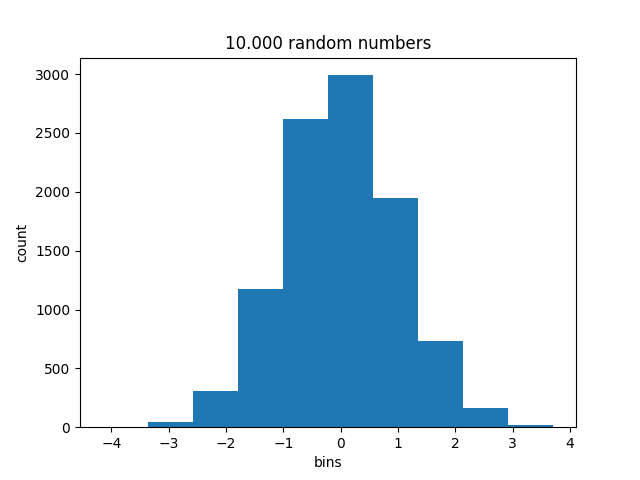
>>> n, bins, patches = plt.hist(x)
>>> n
array([ 3., 41., 307., 1177., 2620., 2991., 1951., 733., 161.,
16.])
>>> bins
array([-4.15566633, -3.36897652, -2.58228671, -1.7955969 , -1.00890709,
-0.22221727, 0.56447254, 1.35116235, 2.13785216, 2.92454197,
3.71123178])
>>> plt.title('10.000 random numbers')
Text(0.5, 1.0, '10.000 random numbers')
>>> plt.xlabel('bins')
Text(0.5, 0, 'bins')
>>> plt.ylabel('count')
Text(0, 0.5, 'count')
>>> plt.show()
n est un ndarray contenant le nombre d’échantillons dans chacune des classes dont les limites sont définie par le tableau bins comme le montre la figure produite.
La fonction hist() accepte d’autres arguments que les données à traiter. En particulier, le paramètre bins permet de définir les classes. Si c’est un entier bins représente le nombre de classes. Si c’est une séquence, les valeurs du tableau bins délimitent les classes. Cette délimitation peut être inhomogène.
>>> b = list(range(-4,5,1))
>>> b
[-4, -3, -2, -1, 0, 1, 2, 3, 4]
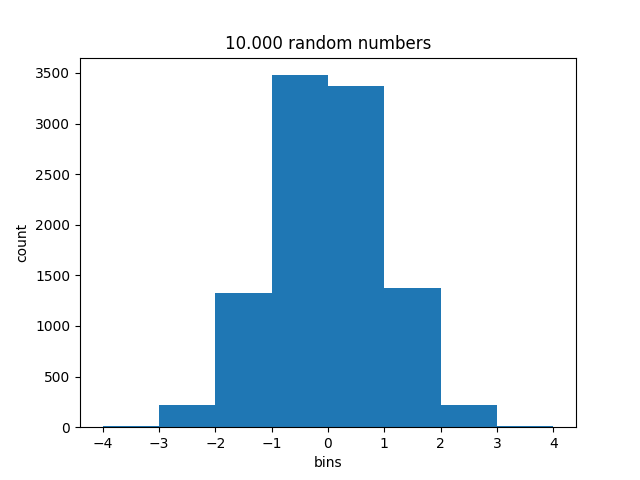
>>> n, bins, patches = plt.hist(x, bins=b)
>>> n
array([ 7., 219., 1324., 3478., 3373., 1371., 215., 12.])
>>> plt.title('10.000 random numbers')
Text(0.5, 1.0, '10.000 random numbers')
>>> plt.xlabel('bins')
Text(0.5, 0, 'bins')
>>> plt.ylabel('count')
Text(0, 0.5, 'count')
>>> plt.show()
La figure produite est différente:
Note
Les résultats obtenus peuvent être sensiblement différents d’une simulation à une autre, car les données générées sont pseudo aléatoires.
Ce qu’il faut retenir
Les graphiques Matplotlib ne peuvent pas être personnalisés avec des titres et des étiquettes
Les tableaux NumPy sont toujours plus lents que les listes Python
Les fonctions statistiques ne fonctionnent qu’avec des tableaux 1D
Les tableaux NumPy supportent le slicing avec la même syntaxe que les séquences Python
Il est impossible d’utiliser des boucles for avec les tableaux NumPy
Les opérations de filtrage sont plus lentes que les boucles Python
NumPy fournit une structure de données tableau multidimensionnel homogène plus efficace que les listes Python
La taille totale du tableau peut être modifiée avec
reshapeNumPy inclut des fonctions statistiques comme
mean,median,stdetvarLa vectorisation rend le code plus difficile à lire et à maintenir
Matplotlib ne peut créer que des graphiques en 2D
Les indices négatifs ne sont pas supportés dans le slicing NumPy
Les tableaux NumPy peuvent contenir des données de types différents dans la même structure
Le filtrage des tableaux NumPy peut être réalisé avec des masques booléens
reshapene fonctionne qu’avec des tableaux 2DIl est impossible de calculer plusieurs statistiques sur le même tableau
Les opérations sur les tableaux NumPy sont vectorisées, évitant l’utilisation de boucles explicites
Le pas (step) ne peut pas être négatif dans le slicing NumPy
Le filtrage crée toujours une copie complète du tableau
Matplotlib permet de créer des visualisations graphiques comme des courbes et des histogrammes
La méthode
reshapepermet de réorganiser un tableau NumPy en modifiant ses dimensionsLes calculs statistiques sont moins précis qu’avec les listes Python
NumPy ne peut gérer que des tableaux à une dimension
Le slicing en NumPy crée toujours une copie du tableau
Matplotlib nécessite toujours des données NumPy
La vectorisation ne fonctionne qu’avec les opérations mathématiques simples
Les masques de filtrage ne fonctionnent qu’avec des comparaisons d’égalité
reshape modifie toujours le tableau original