Suites de Syracuse

Contexte

On appelle suite de Syracuse une suite d’entiers naturels définie de la manière suivante :

• on part d’un nombre entier strictement positif ;
• s’il est pair, on le divise par 2 ;
• s’il est impair, on le multiplie par 3 et on ajoute 1.

En répétant l’opération, on obtient une suite d’entiers strictement positifs dont chacun ne dépend que de son prédécesseur.

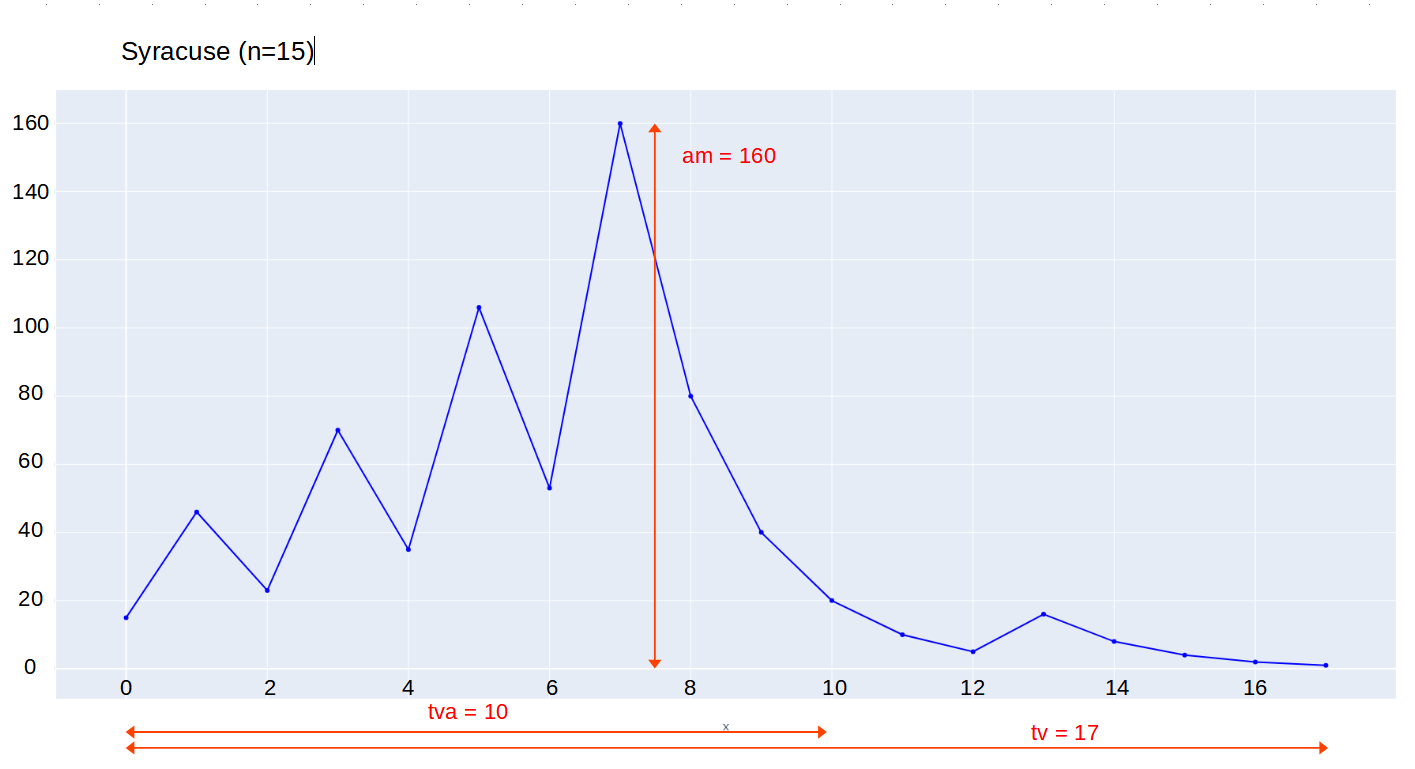
Pour une suite de Syracuse, le premier élément est noté \(u_{0}\). On définit trois métriques :

• le temps de vol : tv : c’est le plus petit indice \(k\) tel que \(u_{k}=1\).
  • \(tv = 17\) pour la suite de Syracuse de source \(n = 15\) ;
  • \(tv = 46\) pour la suite de Syracuse de source \(n = 127\).
• l’altitude maximale : am : c’est la valeur maximale de la suite. Elle est de
  • \(am = 160\) pour la suite de Syracuse de source \(n = 15\) ;
  • \(am = 4372\) pour la suite de Syracuse de source \(n = 127\).
• le temps de vol en altitude : tva : c’est le plus petit indice \(k\) tel que \(u_{k+1} < u_{0}\).
  • \(tva = 10\) pour la suite de Syracuse de source \(n = 15\) ;
  • \(tva = 23\) pour la suite de Syracuse de source \(n = 127\) ;

Ces métriques sont illustrées par la figure ci dessous.

Environnement de travail

Créer un fichier python-04-fonctions-suites-syracuse.py.

Selon la convention de structuration des modules, ce fichier sera structuré en quatre parties :

1. Imports et définition des variables globales est vide car on ne fait pas appel à des packages externes, ni à des variables globales ;
2. Définition des fonctions secondaires ;
3. Définition de la fonction principale contient l’appel aux fonctions secondaires ;
4. Appel protégé de la fonction principale.

Objectifs

L’objectif est d’écrire une fonction syracuse() :

• qui prend en paramètre un entier \(n\) ;
• et retourne les 3 métriques précédentes.

La structure est la suivante

def syracuse(n):

    pass

    # initialisation des variables

    # tant que la suite n'est pas terminée :
    #   - calcul du n suivant
    #   - mise à jour du temps de vol (tv)
    #   - mise à jour du temps de vol en altitude (tva) si nécessaire
    #   - mise à jour de l'altitude maximale (am)

    # retour de tv, tva, am


def main():
    # exemple d'exécution
    n = 15
    tv, tva, am = syracuse(n)
    print(n, tv, tva, am)

if __name__ == "__main__":
    main()

Utilisez la fonction syracuse() pour calculer les suites pour \(n = 15\) et \(n = 127\). Vérifier que les métriques obtenues sont conformes aux valeurs ci dessus.

Utilisez ensuite la fonction syracuse() pour calculer :

• la valeur maximum de l’altitude maximale des suites de Syracuse pour \(n = 1\) jusqu’à \(n = 9999\) ;
• la valeur maximum du temps de vol des suites de Syracuse pour \(n = 1\) jusqu’à \(n = 9999\) ;
• la valeur maximum du temps de vol en altitude des suites de Syracuse pour \(n = 1\) jusqu’à \(n = 9999\).

Informations complémentaires

Python permet de retourner plusieurs valeurs simultanément. L’explication détaillée sera abordée dans le chapitre sur les tuples.

Par exemple, on peut définir une fonction qui retourne le carré et le cube d’un nombre entier :

• la définition de la fonction :

        def square_and_cube(n):
                return n**2, n**3

• son appel :

        x, y = square_and_cube(3)