Dans cette partie, on s’occupera essentiellement d’algorithmes
itératifs bas niveau. On utilisera des types de données simples (des
nombres entiers stockés dans des listes, et les structures de contrôle
de base (if, while, for).
Les fonctions haut niveau de Python (min(),
max(), mean(), sort(), etc. )
sont proscrites.
Créer un fichier python-06-listes-algo.py.
Selon la convention de structuration des modules, ce fichier sera structuré en quatre parties :
L’objectif est d’écrire les algorithmes ci dessous en mettant en place une méthodologie de résolution, c’est à dire en les structurant en 4 étapes fondamentales, permettant de préciser :
k à un problème résolu de taille k+1 (la
taille de la partie résolue augmente). Le problème non résolu passe lui
d’une taille n-k à une taille n-k-1 (la taille
de la partie non résolue diminue).Définir une fonction mini() qui :
L ;Ce premier exercice est entièrement corrigé.
On considère une liste L de n éléments
:

Si on souhaite concevoir l’algorithme retournant la valeur minimale
d’une liste L, on peut procéder comme suit.
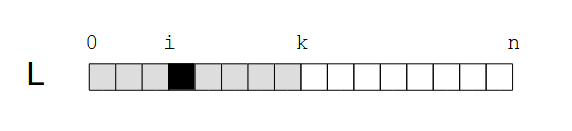
On commence par définir l’invariant de boucle qui consiste à écrire
que le problème est résolu au rang k si :
L[0:k] est la partie de la liste déja traitée ;L[k:n] est la partie de la liste restant à traiter
;L[i] est la valeur minimum de la liste
L[0:k] ;On peut exprimer cet invariant par la propriété suivante. Deux paramètres sont nécessaires pour définir cette propriété (un paramètre est une grandeur susceptible de prendre différentes valeurs au cours de l’exécution de l’algorithme) :
La propriété invariante décrit un problème résolu au rang
k.
I(i, k)<=>L[i]est la valeur minimum de la listeL[0:k]
L’invariant de boucle doit être vérifié avant l’entrée dans la
boucle. On cherche donc les valeurs initiales de i et
k qui assurent que I(i, k) est vraie AVANT de
commencer à résoudre effectivement le problème.
Manifestement, I(0, 1) est vraie avant l’entrée dans la
boucle. En effet, quelque soit la liste L,
L[0] est la valeur minimum de la liste L[0:1].
Donc :
i = 0 ;k = 1.L’étape suivante consiste à définir la condition de continuation.
Cette condition concerne le paramètre k qui mesure la
taille du problème résolu. Le problème sera complètement résolu lorsque
la totalité de la liste aura été parcourue (condition d’arrêt). La
condition de continuation est sa négation :
k < n
La dernière étape consiste à définir la progression.
Cette progression permet de passer d’un problème résolu de taille
k à un problème résolu de taille k+1. Sous la
condition C(k, n), on examine la valeur de L[k]. Si
L[k] est inférieur à L[i], alors
L[k] est la nouvelle valeur minimum de la liste
L[0:k+1]. On peut donc écrire :
L(k) < L[i], L[k] est la nouvelle
valeur minimale de L[0:k+1], ce qui se traduit par la
propriété I(k, k+1). En faisant i = k et
k = k+1, on rétablit I(i, k) ;L[i] reste la valeur minimale de
L[0:k+1], ce qui se traduit par la propriété
I(i, k+1). En faisant k = k+1, on rétablit
I(i, k) ;On obtient le code Python (naïf) de l’algorithme par transposition directe des étapes 2, 3 et 4 de la structuration du problème.
Vérifier la validité de la solution implémentée en faisant un appel à
mini() sur quelques listes à partir de main()
et en affichant/vérifiant la valeur de retour correspondante.
Exemple : si
L = [33, 36, 27, 15, 43, 35, 36, 42, 49, 21],
mini(L) retourne 15.
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Décrire les 4 étapes de l’algorithme permettant de retourner la
valeur maximale d’une liste d’entiers L.
Écrire la fonction maxi() correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
maxi() sur quelques listes à partir de main()
et en affichant/vérifiant la valeur de retour correspondante.
Exemple : si
L = [33, 36, 27, 15, 43, 35, 36, 42, 49, 21],
maxi(L) retourne 49.
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Décrire les 4 étapes de l’algorithme permettant de retourner l’index
correspondant à la valeur minimale d’une liste d’entiers
L.
Écrire la fonction ind_mini(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
ind_mini() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple : si
L = [33, 36, 27, 15, 43, 35, 36, 42, 49, 21],
ind_mini(L) retourne 3.
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Décrire les 4 étapes de l’algorithme permettant de retourner l’index
correspondant à la valeur maximale d’une liste d’entiers
L.
Écrire la fonction ind_maxi() correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
ind_maxi() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple : si
L = [33, 36, 27, 15, 43, 35, 36, 42, 49, 21],
ind_maxi(L) retourne 8.
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Décrire les 4 étapes de l’algorithme permettant de retourner la somme
des éléments d’une liste d’entiers L.
Écrire la fonction somme() correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
somme() sur quelques listes à partir de main()
et en affichant/vérifiant la valeur de retour correspondante.
Exemple : si
L = [33, 36, 27, 15, 43, 35, 36, 42, 49, 21],
somme(L) retourne 337.
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Décrire les 4 étapes de l’algorithme permettant de retourner la
moyenne des éléments d’une liste d’entiers L.
Écrire la fonction moyenne(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
moyenne() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple : si
L = [33, 36, 27, 15, 43, 35, 36, 42, 49, 21],
moyenne(L) retourne 33.7.
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Décrire les 4 étapes de l’algorithme permettant de retourner
retournant 1 si la L est croissante, -1 si L
est décroissante, et 0 sinon.
Ecrire la fonction est_trie(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
est_trie() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple 1 : si
L = [33, 36, 27, 15, 43, 35, 36, 42, 49, 21],
est_trie(L) retourne 0. Exemple 2 : si
L = [15, 21, 27, 33, 35, 36, 36, 42, 43, 49],
est_trie(L) retourne 1. Exemple 3 : si
L = [49, 43, 42, 36, 36, 35, 33, 27, 21, 15]
est_trie(L) retourne -1.
Ajouter une docstring et des doctest. Vérifier que les tests passent.
On considère une liste L de n entiers. On
veut calculer les indices d et f tels que
L[d:f] soit la première plus longue sous liste constante.
On veut une solution où la liste ne soit parcourue qu’une seule
fois.
Décrire les 4 étapes de l’algorithme permettant de retourner
d et f.
Ecrire la fonction pplslc(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
pplslc() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple : la première plus longue sous liste constante de
L = [2, 1, 1, 3, 4, 4] est L[1:3] = [1, 1].
Dans ce cas, pplslc(L) retourne (1, 3).
Ajouter une docstring et des doctest. Vérifier que les tests passent.
On considère une liste L de n entiers.
Écrire une fonction doublons(L) qui retourne la liste des
éléments qui apparaissent au moins deux fois.
Décrire les 4 étapes de l’algorithme permettant de retourner la liste des éléments qui apparaissent au moins deux fois. Jusqu’ici, les exercices ont été résolus en stockant en mémoire uniquement 1 ou 2 entiers. Ici, on peut utiliser des structures de données additionnelles.
Réfléchir au problème si la liste de départ est déjà triée (en ordre croissant par exemple).
Une fois ce problème résolu, réfléchir au problème si la liste de départ n’est pas triée.
Ecrire la fonction doublons(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
doublons() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple : on considère la liste L = [2, 1, 1, 3, 4, 4]..
doublons(L) retourne [1, 4].
Ajouter une docstring et des doctest. Vérifier que les tests passent.
On considère deux listes L1 et L2 de
n et m entiers. Écrire une fonction
elts_communs(L1, L2) qui prend les deux listes d’entiers
L1 et L2 en entrée et retourne une liste
contenant les éléments communs aux deux listes.
Décrire les 4 étapes de l’algorithme permettant de retourner la liste contenant les éléments communs aux deux listes.
Réfléchir au problème si les listes de départ sont déjà triées (en ordre croissant par exemple).
Une fois ce problème résolu, réfléchir au problème si les listes de départ ne sont pas triées.
Ecrire la fonction elts_communs(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
elts_communs() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple : on considère les listes
L1 = [2, 1, 1, 3, 4, 4] et
L2 = [ 5, 1, 6, 4, 1]. elts_communs(L1, L2)
retourne [1, 4].
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Écrire une fonction elts_differents(L1, L2) qui prend
deux listes d’entiers L1 et L2 en entrée et
retourne une liste contenant les éléments qui n’appartiennent qu’à une
seule des deux listes.
Décrire les 4 étapes de l’algorithme permettant de retourner la liste contenant les éléments qui n’appartiennent qu’à une seule des deux listes.
Réfléchir au problème si les listes de départ sont déjà triées (en ordre croissant par exemple).
Une fois ce problème résolu, réfléchir au problème si les listes de départ ne sont pas triées.
Ecrire la fonction elts_differents(L)
correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
elts_differents() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple : on considère les listes
L1 = [2, 1, 1, 3, 4, 4] et
L2 = [ 5, 1, 6, 4, 1]. elts_differents(L1, L2)
retourne [2, 3, 5, 6].
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Écrire une fonction pplsltc(L) qui prend une liste
d’entiers L en entrée et retourne les indices
d et f de début et de fin de la plus longue
sous-séquence de la liste où les éléments sont triés en ordre
croissant.
Décrire les 4 étapes de l’algorithme permettant de retourner les
indices d et f.
Réfléchir au problème si les listes de départ sont déjà triées (en ordre croissant par exemple).
Une fois ce problème résolu, réfléchir au problème si les listes de départ ne sont pas triées.
Ecrire la fonction pplsltc(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
pplsltc() sur quelques listes à partir de
main() et en affichant/vérifiant la valeur de retour
correspondante.
Exemple : on considère la liste
L = [ 33, 36, 27, 15, 43, 35, 36, 42, 49, 21] ,
pplsltc(L1, L2) retourne (5,9).
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Écrire une fonction np(L) qui prend en argument une
liste L de n entiers (négatifs et positifs),
calcule une permutation de L telle que L[0:p]
ne contient que des valeurs négatives, L[p:n] ne contient
que des valeurs positives ou nulles, et retourne l’indice
p.
Décrire les 4 étapes de l’algorithme permettant de retourner l’indice
p.
Cet algorithme ne met pas en oeuvre de structure de données supplémentaires. Il faut procéder par permutation des éléments.
Ecrire la fonction np(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
np() sur quelques listes à partir de main() et
en affichant/vérifiant la valeur de retour correspondante.
Exemple : on considère la liste
L = [7, -3, 3, 1, 4, -8, 3, -6, -5, 9] , np(L)
calcule la permutation [-3, -8, -6, -5, 4, 7, 3, 3, 1, 9 ]
et retourne p = 4.
Ajouter une docstring et des doctest. Vérifier que les tests passent.
Écrire une fonction pslsm(L) qui prend en argument une
liste L de n entiers (négatifs et positifs),
et retourne les indices d et f de début et de
fin de la première sous liste de somme maximum, ainsi que la somme
s des éléments de L[d:f].
Décrire les 4 étapes de l’algorithme permettant de retourner les
indices d et f et la somme s.
On peut penser à définir l’invariant
I(d, f, s, dp, i, sp)tel que :L[d:f]de sommesest la première sous liste de somme maximum deL[0:i];L[dp:i]de sommespest le suffixe de somme maximum.
Ecrire la fonction pslsm(L) correspondante.
Vérifier la validité de la solution implémentée en faisant un appel à
pslsm() sur quelques listes à partir de main()
et en affichant/vérifiant la valeur de retour correspondante.
Exemple : on considère la liste
L = [-1, 2, 1, -4, 3, 4, -6, 2, 3, 2, -3,1 ] ,
pslsm(L) retourne d = 4, f = 10
et s = 8.
Ajouter une docstring et des doctest. Vérifier que les tests passent.