6. Les séquences

Python propose une grande variété de structures de données. Parmi celles ci, on trouve des séquences, c’est à dire des structures de données ordonnées. Elles peuvent se décomposer par type.

6.1. Container sequences

Ce type de container permet de stocker de façon ordonnée les références des objets (de n’importe quel type) qu’elles contiennent. list, tuple et collections.deque sont des containers de type sequence.

6.1.1. Flat sequences

Une flat séquence stocke directement en mémoire la valeur de chaque item qui la compose. Les flat sequences sont plus compactes mais ne peuvent stocker que des types « primitifs » : caractères alphanumériques, octets, nombres.

str, bytes, bytearray, array.array et memoryview sont des flat sequences.

Les séquences peuvent également s’organiser en deux autres familles, selon qu’elles sont mutables ou pas.

6.1.2. Immutable sequences

Une séquence immutable est une séquence qui ne peut pas être modifiée une fois créée. On connait déjà les classes str et tuple. La classe bytes est également une séquence immutable.

Un exemple de manipulation d’une sequence immutable à partir des méthodes de base de la classe str

>>> s = "abc"
>>> s.__len__()
3
>>> s.__contains__('a')
True

La plupart de ces méthodes sont appelées par les fonctions builtin correspondantes. C’est cette dernière façon de faire que l’on va privilégier:

>>> len(s)
3
>>> 'a' in s
True

On peut construire un itérateur sur une séquence:

>>> i = s.__iter__()
>>> i.__next__()
'a'
>>> i.__next__()
'b'
>>> i.__next__()
'c'
>>> i.__next__()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
StopIteration

Généralement, itérer sur une séquence complète se fait à partir de la construction for in:

>>> a = "abc"
>>> for c in a:
...     print(c)
...
a
b
c

Les séquences disposent d’accesseurs bas niveau:

>>> s.__getitem__(0)
'a'

Ceux ci sont mis en oeuvre avec la syntaxe [ ]:

>>> s[0]
'a'

Comme on vient de le voir, les méthodes bas niveau n’ont pas vocation à être utilisées directement lorsque l’on travaille avec les séquences incluses dans la bibliothèque Python. Par contre, ces méthodes doivent être implémentées lorsque l’on développe ses propres classes séquences.

On dispose également d’autres méthodes de séquences permettant d’obtenir l’index ou le nombre d’occurrence d’un élément de la séquence:

>>> s.index('b')
1
>>> s.count('b')
1

6.1.3. Mutable sequences

Dans le cas de séquence mutables, on peut modifier la séquence une fois créee. La séquence mutable la plus courante est la classe list.

bytearray, array.array, collections.deque, memoryview sont également des séquences mutables.

Le diagramme de classes ci dessous permet de structurer les choses. Les noms en italique sont des classes et des méthodes abstraites.

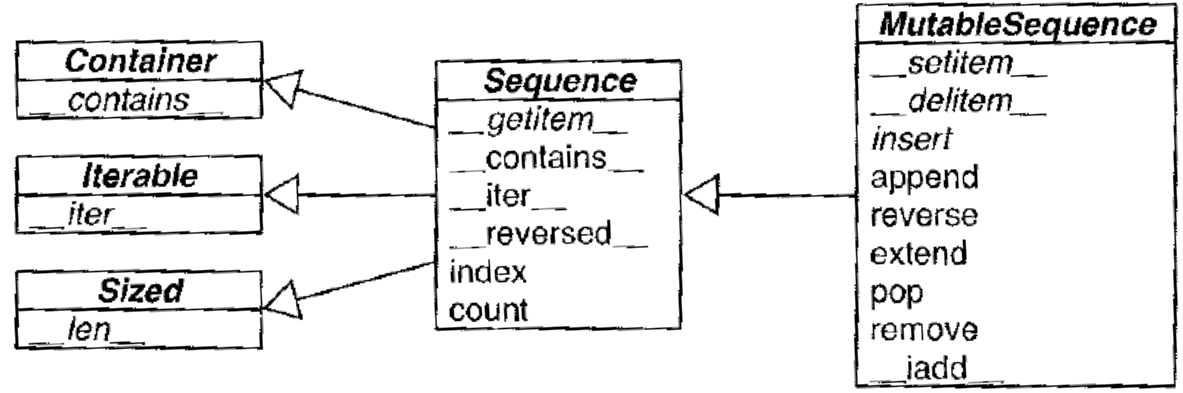
Comme toutes les séquences mutables, une liste dispose de toutes les méthodes des sequences immutables, mais du fait de sa mutabilité, d’autres sont disponibles. Construisons une simple liste:

>>> l = list(range(5))
>>> l
[0, 1, 2, 3, 4]

Elle dispose bien des méthodes de séquence immutable vues au paragraphe précédent:

>>> l.__contains__(1)
True
>>> l.__contains__(10)
False

Mais elle dispose en plus de méthodes permettant de modifier la structure de la liste.

En ajoutant des éléments:

>>> l.append(5)
>>> l.reverse()
>>> l
[5, 4, 3, 2, 1, 0]
>>> l.extend(list(range(10,13)))
>>> l
[5, 4, 3, 2, 1, 0, 10, 11, 12]

Ou en en retirant:

>>> l.pop()
12
>>> l
[5, 4, 3, 2, 1, 0, 10, 11]
>>> l.remove(3)
>>> l
[5, 4, 2, 1, 0, 10, 11]

6.2. Les list comprehension

La list comprehension est une façon élégante et concise de construire une liste:

>>> l = [ ord(c) for c in 'abcde' ]
>>> l
[97, 98, 99, 100, 101]

On peut inclure un prédicat simple:

>>> l = [ chr(i) for i in range(73,83) if i%2==0 ]
>>> l
['J', 'L', 'N', 'P', 'R']

ou plus complexe avec une clause else:

>>> l = [ chr(i) if chr(i).isalpha() else 'NA' for i in range(89,99) ]
>>> l
['Y', 'Z', 'NA', 'NA', 'NA', 'NA', 'NA', 'NA', 'a', 'b']

On notera que le prédicat se trouve ici avant la boucle for, ce qui n’est pas autorisé lorsque la clause else est absente:

>>> l = [ chr(i) if chr(i).isalpha() for i in range(73,83) ]
  File "<stdin>", line 1
    l = [ chr(i) if chr(i).isalpha() for i in range(73,83) ]

On peut également imbriquer plusieurs boucles:

>>> l = [ "".join((chr(i),str(j))) for i in range(65,73) for j in range(1,9) ]
>>> l
['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8', 'B1', 'B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B8', 'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'D1', 'D2', 'D3', 'D4', 'D5', 'D6', 'D7', 'D8', 'E1', 'E2', 'E3', 'E4', 'E5', 'E6', 'E7', 'E8', 'F1', 'F2', 'F3', 'F4', 'F5', 'F6', 'F7', 'F8', 'G1', 'G2', 'G3', 'G4', 'G5', 'G6', 'G7', 'G8', 'H1', 'H2', 'H3', 'H4', 'H5', 'H6', 'H7', 'H8']

On peut construire des listes de listes:

>>> l = [ [ "".join((chr(i),str(j))) for i in range(65,73) ] for j in range(1,9) ]
>>> l
[['A1', 'B1', 'C1', 'D1', 'E1', 'F1', 'G1', 'H1'], ['A2', 'B2', 'C2', 'D2', 'E2', 'F2', 'G2', 'H2'], ['A3', 'B3', 'C3', 'D3', 'E3', 'F3', 'G3', 'H3'], ['A4', 'B4', 'C4', 'D4', 'E4', 'F4', 'G4', 'H4'], ['A5', 'B5', 'C5', 'D5', 'E5', 'F5', 'G5', 'H5'], ['A6', 'B6', 'C6', 'D6', 'E6', 'F6', 'G6', 'H6'], ['A7', 'B7', 'C7', 'D7', 'E7', 'F7', 'G7', 'H7'], ['A8', 'B8', 'C8', 'D8', 'E8', 'F8', 'G8', 'H8']]

Exercice

Essayer de prédire le résultats des listcomps suivantes:

>>> l = [i*2 for i in [j+1 for j in range(20) if (j%3)==0] if i*i>19]

>>> strings = [ ['par', 'pare', 'pares'], ['se', 'sel', 'self'], ['a', 'an', 'arc'] ]
>>> l = [ (lettre, i) for i, l in enumerate(strings) for mot in l if len(mot)>3 for lettre in mot]

6.2.1. Performances

Une listcomp est une façon très élégante de construire une liste mais c’est également plus rapide qu’une boucle for classique. Une façon simple de mesurer les performances d’un code Python consiste à utiliser la classe timeit.timeit:

>>> import timeit
>>> timeit.timeit('[i for i in range(int(1e6))]', number=10)
1.195560211038753

On observe ici que remplir une liste avec un million d’entiers nécessite environ 1.2 s avec une listcomp (les performances peuvent varier avec la machine).

Avec une boucle for classique:

>>> LOOP = '''
... l = []
... for i in range(int(1e6)):
...     l.append(i)
... '''

>>> timeit.timeit(LOOP, number=10)
2.153525936214919

On constate ici que le temps d’exécution d’une boucle for classique est doublé !

Ce genre d’optimisation est fondamentale lorsque l’on manipule un grand nombre de données.

6.3. Les générateurs

Les générateurs sont une alternative intéressante aux listes, en ce sens qu’ils ne construisent pas la structure de données a priori mais fournissent les items à la demande. Pour effectuer la même tâche que précédemment, on définit une fonction générateur, où le mot clé return est remplacé par yield:

>>> def gen(n):
...     for i in range(n):
...             yield i
...

On fabrique un générateur avec gen() en précisant sa taille en argument:

>>> g = gen(int(1e6))
>>> g
<generator object gen at 0x0000020BAE4EECA8>

On accède à chacun des éléments en itérant sur le générateur

>>> for i in g: print(i)
...
0
1
2
3
...
999999

Tout se passe comme pour les listes à la différence majeure de la place occupée en mémoire. La liste est entièrement construite a priori:

>>> l = [i for i in range(int(1e6)) ]
>>> import sys
>>> sys.getsizeof(l)
8697464

Une liste d’un million d’entiers occupe 8.7 Mb en mémoire.

A contrario, un générateur délivre les éléments un par un et occupe très peu de place en mémoire:

>>> sys.getsizeof(g)
88

Avec le temps d’exécution, la réduction de l’occupation mémoire est un enjeu majeur lorsqu’on manipule un grand nombre de données.

6.3.1. Les gencomps

Comme pour les listes avec les listcomp, Python propose une syntaxe compacte pour fabriquer les générateurs, les gencomp. L’opérateur ( ) remplace l’opérateur [ ]:

>>> g = ( i for i in range(int(1e6)) )
>>> g
<generator object <genexpr> at 0x0000020BAE37D728>
>>> sys.getsizeof(g)
88

Le fonctionnement est transparent:

>>> for i in g: print(i)
...
0
1
2
3
...
999999

6.4. Les arrays

L’objet array.array est une séquence permettant de stocker de façon ordonnée et compacte les valeurs « primitives » : entiers, nombre flottants et caractères. Il diffère de la liste par le fait qu’il ne peut stocker que des valeurs primitives et aucun autre objet. Il en résulte un stockage en mémoire plus efficace que pour la liste. En effet, par construction cette dernière peut stocker des éléments inhomogènes (des objets de différente nature), ce qui a un impact sur l’utilisation de la mémoire. On réservera donc la liste pour le stockage d’une quantité réduite d’objets.

Le constructeur nécessite le type des éléments stockés et la séquence. Ici, les éléments sont stockés sous forme d’entiers. C’est le sens du premier argument I du constructeur. Le second est une séquence contenant les valeurs à stocker dans l”array:

>>> import array
>>> a = array.array('I', [ i for i in range(int(1e6)) ])
>>> type(a)
<class 'array.array'>

Après création, les attributs et les méthodes de la classe array.array permettent d’obtenir des informations élémentaires sur la structure de données:

>>> a.itemsize
4
>>> a.buffer_info()
(2249228529728, 1000000)

L’occupation mémoire est obtenue avec:

>>> a.buffer_info()[1] * a.itemsize
4000000

sys.getsizeof() donne une information légèrement différente.

Avertissement

getsizeof() calls the object’s __sizeof__() method and adds an additional garbage collector overhead if the object is managed by the garbage collector

>>> sys.getsizeof(a)
4000064

6.5. Les slices

Une caractéristique des séquences de Python est qu’elles peuvent être slicées. La syntaxe retenue est seq[i:j:k] où i est l’index de début (compris), j l’index de fin (non compris) et k le step. Si la valeur est manquante, une valeur par défaut est utilisée.

Cette convention présente plusieurs avantages (voir l’article de Dijkstra). Elle permet en particulier:

d’écrire seq = seq[:n] + seq[n:]
et d’obtenir explicitement le nombre j-i d’éléments de la séquence seq[i:j].

En Python, tout est objet, et les slices n’échappent pas à la règle. On considère les données INSEE du chomage en Ile de france pour l’année 2016:

>>> data ='''
... Période     75         77        78        91        92         93         94         95
... 2016M01     201 160    97 090    91 990    86 190    114 340    165 810    106 260    101 810
... 2016M02     200 660    97 110    92 790    86 040    114 360    165 580    106 120    101 810
... 2016M03     200 520    97 210    93 050    85 960    114 110    165 400    105 820    102 160
... 2016M04     198 750    96 290    92 280    85 240    112 780    163 700    104 890    100 980
... 2016M05     199 590    96 970    93 060    86 030    113 270    164 860    105 440    101 530
... 2016M06     199 500    97 190    93 440    85 870    112 980    164 990    105 580    101 740
... 2016M07     200 160    97 160    93 590    86 340    113 070    165 180    105 790    101 630
... 2016M08     201 740    98 420    94 980    87 660    113 760    166 200    106 910    102 610
... 2016M09     200 730    97 640    93 620    86 440    113 140    165 330    106 190    101 840
... 2016M10     200 130    97 460    93 030    86 600    112 580    164 830    105 930    101 120
... 2016M11     200 270    97 900    93 390    86 870    112 620    165 000    106 070    100 810
... 2016M12     200 150    97 960    93 730    87 140    112 620    164 520    106 020    101 440
... '''

>>> lines = data.split('\n')[2:-1]

>>> lines[0]
'2016M01     201 160    97 090    91 990    86 190    114 340    165 810    106 260    101 810'

On peut accéder aux statistiques par département en slicant chaque ligne. Pour Paris

>>> for l in lines:
...     print(l[12:19])
...
160
660
520
750
590
500
160
740
730
130
270
150

Cette syntaxe est peu lisible. Utiliser les objets slice donne un code plus lisible:

>>> ESSONNE = slice(43,49)
>>> ESSONNE.start
43
>>> ESSONNE.stop
49

>>> for l in lines:
...     print(l[ESSONNE])
...
86 190
86 040
85 960
85 240
86 030
85 870
86 340
87 660
86 440
86 600
86 870
87 140

6.6. Les tris

Python propose deux façons de trier les séquences, en utilisant l’algorithme TimSort, un mix des algorithmes Merge Sort et Insertion Sort. Si vous souhaitez vous rafraîchir la mémoire sur les différents algorithmes de tri, vous pouvez consulter les ressources suivantes:

https://www.toptal.com/developers/sorting-algorithms rappelle le fonctionnement, la complexité des principaux algorithmes, ainsi que le type de problèmes pour lesquels ils fournissent une réponse pertinente.
https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html propose une animation visuelle paramétrable.
http://sorting.at/ présente graphiquement un fonctionnement détaillé.

Pour ce qui concerne la complexité algorithmique, le TimSort a l’avantage d’être très rapide sur les séquences déjà un peu ordonnées. Le pire cas est en \(\Theta(n \log n )\) alors qu’il est en \(\Theta(n^2)\) pour le QuickSort.

6.6.1. `list.sort()`

La première façon de trier une séquence est la méthode list.sort() qui trie « sur place » une liste. C’est à dire qu’elle modifie l’objet list et ne retourne rien (ou plus exactement elle retourne l’objet None):

>>> l = [5, 2, 3, 1, 4]
>>> x = l.sort()
>>> x is None
True
>>> l
[1, 2, 3, 4, 5]

Important

Le fait que list.sort() retourne None est une convention en Python, utilisée chaque fois qu’une méthode ou une fonction modifie un objet « sur place ».

6.6.2. `sorted()`

La seconde façon de faire est d’utiliser la fonction sorted() qui accepte en paramètre un iterable au sens large (pas uniquement une liste). Cette fonction retourne une liste (quel que soit le type d’iterable passé en paramètre):

>>> l = [5, 2, 3, 1, 4]
>>> sl = sorted(a)
>>> l
[5, 2, 3, 1, 4]
>>> sl
[1, 2, 3, 4, 5]

>>> t = (5, 2, 3, 1, 4)
>>> type(t)
<class 'tuple'>
>>> st = sorted(b)
>>> type(st)
<class 'list'>
>>> st
[1, 2, 3, 4, 5]

La fonction sorted() accepte tout type d’iterable. Pour un dictionnaire, les éléments triés sont les clés:

>>> d = {1: 'D', 2: 'B', 3: 'B', 4: 'E', 5: 'A'}
>>> type(d)
<class 'dict'>
>>> sorted(d)
[1, 2, 3, 4, 5]

6.6.3. La clé de tri

La méthode list.sort() et la fonction sorted() ont toutes les deux un paramètre key optionnel permettant d’appliquer une fonction à l’item à trier avant d’effectuer le tri proprement dit. Si le paramètre key n’est pas fourni, la fonction identité est utilisée:

>>> pc = "paresse orgueil gourmandise luxure avarice colère envie".split()
>>> sorted(pc)
['avarice', 'colère', 'envie', 'gourmandise', 'luxure', 'orgueil', 'paresse']
>>> sorted(pc, key=None)
['avarice', 'colère', 'envie', 'gourmandise', 'luxure', 'orgueil', 'paresse']

Le tri utilisé dépend de la nature des items dans l’itérable. Lorsque ce sont des str, l’ordre lexicographique est utilisé:

>>> sorted(['Port', 'portée', 'Porté', 'porte'])
['Port', 'Porté', 'porte', 'portée']

Utiliser une clé de tri, permet de passer l’item à trier en paramètre d’une fonction et d’utiliser sa valeur de retour plutôt que l’item lui même:

>>> sorted(pc, key=len)
['envie', 'luxure', 'colère', 'paresse', 'orgueil', 'avarice', 'gourmandise']

On peut également écrire sa propre fonction et l’utiliser comme clé de tri:

>>> def value(name):
...     return sum([ord(letter) - 96 for letter in name])
...

>>> sorted(pc, key=value)
['envie', 'avarice', 'paresse', 'orgueil', 'luxure', 'gourmandise', 'colère']

>>> value('colère')
189
>>> value('envie')
55

6.6.4. Tris de structures complexes

Le tri peut s’appliquer à des séquences non flat, c’est à dire des séquences contenant des objets non primitifs:

>>> philosophers = []
>>> philosophers.append( ('Baruch', 'Spinoza', 1632, 10) )
>>> philosophers.append( ('Blaise', 'Pascal', 1623, 11) )
>>> philosophers.append( ('Emmanuel', 'Kant', 1724, 13) )
>>> philosophers.append( ('Friederich', 'Nietzsche', 1844, 14) )

Si aucune clé de tri n’est fournie, le premier élément de la structure à trier (ici le prénom) est utilisé par défaut:

>>> sorted(philosophers)
[('Baruch', 'Spinoza', 1632, 10), ('Blaise', 'Pascal', 1623, 11), ('Emmanuel', 'Kant', 1724, 13), ('Friederich', 'Nietzsche', 1844, 14)]

Plutôt que de définir explicitement une fonction à usage unique, on peut utiliser les lambda functions comme clé de tri. Cet équivalent des fonctions anonymes dans d’autres langages permet d’écrire un code compact. On y reviendra plus loin dans le paragraphe Les lambda fonctions.

On peut trier sur l’année de naissance:

>>> sorted(philosophers, key= lambda x:x[2])
[('Blaise', 'Pascal', 1623, 11), ('Baruch', 'Spinoza', 1632, 10), ('Emmanuel', 'Kant', 1724, 13), ('Friederich', 'Nietzsche', 1844, 14)]

ou sur le nom de famille:

>>> sorted(philosophers, key= lambda x:x[1])
[('Emmanuel', 'Kant', 1724, 13), ('Friederich', 'Nietzsche', 1844, 14), ('Blaise', 'Pascal', 1623, 11), ('Baruch', 'Spinoza', 1632, 10)]

ou bien encore sur le nombre d’oeuvres principales (bien qu’en philosophie, ce soit une métrique tout à fait discutable):

>>> sorted(philosophers, key= lambda x:x[3])
[('Baruch', 'Spinoza', 1632, 10), ('Blaise', 'Pascal', 1623, 11), ('Emmanuel', 'Kant', 1724, 13), ('Friederich', 'Nietzsche', 1844, 14)]

Il peut arriver de trouver des valeurs égales, et l’ordre des items de même rang est alors déterminé par une clé de tri secondaire. Lorsqu’elle n’est pas explicitement précisée, le premier élément de l’item est utilisé

>>> philosophers.append( ('Jean-Jacques', 'Rousseau', 1712, 13) )
>>> sorted(philosophers, key= lambda x:x[3])
[... , ('Emmanuel', 'Kant', 1724, 13), ('Jean-Jacques', 'Rousseau', 1712, 13), ... ]

On peut également spécifier explicitement cette clé secondaire, en demandant à la lambda function de retourner un tuple dont le deuxième élément est alors la clé secondaire:

>>> sorted(philosophers, key= lambda x:(x[3], x[2]) )
[... , ('Jean-Jacques', 'Rousseau', 1712, 13), ('Emmanuel', 'Kant', 1724, 13), ...]

Astuce

Le recours au collections.namedtuple() permet d’accéder aux champs du tuple de façon plus lisible et plus explicite. Le tri par année de naissance pourrait ainsi s’écrire:

>>> from operator import attrgetter
>>> sorted(philosophers, key= attrgetter('birthyear') )

6.6.5. L’ordre de tri

Par défaut, l’ordre de tri est ascendant. Le paramètre reverse permet d’inverser cet ordre:

>>> sorted(philosophers, key= lambda x:x[2], reverse=True )
[('Friederich', 'Nietzsche', 1844, 14), ('Emmanuel', 'Kant', 1724, 13), ('Jean-Jacques', 'Rousseau', 1712, 13), ('Baruch', 'Spinoza', 1632, 10), ('Blaise', 'Pascal', 1623, 11)]

Par contre, en cas de tri avec des clés multiples, l’ordre de tri est appliqué de façon globale au tuple retourné par la lambda fonction. On trie ici par nombre d’oeuvres décroissant puis par année décroissante:

>>> sorted(philosophers, key= lambda x:(x[3], x[2]), reverse = True )
[('Friederich', 'Nietzsche', 1844, 14), ('Emmanuel', 'Kant', 1724, 13), ('Jean-Jacques', 'Rousseau', 1712, 13), ('Blaise', 'Pascal', 1623, 11), ('Baruch', 'Spinoza', 1632, 10)]

Pour trier par nombre d’oeuvres décroissant puis par année croissante, il faut modifier le tuple retourné par la lambda function:

>>> sorted(philosophers, key= lambda x:(x[3], -x[2]), reverse = True )
[('Friederich', 'Nietzsche', 1844, 14), ('Jean-Jacques', 'Rousseau', 1712, 13), ('Emmanuel', 'Kant', 1724, 13), ('Blaise', 'Pascal', 1623, 11), ('Baruch', 'Spinoza', 1632, 10)]

Exercice

Comme on vient de le voir, les tris s’effectuent avec l’ordre naturel lorsqu’il s’agit de nombres, et avec l’ordre lexicographique lorsqu’il s’agit de lettres. Il est cependant un cas où l’ordre lexicographique ne conduise pas à une solution pertinente. Considérons un répertoire contenant une liste de fichiers:

>>> files = [ 'f1.txt', 'f2.txt', 'f10.txt']

Dans ce cas, le tri lexicographique n’apporte pas une réponse adaptée:

>>> sorted(files)
['f1.txt', 'f10.txt', 'f2.txt']

La raison en est que les nombres utilisés dans les noms de fichier sont triés avec l’ordre lexicographique, pour lequel:

>>> '2' < '10'
False

Imaginer une fonction f() à passer au paramètre key permettant de résoudre ce problème, tel que:

>>> sorted(files, key=f)
['f1.txt', 'f2.txt', 'f10.txt']

6.7. Recherche dans une séquence

La recherche dans les séquences est un sujet majeur, avec un fort impact sur les temps de calcul. Les performances dépendent de la structure de donnée, du fait qu’elle soit triée ou pas.

On considère une liste de taille variable, constituée d’élément tirés au sort aléatoirement avec la fonction random.randrange(). Dans la liste, on effectue les opérations de recherche suivantes:

le premier élément
l’élément au milieu
le dernier élément
un élément qui n’est pas dans la liste

Le code ci dessous réalise cette opération et formate les résultats avec la méthode de chaine str.format().

import random, timeit

SETUP = '''
import random
from __main__ import l, x
'''

result = []

for SIZE in [10000, 100000, 1000000, 10000000]:
    res = [SIZE]
    l = [ random.randrange(SIZE*2) for i in range(SIZE) ]
    for x in [ l[0], l[SIZE//2], l[-1], -1 ]:
        res.append(timeit.timeit('x in l', number=10, setup=SETUP))
    result.append(res)

print("{:>10} - {:^12} - {:^12} - {:^12} - {:^12}".format("SIZE", "1st elt", "middle elt", "last elt", "not in list") )

for r in result:
    print("{:>10} - {:10.8f} s - {:10.8f} s - {:10.8f} s - {:10.8f} s".format(*r) )

L’utilisation du module random fait que les résultats ci dessous ne sont pas reproductible, mais la tendance observée l’est:

    SIZE -   1st elt    -  middle elt  -   last elt   - not in list
   10000 - 0.00000064 s - 0.00084703 s - 0.00141085 s - 0.00119405 s
  100000 - 0.00000096 s - 0.00779258 s - 0.01686130 s - 0.01206940 s
 1000000 - 0.00000096 s - 0.08067754 s - 0.15480338 s - 0.12854622 s
10000000 - 0.00000160 s - 0.81813380 s - 1.44595326 s - 1.29124449 s

On constate que le temps de recherche du premier élément est indépendant de la taille de la liste. Ce qui est logique puisqu’il s’agit du premier élément rencontré lors du parcours.

Le temps de recherche du dernier élément augmente de façon linéaire avec la taille de la liste. Logique également puisque la liste est parcourue en entier.

Le temps de recherche d’un élément n’appartenant pas à la liste est sensiblement le même que celui du dernier élément car il faut avoir parcouru la totalité de la liste pour statuer sur le fait que l’élément est présent ou non.

6.7.1. Recherche dans une séquence triée

Rechercher un élément dans une liste, triée ou non, peut se faire avec la méthode list.index() dont la complexité algorithmique est en \(\Theta(n)\):

>>> SETUP = '''
... from __main__ import l, SIZE
... '''

>>> SIZE = 1000000
>>> l = [ random.randrange(SIZE*2) for i in range(SIZE) ]
>>> l = sorted(l)

>>> timeit.timeit('l.index(l[SIZE//2])', number=10, setup=SETUP)
0.5671283348642646

Cependant lorsque la séquence est ordonnée, ce qui coûte \(\Theta(n \log n\)), la recherche avec la méthode list.index() n’est pas du tout efficace. On lui préférera l’algorithme binary search dont la complexité algorithmique est en \(\Theta(\log n)\):

>>> SETUP = '''
... import bisect
... from __main__ import l, SIZE
... '''

>>> timeit.timeit('bisect.bisect_left(l, l[SIZE//2])', number=10, setup=SETUP)
4.746681167944189e-05

Le module bisect propose également la fonction bisect.insort() qui permet d’insérer un élément dans la liste, tout en conservant son ordonnancement.

6.8. Piles et queues

La liste pourrait être un bon candidat pour implémenter une stack ou une queue en utilisant les méthodes list.append(), list.pop() et list.insert().

En utilisant list.append(), les performances algorithmiques sont correctes pour l’insertion « à droite »:

>>> import random, timeit
>>> SIZE = 1000000
>>> l = [ random.randrange(SIZE*2) for i in range(SIZE) ]

>>> SETUP = 'from __main__ import l'

>>> timeit.timeit('l.append(-1)', number=10, setup=SETUP) # insertion à droite
8.659485921214127e-06

mais ne sont pas du tout optimales pour ce qui concerne l’insertion « à gauche » qui nécessite list.insert():

>>> timeit.timeit('l.insert(0, -1)', number=10, setup=SETUP)
0.015554361045398798

Il existe une structure de données bien plus adaptée (car optimisée pour les opérations précédentes), la deque (double ended queue):

>>> from collections import deque
>>> SIZE = 1000000
>>> l = [ random.randrange(SIZE*2) for i in range(SIZE) ]
>>> d = deque(l)
>>> len(d)
1000000

L’insertion à droite est toujours aussi efficace:

>>> SETUP = 'from __main__ import d'

>>> timeit.timeit('d.append(-1)', number=10, setup=SETUP) # insertion à droite
1.3149589676686446e-05

mais maintenant l’insertion à gauche l’est tout autant:

>>> timeit.timeit('d.appendleft(-1)', number=10, setup=SETUP) # insertion à gauche
8.659485956741264e-06

Le choix de la structure de données est fondamental pour l’optimisation des performances.