MorphoGraph and Imagery - Practical session 3

from an original subject in French by Michel Couprie, Gilles Bertrand

Preliminaries

First of all, get the file graphestp3.tar.gz and uncompress it :

    gunzip graphestp3.tar.gz
    tar xvf graphestp3.tar
    rm graphestp3.tar
    cd GraphesTp3; ls

This archive contains C programs for manipulating graphs. Documentation of these programs can be found here:

Reminder on the two first practical sessions: description of the data structures used to represent a graph by Γ (its successors map). Also remind to refer to the documentation of the source code, including:

• source of the definition of the main data structures (graphe, cell...)
• description of basic functions to handle graphs (see in particular AjouteArc -meaning AddArc in French -, EstSuccesseur - meaning IsSuccessor in French)
• description of the functions to handle lists (LIFO) and Boolean arrays (see in particular CreeLifoVide - meaning CreateEmptyLifo in French-, EnsembleVide - meaning EmptySet in French)

A journey in the metro

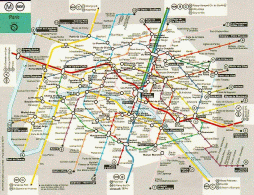
The RATP (public transportation company in Paris) provides its users with an interactive service that finds the shortest route between two subway stations chosen by the user. Our goal in this session is the design and development of a simplified version of such software. We will also consider the most effective strategies to solve problems of the same type.

0. The data

You will find in the file metro_complet.graph a network constructed as follows:

• Each vertex corresponds to a station for a given line (eg Republic [line 3] and Republic [line 5] are two distinct vertices).
• To each vertex is associated the position of a station on a map (scale: 1 ~ 25.7m).
• To each vertex is associated a station name (string).
• Two vertices form a directed arc if the associated stations are directly linked by metro (the graph is not symmetric because of some "one way" tunnels, for example around Porte d'Auteuil). This arc is weighted by the estimated time in seconds to travel from one station to the other (taking as a basis an average speed of 10m / s or 36km / h).
• Two vertices are linked to each other by two symmetric arcs if one can walk between the corresponding stations without buying a new ticket. These arcs are then weighted by an estimation of the average waiting and walking time (120s).

Visualize the graph of Paris metro, using the programs graphe2ps.exe and display:

    make graphe2ps.exe
    graphe2ps.exe metro_complet.graph
    display metro_complet.graph.eps

1. Dijkstra in the metro

Implement Dijkstra algorithm studied in course (see lecture 4, slide 15). Find below a short description of the requested function:

/* ====================================================================== */
/*! \fn void Dijkstra(graphe * g, int x)
    \param g (entrée) : a network. The length of each arc must be stored in
                        the field v_arc of the structure cell.
    \param x (entrée) : a vertex of g.
    \brief compute, for each vertex y of g, the length Dx(y)of a shortest path
           from x to y. This length is stored in the field 
           v_sommets of the structure g.
*/
/* ====================================================================== */

Test your program on a small graph of your choice (this one for instance), then on the graph of the metro.

Useful functions:

• EnsembleVide()
• The type of the values associated to the arcs and to the vertices is long (see definitions in graphes.h). We can use the constant LONG_MAX for infinity.

2. Shortest path

Implement an algorithm (based on the values returned by Dijkstra) for computing a shortest path from a vertex x to a vertex y. Find below a short description of the requested function:

/* ====================================================================== */
/*! \fn graphe * SP(graphe * g, int x, int y)
    \param g (entrée) : a network. The length of each arc must be stored in
                        the field v_arc of the structure cell.
    \param x (entrée) : a vertex of g (start).
    \param y (entrée) : a vertex of g (arrival).
    \return a shortest path from x to y in g.
    \brief returns a shortest path from x to y in g.
*/
/* ====================================================================== */

Computation time can be improved by terminating Dijkstra when the vertex y is reached.

Test your program on a small graph of your choice, then on the graph of the metro. Visualize (see EPSGraphe) the obtained shortest path for a few trips in the metro.

Useful functions:

• InitGraphe()
• Symetrique()
• AjouteArc()

3. Improvement of Dijkstra

In Dijkstra algorithm, the vertices of S\ can be divide into two subsets:

• Set T that contains the vertices of S whose current value is finite; and
• Set U that contains the vertices of S whose current value is infinite.

In the basic version of Dijkstra algorithm, we search for vertex of minimum value in [T union U]. The algorithm can be significantly improved by introducing a variable that represent the set T (as a list) in order to restrain the search to that set.

Implement this improvement and test it.

Useful data structures and functions found in the graphaux.h and graphaux.c files:

• ListeChainee, LCell, ListeVide(), ajouteElmt(), supprimeLCell(), afficheListe(), estListeVide()
• The usages of these functions can be found in the file graphaux.c
• An example of use of these data structures and functions is available in the file testeListeChainee.c

Bonus (homework to be done after the session)

4. Improving the estimation of the time of the journey

In the previous method, we do not take into account the time taken by the metro when it stops at a station. We would like to add to the estimation of the total time of the route an average waiting time of 20s for each stop. To this end, there exist two kinds of solutions:

• by modifying the network,
• by modifying the algorithm.

Explain how to proceed in each case (no implementation is required).

Acknowledgement

We thank RATP for the data available on its web site. We also thank L. Granboulan and L. Mauborgne from ENS, authors of a Practical Session on finding shortest path in the metro which inspired the subject of this practical session.