Figure 2.1: Factorization example
2.1 Specification of algorithm and model of factorized graph
Real-time embedded applications
Real time applications are mostly found in the domains of signal and image processing and process control under real-time constraints. They must permanently interact with their environment that they control. They react to input signals received from environment, by triggering computations to generate output reactions and/or change their internal state. In order to keep control over their environment, they have to react within bounded delays.
When the complexity of the application algorithm and the ratio between
its computation volume and the response time bound are high, standard off
the shelf sequential architectures are inadequate, and parallel multicomponent
hardware architectures are required. Programming such architectures is
an order of
magnitude harder than with mono-component sequential ones, and even
more when hardware resources must be minimized ti match cost, power and
volume constraints required for embedded applications.
The AAA methodology and the SynDEx CAD software that supports it, have
been developed to help designers in optimizing the implementations of such
applications.
AAA Methodology
AAA means Algorithm Architecture "Adequation". This methodology is supposed to find the best match between an algorithm and an architecture, considering the constraints. There is a difference in the meaning of Adequation in French and English. In French it means efficient and in English it means sufficient.
The AAA methodology is based on the graph models to exhibit both the
potential parallelism of the algorithm and the available parallelism of
the multicomponent. The implementation consist of distributing and scheduling
the algorithm data-flow graph on the multicomponent hyper-graph while satisfying
real-time constraints. This is formalized in terms of graphs transformations.Heuristics
are used to optimize real-time performances and resources allocation of
embedded
real-time applications.
The result of graphs transformations is an optimized Synchronized Distributed Executive (SynDEx), automatically build from a library of architecture dependent executive primitives composing the executive kernel. There is one executive kernel for each supported processor.
SynDEx CAD software
SynDEx is a graphical interactive software implementing the AAA methodology. It offers the following options:
Algorithm specification is the starting point for hardware implementation. In this specification the relation between the operations is only based upon their data dependency meaning that with this we show potential parallel operations.
This specification has to be independent of hardware implementation,
so it can be used by wide range of processors and/or reconfigurable circuits
( VHDL )
An algorithm is modeled by a dependence graph where each node models
an operation ( arithmetical, logical or more complex one) and each edge
model a data produced by node as an output ready to be used as input data
for other nodes. Some patterns are repeating themselves only using different
kind of data, so the factorization of the graph finds these repetitive
patterns and replace them by only one pattern, which is repeated as many
times as needed.
We will call this pattern frontier. You have two types of frontiers:
The process of factorization is applied to reduce the specification
size and to show which frontiers are repeating and it does not change dependencies
of the graph. You can see example of factorization on Figure
2.1. There under figure a) the DFG is presented ( data-flow graph ).
Then on figure b) is graph after factorization called factorized DFG (FDFG).
Under figure c) there is FDFG of operator V. You can see from this simple
example how can you reduce surface with factorization.
Figure 2.1: Factorization example
With factorization we got new graph called FDFG graph (graphe factorise de dependances de donnees - factorized data-flow graph, you can see the example of FDFG for product between matrix and vector on Figure 2.1 under b) and c) ) and special nodes are revealed.
Each node specifies different way of processing data that are crossing
the factorization frontier.
These nodes are:
Basic nodes
Basic nodes describes combinatorial operations of algorithm.
We distinguish between five types
Each one of these nodes specifies a different form of factorization of the arcs which are on the frontier
Nodes of infinite frontiers
Here you have the same nodes as in finite frontier: FORK infinite
, JOIN infinite, ITERATE infinite and DIFFUSION infinite. They have
the same entries and exits, delays and constants for data-flow graph. The
difference is shown when you want to make hardware implementation.
Hardware implementation consist of replacing each node of FDFG with
corresponding specification of operator ( written in VHDL ) and every arc
with connection between operators.
2.2.1 Operators of the infinite frontiers
If you want that your application interact with environment than you
connect your application with the environment through the operators of
infinite factorized frontiers. The nodes for interaction with environment
are the sensors ( FORK infinite ), which are input nodes of graph and actuators
(
JOIN infinite ), which are output nodes of graph, as well as delays
(ITERATE infinite) and/or constants of the data-flow graph (DIFFUSION infinite).
Operator FORK infinite : sensor
FORK infinite operator represents the sensor which translates analog signal into digital. This sensor includes all the necessary circuits for the conversion and sampling of the signals ( analog-to-digital converter and register ) as seen on the Figure 2.2
Figure 2.2: Operator FORK infinite
Operator JOIN infinite : actuator
JOIN infinite operator represents the actuator which converts digital signal into analog signal. This actuator includes all the necessary circuits for memorization and conversion of signal ( register and digital-to-analog converter) as seen on Figure 2.3.
Figure 2.3: Operator JOIN infinite
Operator ITERATE infinite : delay
ITERATE infinite operator corresponds to register as seen on Figure 2.4 . Register keeps the exit same during whole clock cycle and the value of the exit is the value which was on the entry at the end of previous clock cycle. En is signal which enables the register. With this signal active registers inputs are put to output, otherwise register keeps state. If the signal of initialization is present (rst), register is forced into the state init and compared to the ITERATE finite it doesn't have the fin exit, which presents us the end of iteration, so iteration is repeated infinitely.
Figure 2.4: Operator ITERATE infinite
Operator DIFFUSION infinite : constant
Implementation of DIFFUSION infinite is the same as the implementation
of DIFFUSION finite seen on Figure 2.9. It represent
the repetitive constant for the graph of data-flow
2.2.2 Operators of the finite frontiers
Graphs also contains finite frontiers. These frontiers are used to process data gathered by sensors and put the results into actuators.
Operator FORK
FORK is an operator which select from the input vector at the entry one element by the command signal and put it to the exit.As seen on Figure 2.5 b) it has:
i = (IN-OUT)/(f-1)
Parameter i tells us how many output vectors of OUT size do we have
to get from the IN size vector. For example: on Figure
2.6 you can see two cases in first we have the IN size of 6 and OUT
size of 2 and f is 3 so that makes i equals 2. In the second case we have
same example except the IN size is changed
to 4 and that makes i equals 1. In case that IN size equals OUT size
the FORK is transformed into DIFFUSE.
Figure 2.5: Operator FORK
Figure 2.6: Example of using operator FORK
Operator JOIN
JOIN is an operator opposite of FORK. It makes a vector at the exit
of elements at the entry (see Figure 2.7 ). It is
composed of d-1 registers which are selected by command and enable signals
and of IMPLODE operator, which composes the exit vector from each of registers
outputs. Only one of the registers is enabled at the same time. So
it take d times to have the correct vector at the
exit.
Figure 2.7: Operator JOIN
Operator ITERATE
Is the same as ITERATE infinite but it has also the fin output, which
signals the end of iteration. As seen on Figure 2.8
it has input signals of enable, clock, init, command,entry and output signal
exit and fin. At initialization phase the mux select the init value. After
the end of iteration (d-1) the signal fin
has the desired value. Operator ITERATE is composed of:
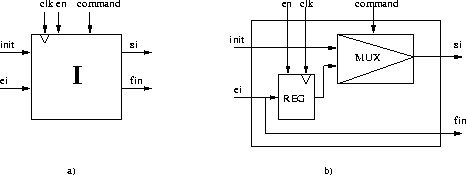
Figure 2.8: Operator ITERATE
Operator DIFFUSION
DIFFUSION is an operator which connects its inputs to output directly as seen on Figure 2.9 .
Figure 2.9: Operator DIFFUSION
Basic operators establish combinatorial part of algorithm specification.
Operator CONSTANTE
CONSTANT operator corresponds in hardware implementation to the operator
DATA.
This operator is used for example to provide initial value for operator
ITERATE.
Operator RESULTAT
Infinite factorized graphs can only have infinite results, factorized by operator JOIN infinite, so they can't have node RESULTAT.
Operator CALCUL
This operator is available in the library and it's implementation depends on which function we need to implement.
Operator IMPLODE
IMPLODE operator corresponds to regrupement of d input data into one
vector.
It implements direct connections between operators at entry side and
operators at exit side as seen on Figure 2.10.
Figure 2.10: Operator IMPLODE
Operator EXPLODE
EXPLODE operator corresponds to decomposition of data bus into d elements. It implements direct connections between operators at entry side and operators at exit side as seen on Figure 2.11.
Figure 2.11: Operator EXPLODE
2.3 Automatical synthesis of circuits
Automatical synthesis of circuits consist of automatical construction
of physical structure from behavioral representation on very high level,
which is for us factorized dependency graph. This synthesis considerably
reduce the time to develop the circuit and allow us to explore different
types of hardware implementations to obtain the best compromise between
surface and performance for
our application.
2.3.1 Rules for synthesis data path
The synthesis of data path consist of replacing each node with corresponding operator. Operator is combinatorial for a operation node or it consists of multiplexer and/or register for a frontier node (for more details see section 2.2).
Hardware implementation of dependencies between operators consists of
replacing each arc of graph with physical connection between corresponding
operators with operations. Operators and their interconnections makes a
data path of circuit.
2.3.2 Rules for synthesis control path
Control path has to be added to data path to control the data flow between the registers of operators and control the multiplexers. It is important for synchronized transfer between registers. For example on the Figure 2.12 you can see
Figure 2.12: Transfer of data between registers
what is control path used for. You have circuit made of register RegE,
combinatorial part X and register RegS. Both of the registers are controlled
by the clock (clk) signal. Each register reacts to the rising edge of the
clock signal. On the first rising edge of clk data Te is put into RegE.
This data is
then processed by combinatorial part X and output is stored in the
RegE at the next rising edge of clk. So the period of the clock has to
be greater than the latency of the combinatorial circuit X, in this case
the whole circuit produces right results. If circuit X contains some parts
which break up into identical
subparts, repeated regularly, these subparts can be factorized into
only one part surrounded by frontier operators, made of registers and multiplexers,
that control the iterative use of subpart. Therefor these new registers
must change state many times between the transition of RegE and RegS. These
registers will change state at every d times and not every clock cycle,
if the subpart is iterated d times. There are two conditions that has to
be met for the register to change state. First one is that data are stable
on the entries and second all of the consumers on the exit of the register
has to finish using previous data. If the data on upstream side came at
different propagation times there is need for a synchronized circuit. The
synchronization of circuit X can be achieved by using communication protocol
request/acknowledge as shown on Figure2.13.
Figure 2.13: Synchronized circuit
The data producers upstream of X ( Td1 and Td2 in Figure 2.13, d suffix means downstream) signal that data is available for X by driving a transition of request signal ( rd1 and rd2 ). X circuit will use this data if the ru is active.Circuit X signals its upstream producers that it has finished using data and that they can send new data by activating its au signal (au means acknowledge upstream) The same thinking is applied on the downstream side. The composition of many synchronized combinatorial circuit is also a synchronized combinatorial circuit.
Control unit
If X is sequential circuit ( containing registers ) as is the case
for circuit containing factorized parts and also containing factorization
operators, each factorized frontier has upstream and downstream relations
on both sides, "slow" and "fast". The relations between upstream/downstream
request/acknowledge
signals on both sides of the frontier makes up the "control unit" of
the factorized frontier as seen on Figure 2.14.
Figure 2.14: Control unit (finite)
This control unit contains a counter and additional logic to generate
the communication protocol between frontiers ( slow and fast, upstream
and downstream, request and acknowledge signals ), the counter value and
the enable signal, that control frontier operators. The enable signal (en)
determines the clock cycles of frontier operators registers ( F infinite,
J infinite, J and I) to change their state. If the enable signal is true
on the rising edge of clock, then the register can also change state. Otherwise
the registers output stays the same.
In the case of infinite frontier the control unit changes a little bit. Obviously there is no need for a counter, because the infinite frontier is repeated all the time, there is also no need for clock and reset signal. You can see the infinite control unit on the Figure 2.15.
Figure 2.15: Control unit (infinite)
The entries rsu and asd are always active ( rsu='1' and asd='1') because the data are produced and consumed all the time at the infinite border. There is no asu and rsd because there can't be any frontier on the slow side of infinite frontier.
Interconnection of control units
Control units can be automatically connected from the neighbourhood
graph. This graph shows us how are the frontiers interconnected. You can
see example of the frontier neighbourhood graph (FNG) on Figure 2.17. On
this graph nodes corresponds to control units of frontiers and arcs corresponds
to request signals transmitted between control units. Signals of acknowledge
are transmitted the opposite way of request signals, between all control
units. If there is more than one signal at the same entry there is a need
for conjunction on the entry. So we have to make an AND logic at the entry
of control unit between all of incoming signals.
2.3.3 Example of product between matrix and vector (MVP)
As an easy example we will implement MVP. This example shows us use of FDFG and FNG. Product of matrix and vector can be written in factorized way like this:
![]()
where:
From upper equation we can get the graph corresponding to the algorithm
specification of the factorized MVP ( see Figure 2.16)
Figure 2.16: FDFG of Matrix and Vector Product
In this example we will use matrix A which is 3 by 4 and vector B which is size 4. So we have m=3, n=4.
The interface with environment is presented on Figure
2.16 by infinite frontiers inside M,V,O and DOTP frontier. Inputs from
environment to application are realized by Fa infinite, Fb infinite and
Const infinite and output to environment is realized by J infinite. The
square brackets []i=1m correspond
to the frontier DOTP, which is repeated m=3 times. This frontiers selects
m lines of matrix A with Fa and only diffuses vector B with Fb to the inner
frontier. It also collects the result of inner frontier ACC at J. Function
of sum in equation corresponds to the inner most frontier ACC. This frontier
selects from the matrix A one line and it computes the result of equation
with I. Top frontier is only a construct, which holds whole application.
It can also serve as a testbench for hardware implementation of MVP.
On the Figure 2.17 you can see the relations
of control units of frontiers. This is frontier neighbourhood graph.
Figure 2.17: FNG of Matrix and Vector Product 1
This graph is rather unreadable, so we can make some adjustment and then we get a FNG graph as seen on Figure 2.18.
Figure 2.18: FNG of Matrix and Vector Product 2