Chapitre 5 : Formules de Taylor et développements limités
Exercice "VRAI ou FAUX"Le reste de Lagrange est o((b-a)n)
Vrai Faux
Exercice "VRAI ou FAUX"Les formules de Taylor sont dans un contexte général, alors que celles de Mac-Laurin sont pour a=0 et b=x
Vrai Faux
Sélection multiple
Soit f(x)=1+x-5x² +o(x3) au voisinage de 0
La partie principale de f est 1
| |
La partie principale de f est x
| |
La partie principale de f est 1+x-5x²
| |
Il s'agit d'un DL d'ordre 1
| |
Il s'agit d'un DL d'ordre 3
| |
Sélection multiple
Soit f une fonction definie sur un voisinage pointé d'un réel quelconque x0 et n un entier naturel quelconque, alors on a :
Si f admet un DL d'ordre n en x0, alors
Si f admet un DL d'ordre n en x0, alors
f admet un DL d'ordre p en x0 avec p>n
| |
f admet un DL d'ordre p en x0 avec p<n
| |
f n'admet pas de DL d'ordre p en x0 avec p | |
Sélection multiple
Le DL d'ordre 3 en 0 de sin(x²) est ...?
x² + o(x²)
| |
x² + o(x3)
| |
1 - x²/2 + o(x²)
| |
1 - x²/2 + o(x3)
| |
1 + x²/2 + o(x²)
| |
Exercice "VRAI ou FAUX"le DL d'ordre 3 de cos(1/(3x)) en +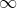
est
 "1-\frac{1}{18x^{2}}+o(\frac{1}{x^{3}})")
Vrai Faux
Exercice "VRAI ou FAUX"Le DL d'ordre 2 en 0 de ex-x vaut 1+x+x2/2+o(x2)
Vrai Faux
Exercice "VRAI ou FAUX"Le DL d'ordre 3 en 0 de xex vaut x( 1 + x + x²/2 + x3/3! + o(x3) ) = x + x² + x3/2 +x4/3! + o(x4)
Vrai Faux
Exercice "VRAI ou FAUX"Pour toute fonction f, dérivable sur un voisinage de 0 et admettant un DL d'ordre n en 0 de partie régulière A,
on a :
f' admet un DL d'ordre n en 0 de partie régulière A'
Vrai Faux
Exercice "VRAI ou FAUX"Pour toute fonction f, continue sur un voisinage de 0 et admettant un DL d'ordre n en 0 de partie régulière A,
on a :
la primitive de f admet un DL d'ordre (n+1) en 0 de partie régulière
dt "\int_{0}^{x}A(t)dt")
la primitive de f admet un DL d'ordre (n+1) en 0 de partie régulière
Vrai Faux