Chapitre 2 : Suites & Convergence

CHAPITRE 2 : Exercice "VRAI ou FAUX"


1.Notion de suite divergente

On a, pour toute suite réelle (Un) :


Vrai Faux


2. Notion de suite convergente

Soit une suite (Vn) qui a une fonction associée dont la représentation graphique est:

 


On a :

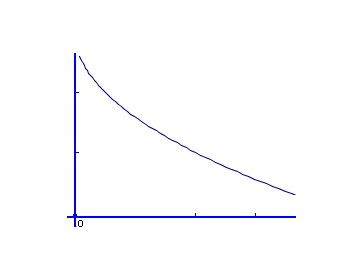
(Vn) converge vers 0

Vrai  
Faux 









3.Propriétés des suites convergentes
Soit (Un) une suite qui converge vers un réel : s
Toute suite extraite de (Un) est convergente, et tend vers s

Vrai  
Faux 









4.Propriétés des suites convergentes
Soit une suite (Un) convergente vers 2. 
Si on modifie  les 2010 premiers termes  de  la suite, alors (Un) convergera vers un autre réel.

Vrai  
Faux 









5.
On a :






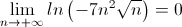
Vrai  
Faux 









6.Formes indéterminées 



On a :






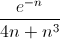
est une forme indéterminée.



Vrai  
Faux 









7. Croissances comparées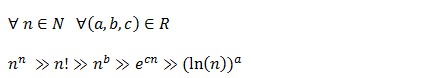 

Vrai  
Faux 









8.Compléments sur les opérations algébriques pour la détermination des limites 




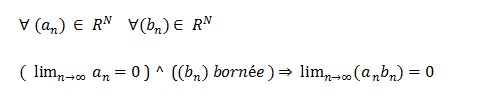
Vrai  
Faux 









9.Suites de Cauchy 



Pour toute suite réelle (un), on dit qu'elle est de Cauchy si, et seulement si :





Vrai  
Faux 









10.Suites de Cauchy
 
Pour toute suite (Un),
 (Un) suite de Cauchy 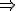    (Un) suite convergente 

Vrai  
Faux 









11.  Eléments sur la convergence des suites réccurentes


Pour toute suite réelle (Un) et pour toute fonction réelle R, on a :




Vrai  
Faux