- Programmer une classe VecteurEn2d pour représenter et manipuler les vecteurs dans l'espace euclidien de dimension 2.
a. Sur votre compte, créez un répertoire 'AlgèbreLinéaire'. Télécharger le fichier TP1.jar et enregistrez le dans le répertoire 'AlgèbreLinéaire'.
b. Sous BlueJ, ouvrez le fichier TP1.jar : Menu "Projet" -> "Open Project" et sélectionnez le fichier "TP1.jar".
c. Sous BlueJ, ouvrez les préférences (Menu "Tools" -> "Preferences..."), sélectionnez l'onglet "Miscellaneous" et cochez la case "Show unit testing tools".
Après avoir répondu à une question, cliquez sur le bouton "Run Tests" et vérifiez que l'indicateur de la question passe au vert. Si BlueJ indique une croix rouge pour la question que vous venez de résoudre cela veut dire que votre solution n'est pas correcte ! Si l'indicateur passe au vert cela veut dire que votre solution est peut-être correcte !
a. Créez dans votre projet une nouvelle classe VecteurEn2d (bouton 'New Class' sous Bluej). Inspectez son code ? Que contient-il ? Cela correspond-il à un vecteur en deux dimension ?
b. Ajoutez à la classe VecteurEn2d les attributs nécessaires pour que les objets de la classe VecteurEn2d représentent bien un vecteur de l'espace euclidien en dimension 2. Le type double sera utilisé pour représenter des nombres réels.
c. Ajoutez à la classe VecteurEn2d un constructeur à 2 paramètres de type double spécifiant la valeur du vecteur. La signature de ce constructeur est donc :
public VecteurEn2d(final double px, final double py)
d. Ajoutez à la classe VecteurEn2d deux accesseurs correspondant aux deux attributs, i.e., deux méthodes publiques retournant la valeur des attributs du VecteurEn2d courant et dont les signatures sont :
public double getX()
public double getY()
a. Sous blueJ, créez un Plan et un VecteurEn2d, puis invoquez la méthode dessinerVecteurEn2d de ce Plan en lui passant en paramètre l'instance du VecteurEn2d que vous venez de créer. Vérifiez que le dessin obtenu est bien conforme au vecteur que vous avez créé.
a. Ajoutez à la classe VecteurEn2d une méthode publique norme sans paramètre qui retourne la norme du VecteurEn2d courant.
Aide : Pour calculer la racine carrée d'un nombre réel (représenté par un double en Java) Java fournie la méthode sqrt de la classe Math. Par exemple, la ligne de code suivante a pour effet d'affecter à a la racine carré de b :
a = Math.sqrt(b);
b. Testez votre méthode sur quelques exemples en vérifiant qu'elle retourne bien une valeur conforme à la définition.
a. Ajoutez à la classe VecteurEn2d une procédure publique multiplicationScalaire à un paramètre qui multiplie l'instance courante du VecteurEn2d par le paramètre scalaire.
b. Testez votre procédure sur quelques exemples et vérifiez que son action est conforme à la définition.
a. Ajoutez à la classe VecteurEn2d une procédure publique sommeVectorielle à un paramètre qui somme le VecteurEn2d passé en paramètre à l'instance courante du VecteurEn2d.
b. Testez votre procédure sur quelques exemples et vérifiez que son action est conforme à la définition.
a. Ajoutez à la classe VecteurEn2d une fonction publique produitScalaire à un paramètre qui retourne le produit scalaire de l'instance courante du VecteurEn2d avec le VecteurEn2d passé en paramètre.
b. Tester votre méthode sur quelques exemples en vérifiant qu'elle retourne bien une valeur conforme à la définition.
a. Ajoutez à la classe VecteurEn2d une fonction publique estOrthogonal à un paramètre qui retourne une valeur booleene indiquant si l'instance courante du VecteurEn2d est orthogonale au VecteurEn2d passé en paramètre.
b. Testez votre méthode sur quelques exemples en vérifiant qu'elle retourne bien une valeur conforme à la définition. Testez en particulier le vecteur nul.
c. Ajoutez à la classe VecteurEn2d une fonction obtenirVectOrthogonal sans paramètre qui retourne un vecteur orthogonal à l'instance courante du VecteurEn2d.
d. Testez votre méthode sur quelques exemples en vérifiant qu'elle retourne bien une valeur conforme à la définition. Testez en particulier le vecteur nul.
e. Créez les vecteurs V et W de coordonnées (0.1 ; 9) et (-4.5 ; 0.05 ). Testez l'orthogonalité de ces vecteurs avec la méthode estOrthogonal.Le résultat obtenu est il conforme ? Multipliez V par 0.1 et re-testez l'orthogonalité. Le résultat est-il toujours conforme ? Pourquoi ?
a. Ajoutez à la classe VecteurEn2d une fonction publique estColineaire à un paramètre qui retourne un booléen indiquant si l'instance courante du VecteurEn2d est colinéaire au VecteurEn2d passé en paramètre.
b. Testez votre méthode sur quelques exemples en vérifiant qu'elle retourne bien une valeur conforme à la définition. Testez en particulier le vecteur nul.
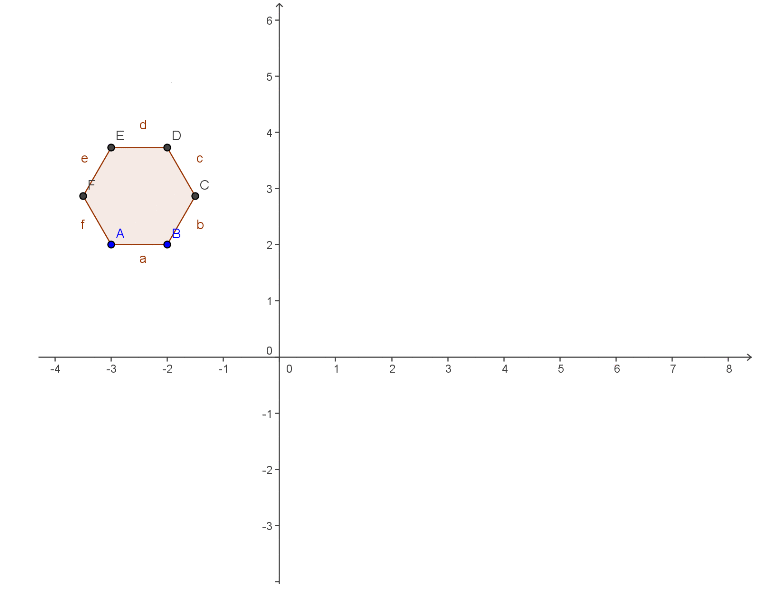
On a une tour de base hexagonale ABCDEF
A(-3 ; 2) B(-2 ; 2) C(-1,5 ; 2,87)

a. Trouvez les coordonnées des vecteurs de norme 1, u,v et w orthogonaux respectivement à AB, BC et CD.
b. On place un observateur en un point I, que voit-il lorsque I a les coordonnées suivantes : (0 ; -3), (0 ; 2), (-12.7/3.48 ; -0.87), (-1 ; 1) ? (on pourra calculer les produits scalaires u.IA , v.IB ….)
c. L’observateur doit se déplacer combien de fois pour se rendre compte que la base de la tour est un hexagone régulier ?
Soient 8 points du plans euclidiens définis par leurs coordonnées :
A : (-3 ; -2)
B : (-1 ; 2)
C : (1 ; 3)
D : (1 ; 0)
E : (-1 ; 1)
F : (4 ; 1)
G : (3 ; 4)
H : (0 ; 3).
a. A l'aide de vos programmes déterminez si ABCD , ABCE et DFGH sont des trapèzes, parallélogrammes ou carrés.
b. Dans les cas où les quadrilatères ci dessus sont des parallélogrammes, déterminez leur aire à l'aide de votre programme.
a. Ajoutez à la classe VecteurEn2d une fonction statique approche prenant trois paramètre de type double a, b et epsilon et retournant true si l'écart entre a et b est inférieur à epsilon.
b. Dans les méthodes de la classe VecteurEn2d, remplacez chaque test d'égalité entre deux variables de type double par un appel à la méthode approche avec une valeur d'epsilon suffisament petite (0,00001). Refaites les tests de la question 7e.
Sujet rédigé par Jean Cousty, Benjamin Perret et Leïla Reille pour l'unité A3PAL à ESIEE Paris.