A3PAL - Algèbre linéaire - TP5 : Coordonnées homogènes et projections
Objectif
- Ajouter à la classe Matrice programmée au TP précédent les méthodes permettant de construire les matrices de transformations géométriques usuelles (translation, homothétie, rotation) et les matrices de projections perspectives en coordonnées homogènes.
- Utiliser la classe Matrice pour obtenir une visualisation "fil de fer"
d'un cube se transformant en 3D, être capable de changer la position de l'observateur, comparer les différents types de projection.

L'objectif du TP est d'obtenir un rendu type "logiciel de conception assistée par ordinateur" (CAO) permettant de voir simultanément une scène 3D sous différents points de vue : projection orthognale vue de face (quart inférieur gauche), projection orthognale vue de dessus (quart supérieur gauche), projection orthognale vue de côté (quart supérieur droit) et vue perspective (quart inférieur droit).
Liste des compétences à acquérir pendant le TP:
- Représenter un vecteur en coordonnées homogènes ;
- normaliser la coordonnée homogène d'un vecteur ;
- déterminer les matrices de transformations géométriques (translation, rotation, homothétie) usuelles dans l'espace 3D homogène ;
- déterminer les matrices de projection orthogonal (suivant les axes du repère) de l'espace 3D homogène vers l'espace 2D homogène ;
- déterminer les matrices de projection perspective (suivant les axes du repère) de l'espace 3D homogène vers l'espace 2D homogène ;
- concevoir un logiciel de visualisation de type "CAO" en utilisant des transformations géométriques et des projections de l'espace 3D homogène.
0 - Travail préliminaire
a. Terminez le TP2 (au moins jusqu'à l'exercice 7 inclus).
b. Terminez le TP3 (au moins jusqu'à l'exercice 3 inclus).
b. Terminez le TP4 (au moins jusqu'à l'exercice 2.f inclus).
c. Créez une copie du répertoire correspondant au TP4 et renommez cette copie TP5. Sous blueJ, ouvrez le projet intitulé TP5 correspondant à la copie du TP4 que vous venez de créer.
1 - Coordonnées homogènes
Lors du passage en coordonnées homogènes, un vecteur v en dimension n: v=(v1 , ..., vn ) devient le vecteur v' en dimension n+1: : v'=(v1 , ..., vn , 1 ). De manière similaire, à un vecteur en coordonnées homogènes t' en dimension n+1 : t'=( t'1 , ..., t'n , w ) correspond le vecteur t en dimension n: t=( t'1 / w , ..., t'n / w ). Comme les classes Matrice et Vecteur codées dans les TPs précédents peuvent représenter des vecteurs et des matrices en dimension arbitraire, elles peuvent être utilisées pour représenter des vecteurs en coordonnées homogènes. Nous allons simplement ajouter des méthodes utiles à la manipulation de vecteurs en coordonnées homogènes.
a. Ajoutez à la classe Vecteur une procédure
publique normaliseHomogene sans paramètre qui normalise la coordonnée homogène du vecteur courant. Pour normaliser le vecteur en coordonnées homogènes v=( v1 , ..., vn , w ), il faut le multiplier par le scalaire 1/w, on obtient donc le vecteur v'=( v'1 , ..., v'n , 1 ).
b. Testez la procédure normaliseHomogene sur le vecteur ( 1, 2, 3, 4 ), vérifiez que le résultat est correct.
c. Ajoutez à la classe Matrice une procédure publique setHomothetieHomogene3d à un paramètre k de type double qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à l'homothétie de rapport k dans l'espace 3d homogène (c'est donc une matrice 4x4).
d. Testez la procédure setHomothetieHomogene3d en construisant la matrice d'homothétie de rapport 2, vérifiez que vous obtenez la bonne matrice. Appliquez la matrice d'homothétie au vecteur ( 1, 2, 3, 1 ) et vérifiez que le résultat est correct.
e. Ajoutez à la classe Matrice une procédure publique setTranslationHomogene3d à un paramètre t de type Vecteur qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à la translation de vecteur t dans l'espace 3d homogène (c'est donc une matrice 4x4, on suppose que t est un vecteur en dimension 3).
f. Testez la procédure setTranslationHomogene3d en construisant la matrice de translation de vecteur ( -1, -1, -1 ), vérifiez que vous obtenez la bonne matrice. Appliquez la matrice de translation au vecteur ( 1, 2, 3, 1 ) et vérifiez que le résultat est correct.
g. Ajoutez à la classe Matrice une procédure publique setRotationOxHomogene3d à un paramètre alpha de type double qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à la rotation d'angle alpha radian autour du vecteur ( 1, 0, 0 )dans l'espace 3d homogène (c'est donc une matrice 4x4).
h. Testez la procédure setRotationOxHomogene3d en construisant la matrice de rotation d'angle π/3, vérifiez que vous obtenez la bonne matrice. Appliquez la matrice de rotation au vecteur ( 1, 1, 1, 1 ) et vérifiez que le résultat est correct.
i. Ajoutez à la classe Matrice une procédure publique setRotationOyHomogene3d à un paramètre alpha de type double qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à la rotation d'angle alpha radian autour du vecteur ( 0, 1, 0 )dans l'espace 3d homogène (c'est donc une matrice 4x4).
j. Testez la procédure setRotationOyHomogene3d en construisant la matrice de rotation d'angle π/3, vérifiez que vous obtenez la bonne matrice. Appliquez la matrice de rotation au vecteur ( 1, 1, 1, 1 ) et vérifiez que le résultat est correct.
k. Ajoutez à la classe Matrice une procédure publique setRotationOzHomogene3d à un paramètre alpha de type double qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à la rotation d'angle alpha radian autour du vecteur (0,0,1)dans l'espace 3d homogène (c'est donc une matrice 4x4).
l. Testez la procédure setRotationOzHomogene3d en construisant la matrice de rotation d'angle π/3, vérifiez que vous obtenez la bonne matrice. Appliquez la matrice de rotation au vecteur ( 1, 1, 1, 1 ) et vérifiez que le résultat est correct.
2 - Projection othogonale
Une projection est une transformation qui réduit la dimension de l'espace.
Cela correspond à ce que l'on veut faire lorsque l'on dispose d'un objet en 3d (par exemple les coordonnées de points ou vecteurs)
que l'on veut visualiser sur un écran (donc en 2d).
Il existe plusieurs types de projection adaptés à ce problème et nous en étudions 2 : projections orthogonale et perspectives.
Projeter un point x de l'espace 3d orthogonalement sur un plan (2d) nécessite de considérer la droite orthogonale au plan et qui passe par le point x.
Cette droite intersecte le plan en un point y qui est le projeté de x sur le plan.
Comme y est dans un plan, on peut le repérer dans ce plan à l'aide de seulement 2 coordonnées, c'est à dire en 2d.
Par exemple si l'on projette orthogonalement x=(3, 5, 7) sur le plan OxOy, on obtient y=(3,5)
et si l'on projette sur OxOz on obtient y=(3,7).
Ces projections sont des applications linéaires et peuvent donc être représentées par des matrice et manipulées avec du calcul matriciel.
On s'intéresse ici à définir les matrices de projections orthogonales de l'espace 3d homogène dans l'espace 2d homogène. Les matrices à définir seront donc toutes de taille 3x4.
Rappel de cours: "Une projection est orthogonale lorsque la direction de projection est orthogonale au plan de projection et est un des axes du repère. Elle est utilisée en dessin technique pour obtenir les vues de face, de dessus et de coté. On obtient les coordonnées de l'image d'un point M en supprimant la coordonnée de la direction de projection."
a. Ajoutez à la classe Matrice une procédure publique setProjectionOrthoOxyHomogene3d sans paramètre qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à la projection orthogonale de l'espace 3d homogène dans l'espace 2d homogène correspondant au plan défini par les vecteurs ( 1, 0, 0 ) et ( 0, 1, 0 ) (la direction de projection est donc donnée par le vecteur ( 0, 0, 1 ) et la matrice est de taille 3x4).
b. Testez la procédure setProjectionOrthoOxyHomogene3d, vérifiez que vous obtenez la bonne matrice. Appliquez la matrice de projection au vecteur ( 1, 2, 3, 1 ) et vérifiez que le résultat est correct.
c. Ajoutez à la classe Matrice une procédure publique setProjectionOrthoOxzHomogene3d sans paramètre qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à la projection orthogonale de l'espace 3d homogène dans l'espace 2d homogène correspondant au plan défini par les vecteurs ( 1, 0, 0 ) et ( 0, 0, 1 ) (la direction de projection est donc donnée par le vecteur ( 0, 1, 0 ) et la matrice est de taille 3x4).
d. Testez la procédure setProjectionOrthoOxzHomogene3d, vérifiez que vous obtenez la bonne matrice. Appliquez la matrice de projection au vecteur ( 1, 2, 3, 1 ) et vérifiez que le résultat est correct.
e. Ajoutez à la classe Matrice une procédure publique setProjectionOrthoOyzHomogene3d sans paramètre qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à la projection orthogonale de l'espace 3d homogène dans l'espace 2d homogène correspondant au plan défini par les vecteurs ( 0, 0, 1 ) et ( 0, 1, 0 ) (la direction de projection est donc donnée par le vecteur ( 1, 0, 0 ) et la matrice est de taille 3x4).
f. Testez la procédure setProjectionOrthoOyzHomogene3d, vérifiez que vous obtenez la bonne matrice. Appliquez la matrice de projection au vecteur ( 1, 2, 3, 1 ) et vérifiez que le résultat est correct.
3 - Projection perspective
On s'intéresse ici à définir une matrice de projection perspectives de l'espace 3d homogène sur un plan homogène parallèle au plan Oxy situé à une distance d de l'origine dans la direction ( 0, 0, 1 ). La matrice recherchée est donc de taille 3x4.
Rappels : lorsque l'on cherche la projection perspective du point p=( px , py , pz ) sur le plan parallèle au plan Oxy situé à une distance d de l'origine dans la direction ( 0, 0, 1 ), la situation est schématisée dans la figure suivante (la dimension selon l'axe y n'est pas représentée pour simplifier mais les observations obtenus selon l'axe x se généralise directement à cette autre dimension):
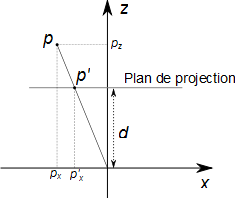
On cherche à déterminer les coordonnées ( p'x , p'y ) du point p' dans le plan de projection. Le théorème de Thalès nous donne immédiatement que pz / d = px / p'x, on en déduit: p'x = d*px / pz. De la même manière, on peut obtenir p'y = d*py / pz. Ce qui nous donne la matrice de projection suivante :
| 1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
0 |
1/d |
0 |
L'application de cette matrice de projection au vecteur en coordonnées homogènes 3d p=( px , py , pz , 1 ) nous donne le vecteur en coordonnées homogènes 2d ( px , py , pz/d ). La coordonnée homogène du résultat n'est alors pas normalisée. La projection complète s'obtient donc en appliquant d'abord la matrice de projection puis en normalisant le vecteur obtenu, ce qui donne au final le vecteur attendu : ( d*px / pz , d*py / pz ,1 ).
a. Ajoutez à la classe Matrice une procédure publique setProjectionPerspectiveOxyHomogene3d avec un paramètre de type double qui modifie l'instance courante de la classe Matrice afin qu'elle corresponde à la matrice de projection perspective définie ci-dessus.
b. Testez la procédure setProjectionPerspectiveOxyHomogene3d avec le paramètre 5.0, vérifiez que vous obtenez la bonne matrice. Appliquez la matrice de projection au vecteur ( 1, 2, 10, 1 ) et vérifiez que le résultat est correct.
4 - Application à la visualisation
L'objectif de ces questions est de produire une visualisation "technique", similaire à celle des logiciels de CAO (Conception Assistée par Ordinateur), où un objet 3d est vu simultanément de face, de côté et du dessus.
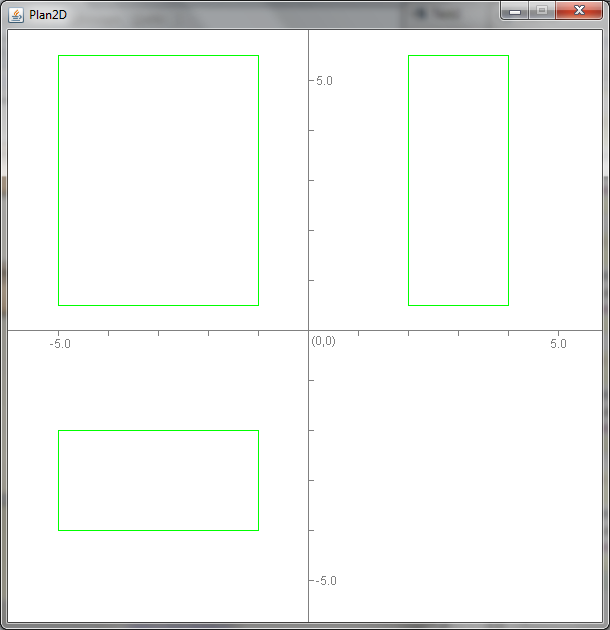 L'objectif est d'obtenir une visualisation similaire à celle d'un logiciel de CAO. Ici un même objet (un parallélépipède rectangle) est vue de face (quart inférieur gauche), de dessus (quart supérieur gauche) et de côté (quart supérieur droit).
L'objectif est d'obtenir une visualisation similaire à celle d'un logiciel de CAO. Ici un même objet (un parallélépipède rectangle) est vue de face (quart inférieur gauche), de dessus (quart supérieur gauche) et de côté (quart supérieur droit).
a. Téléchargez le fichier 'Test2.java' et importez la classe Test2 dans votre projet (sous Bluej, cliquer sur l'option 'add Class from File' à partir du menu 'Edit' et choissez le fichier 'Test2.java'). Cette classe, similaire à la classe 'TestCube' du TP précédent contient un squelette permettant de créer et afficher un parallélépidpède rectangle.
b. Dans la classe Test2, compléter la méthode getTransformee. Cette méthode prend en paramètre un tableau de vecteurs pVecteurs et une matrice pTransformation. Elle doit retouner un nouveau tableau de vecteurs contenant les images des éléments du tableau pVecteurs par la transformation pTransformation.
c. Dans la procédure test, avant l'invocation de la procédure qui dessine le parallélépipède à l'écran, créez une matrice de projection orthogonale sur le plan Oxy, appliquez la aux sommets du parallélépipède au moyen de la méthode getTransformee et affichez le résultat à l'écran. L'affichage est-il conforme à vos prédictions ? Que remarquez vous par rapport à l'affichage obtenu sans appliquer la matrice de projection ? Expliquez.
d. Quelle translation faut-il appliquer au parallélépipède si l'on souhaite qu'il apparaisse dans le coin inférieur gauche du repère ? Dans la procédure test, ajoutez maintenant une matrice de translation de manière à ce que le parallélépipède apparaisse dans le coin inférieur gauche du repère.
e. Dans la procédure test, créez une deuxième matrice de projection orthogonale sur le plan Oxz, appliquez la aux sommets du parallélépipède au moyen de la méthode getTransformee et affichez le résultat à l'écran. A quoi correspond ce que vous voyez ?
f. Quelle translation faut-il appliquer au parallélépipède si l'on souhaite que la projection obtenue à la question e. apparaisse dans le coin supérieur gauche du repère ? Dans la procédure test, ajoutez maintenant une deuxième matrice de translation de manière à ce que le parallélépipède projeté sur le plan Oxz apparaisse dans le coin supérieur gauche du repère.
g. Dans la procédure test, créez une troisième matrice de projection orthogonale sur le plan Oyz, appliquez la aux sommets du parallélépipède au moyen de la méthode getTransformee et affichez le résultat à l'écran. A quoi correspond ce que vous voyez ?
h. Quelle translation faut-il appliquer au parallélépipède si l'on souhaite que la projection obtenue à la question g. apparaisse dans le coin supérieur droit du repère ? Dans la procédure test, ajoutez maintenant une troisième matrice de translation de manière à ce que le parallélépipède projeté sur le plan Oyz apparaisse dans le coin supérieur gauche du repère.
L'objectif des questions suivantes est d'ajouter la vue perspective à la méthode test de la classe Test2:
i. Dans la procédure test, ajoutez une matrice de projection perspective sur le plan parallèle au plan Oxy et situé à une distance 8 de l'origine. Appliquez cette projection aux sommets du parallélépipède au moyen de la méthode getTransformee, normalisez le résultat et affichez le. Donnez une explication à ce que vous voyez.
j. Dans la procédure test, ajoutez une matrice de translation selon le vecteur (0,0,12). Appliquez cette transformation aux sommets parallélépipède avant d'effectuer la projection perspective. Vérifiez que le résultat est maintenant correcte.
k. Modifiez la translation introduite à la question j. de manière à placer le parallélépipèdedans le quart inférieur droit du repère. Vérifiez que le résultat est correcte.
l. Comment peut-on faire pour voir le parallélépipède sous un autre angle ? Testez votre solution.
Sujet rédigé par Jean Cousty, Benjamin Perret et
Leïla Reille pour l'unité A3PAL à ESIEE Paris.


