
Crédit photo : http://www.cuatrocuatros.com/
Une autre illustration artistique des principes mis en oeuvre dans ce TP.

- L'objectif de ce tp est d'utiliser les méthodes de visualisation 3D (projections, transformations) afin de créer une application permettant de "crypter" un texte en 3D. L'idée générale est de modifier intelligemment les coordonnées des points d'un objet 3D représentant ce texte de manière à ce que son aspect original n'apparaisse que si on le regarde depuis la bonne position. Le jeux consiste alors à retrouver la bonne position afin de lire le texte original.


L'idée générale est de partir de la constatation suivante : lors d'une projection perspective, une infinité de points est projetée sur le même point. Par exemple, dans la figure ci-dessous, p1 et p2 sont tous les deux projetés en p'. En fait tous les points de la droite définie par les points O (origine du repère) et p1 seront projetés sur p'. On appelle une telle droite, une ligne de perspective.
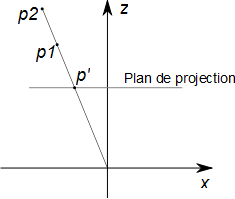
A partir d'un objet 3D, et d'une projection donnée, on peut donc bouger librement chacun des points de l'objet le long de ces lignes de perspectives et toujours obtenir le même résultat après projection. Par contre si l'on observe l'objet après déplacement de ses points le long des lignes de perspectives selon un autre point de vue, l'objet apparaîtra complètement déformé.
Commencez par télécharger le package BlueJ Crypto3D, ouvrez le et importez y vos fichiers Vecteur.java et Matrice.java obtenus au TP5.
Le but de cette section est de compléter la procédure deplacementObservateur de la classe CryptoText3D qui doit réaliser un déplacement de l'observateur dans la scène 3D. Cette procédure est appelée automatiquement dès que l'utilisateur déplace la souris dans la scène et reçoit en paramètre la nouvelle position de l'observateur. La particularité est qu'elle ne reçoit pas les coordonnées de l'observateur sous la forme de coordonnées xy dans le plan de l'écran mais sous forme de coordonnées sphériques: c'est-à-dire d'une longitude et d'une latitude.
L'idée centrale est ici de considérer que l'objet est toujours placé à l'origine. L'observateur, quant à lui, se déplace sur une demi-sphère dont le rayon est donné par l'attribut distanceCamera. Les coordonnées de l'observateur sur cette demi-sphère sont fonctions de la position de la souris sur l'écran. Finalement l'observateur regarde toujours vers l'origine, c'est-à-dire vers l'objet d'intérêt.
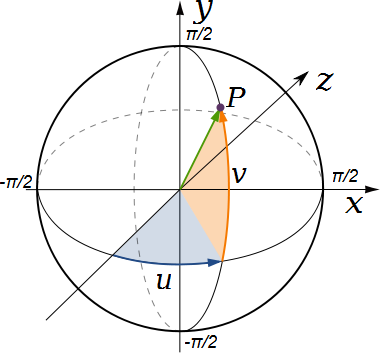 Figure adpatée de Wikipedia
Figure adpatée de Wikipedia
Les coordonnées reçues dans les paramètres u et v de la procédure mouseMove correspondent donc à la position (longitude, latitude) de l'observateur sur la demi-sphère.
Pour le moment, la procédure deplacementObservateur se contente d'appliquer une transformation perspective sur le texte et vous ne voyez rien car l'observateur et l'objet 3d se trouve au même endroit (à l'origine). Vous allez devoir créer et appliquer les transformations qui permettent de placer l'observateur à la bonne position.
a. Commencez par créer une translation qui va positionner l'observateur à la potision (0, 0, distanceCamera) et combinez la avec la transformation perspective déjà appliquée au texte .
b. Exécutez le programme et vérifiez que le texte s'affiche correctement.
c. Créez et appliquez une rotation qui va permettre de rendre compte de la latitude de l'observateur. Autour de quel axe faut-il effectuer la rotation ? Faut-il effectuer cette rotation avant ou après la translation ?
d. Exécutez le programme et vérifiez qu'en déplaçant la souris vers la haut ou le bas de l'écran, la vue change correctement. Pour vous aider dans votre interprétation du résultat, le point bleu sur la demi-sphère en haut à gauche de l'écran représente la position de l'observateur et vous devez considérer que le texte est au centre de la sphère.
e. Créez et appliquez une rotation qui va permettre de rendre compte de la longitude de l'observateur. Autour de quel axe faut-il effectuer la rotation ? Quand faut-il effectuer cette rotation ?
d. Exécutez le programme et vérifiez qu'en déplaçant la souris vers la gauche ou la droite de l'écran, la vue change correctement. Que se passe-t-il lorsque vous déplacer la souris de gauche à droite lorsque-vous êtes tout en haut (ou bas) de l'écran ? Expliquez.
Il est maintenant temps d'altérer l'objet 3D représentant notre texte de manière à ce qu'il ne soit lisible qu'à partir d'un point de vue particulier de notre demi-sphère. Nous souhaitons que, avec la bonne position de l'observateur, c'est-à-dire lorsque l'observateur est face au texte (latitude et longitude à zéro), le texte apparaisse normalement mais que dans toutes autres positions il soit méconnaissable. Le principe est le suivant:
Aide La classe Random fournit des objets capables de générer des nombres (pseudo) aléatoires. Ici vous allez devoir utiliser la fonction nextDouble de Random qui renvoie un nombre double sur l'intervalle [0,1] selon une répartition uniforme. La classe CryptoTexte3D dispose d'un attribut de type Random appelé rnd. Random sur la Javadoc
a. Écrivez la fonction deplacementAleatoire qui a pour but de déplacer aléatoirement un vecteur sur sa ligne de perspective. Elle reçoit en paramètre un vecteur pv. Les différentes étapes à réaliser dans cette fonction sont:
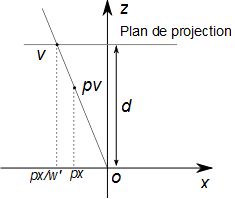
b. Écrivez la fonction cryptage qui a pour but de réaliser le cryptage complet d'un objet 3D. Cette fonction prend en paramètre un objet 3D sous la forme d'un tableau de Vecteur et renvoie un objet 3D crypté. Les différentes étapes à réaliser dans cette fonction sont:
c.Exécutez votre programme et vérifiez le résultat. Le texte devrait apparaitre normalement lorsque la souris se trouve au milieu de la fenêtre et brouillé partout ailleurs.
d.Maintenant le seul problème restant est que le texte décrypté apparait toujours pour la même position d'observation (latitude et longitude à zéro). Pour résoudre ce problème et rendre ainsi le jeux plus intéressant, on va modifier aléatoirement l'orientation du texte dans le constructeur (avant ou après le cryptage ?). Dans le constructeur de la classe CryptoText3D, déclarez et initialisez aléatoirement 2 variables locales r1 et r2 de type double avec des valeurs comprises entre -pi/2 et pi/2 (utilisez l'objet rnd) puis appliquez une rotation d'angle r1 autour de l'axe oY suivi d'une rotation d'angle r2 autour de l'axe oX.
e. Exécutez votre programme et vérifiez le résultat. La bonne position pour voir le texte en clair devrait maintenant être placée aléatoirement sur la fenêtre.
Sujet rédigé par Jean Cousty, Benjamin Perret et Leïla Reille pour l'unité A3PAL à ESIEE Paris.