Ce travail présente une méthodologie, basée sur l'apprentissage stochastique, destinée à la construction d'une architecture permettant la détection des défauts et le diagnostic dans le cas du mélangeur réacteur en continu (''Continuous Stirred Tank Reactor'' - CSTR). Notre approche est basée sur l'utilisation des Modèles de Markov Cachés (ou ''Hidden Markov Models'', HMM). En utilisant des procédures d'apprentissage hors ligne, on peut construire différents modèles de défauts en se basant uniquement sur les données mesurées. Le diagnostic en ligne peut ainsi être réalisé en utilisant ces modèles.

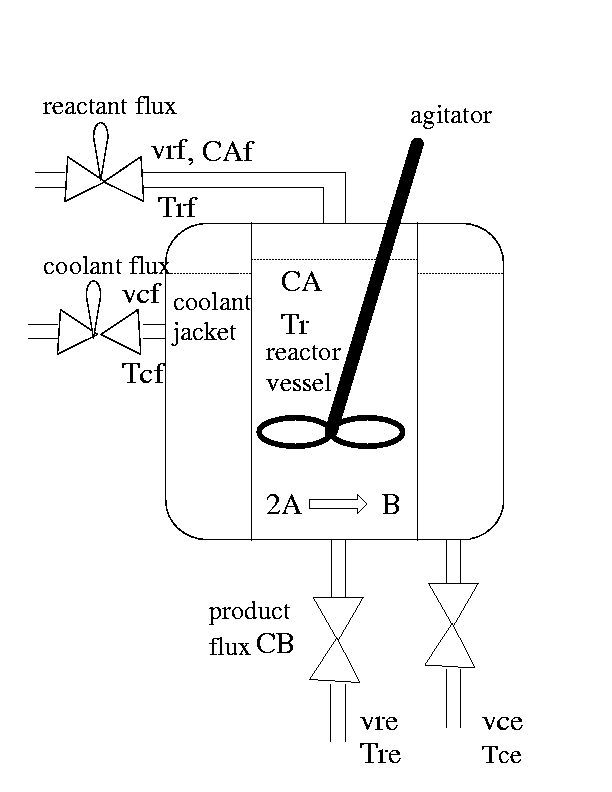
Nous présentons ici l'application de cette méthode au CSTR schématisé dans la figure ci-dessous. Les éléments composants un CSTR sont : la cuve de réaction, la cuve de contention, les tuyaux d'entrées et de sorties des composants de base, du réfrigérant et des produits finaux, les vannes, le système mélangeur et l'échangeur de chaleur.

Un réacteur chimique est un réservoir dans lequel se produit une réaction nécessitant plusieurs composants de base pour obtenir un certain produit. Le réacteur sera considéré comme opérant en continu. Un flux continu de composants de base est introduit dans la cuve et un flot continu de produit la quitte. La réaction a lieu à l'intérieur du réacteur. Un système de mélangeur effectue le mélange entre composants de base et produits et une homogénéité satisfaisante des propriétés physico-chimiques de la mixture.

Dans ce travail cinq défauts sont simulés : défaut d'arrivée des constituants de base, défaut d'arrivée du réfrigérant, défaut de la vanne du réacteur, défaut de la vanne du réfrigérant et défaut sur le coefficient d'échange de l'échangeur thermique. Dans notre simulation, nous avons utilisé la boîte à outils HMM pour l'apprentissage la détection et la reconnaissance des défauts.

Pour la démonstration, deux séquences d'observations ont été créées, une correspondant à un fonctionnement nominal et l'autre à un fonctionnement défectueux.

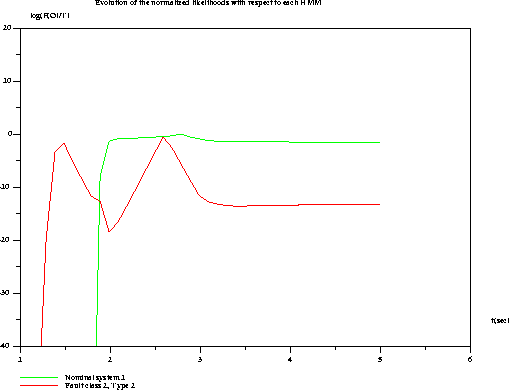
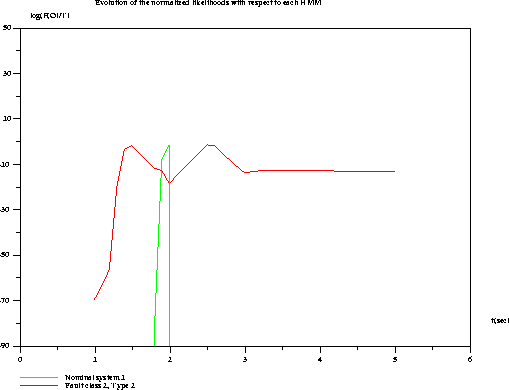
Les résultats obtenus sont satisfaisant comme on peut le constater sur les figures ci-dessous, qui représentent l'évolution de Log(p(O/l^w)) dans le temps. La même expérience a été faite en utilisant l'ensemble complet de HMM pour chacun des défauts. Les résultats ont été jugés satisfaisants pour toutes les séquences et la généralisation obtenue peut être considérée comme bonne.

(a)	(b)	(c)