The initial datas are really very noisy so before every attempt to identify the coefficients of the model, we need to filter it. The used filter is a numerical 8th orderlow pass Butterworth filter who cut all the frequency greater than 0.1Hz. This filter will be apply both on the input and output data. For efficiency reason the identification will be performed only with a reduced set of data. The identification window used by our programm is from order of 40 secondes (that means 200 points), but we can easly increase this duration for the studie of specific subject for example. This filtering is very efficient in term of noise reduction but in case of real time identification increase the delay between input and output of our system.
After several test the method used for the identification is a Recursive
Prediction Error Method (RPEM) inspired by the primitive function used in
Matri 
. We
choose a recursive method instead of batch method in order to use it eventually
in real time for a direct diagnosys help.
The underlaying model is a common ARMAX model:
Where y and u are the input and output of our system, 
represent the
noise, A, B and C are polynoms respectively of order na, nb and nc
and nd is the number of pure delay between the input and the output. This
Armax model can be rewritten as:
where 
is the vector of the coefficients of our model plus the
coefficients of the noise polynom C, so:
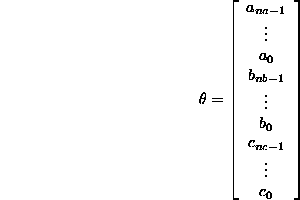
and 
is the vector of the last values from y u and so:
The last nc elements of are unknown therefore a recursive algorithm
which estimate 
is required. To insure a most fast convergency of
the algorithm we work with a moving set of ten points for both the input and
the output of the system using the previous coefficients at each steep of our
algorithm to initialize the new vector.