TD1 - SquareMatrix
Your native language: with Chrome, right-click on the page and select « Translate into … »
English version:
L’objectif de cette page est de développer une classe template matrice carrée (square matrix). Sa réalisation demande une bonne maîtrise de plusieurs notions abordées dans les fiches de cours précédentes. Nous allons procéder itérativement en implémentant les fonctionnalités par étapes successives.
Convention
Rappel
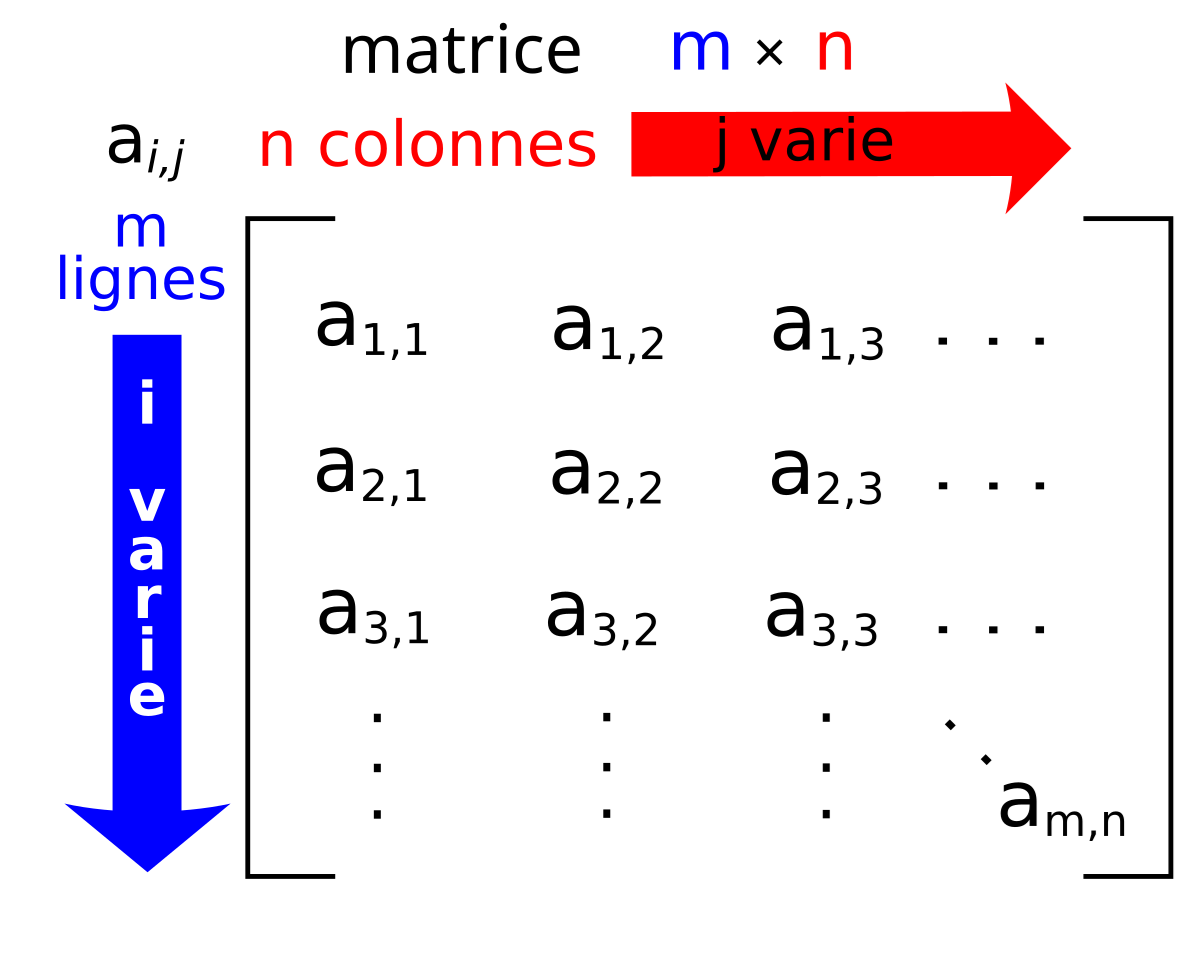
Notations :
Une matrice \(M_{mn}\) contient m lignes et n colonnes.
L’élément \(m_{ij}\) se trouve sur la ligne i colonne j.
La notion \(m_{ij}\) peut être contre-intuitive car en géométrie 2D, elle correspond à \(m_{yx}\) et non \(m_{xy}\)
L’addition de deux matrices de taille \(M_{mn}\) est une matrice de taille \(M_{mn}\)
La multiplication de deux matrices de taille \(M_{mn}\) et \(M_{np}\) est une matrice de taille \(M_{mp}\)
Constructeurs et affichage
Objectif
La taille de la matrice carrée est un paramètre du template. Les valeurs stockées dans les matrices seront de type int pour faciliter les tests unitaires.
Pour cette étape, vous devez mettre en place :
Un paramètre template indiquant la taille de la matrice
Un container de données de la STL
Un constructeur par défaut sans initialisation des valeurs
Un constructeur initialisant la matrice ligne par ligne à partir de valeurs entières passées en paramètre.
Une fonction d’affichage print()
Le met clef const à tous les endroits vous semblant judicieux
template ...
class SquareMatrix
{
private:
// internal data
...
public:
// default constructor
Matrix() {}
// constructor receiving a list of values
Matrix(array<...> & data) { ... }
// display
void print() { ... }
};
Remarque : l’écriture {1,2,3,4,5,6,7,8,9} est compatible avec l’initialisation d’un array (ou d’un vector), ainsi le constructeur paramétrique reçoit une const référence sur un std::array temporaire/anonyme.
Affichage
L’affichage produit par la fonction print est optimisé pour les nombres entiers entre 0 et 99. Le format d’affichage à respecter est le suivant :
Deux colonnes par valeur.
Une colonne d’espacement entre les valeurs.
Test
Vous devez mettre en place un code capable d’exécuter la fonction test1() ci-dessous. Vous devez obtenir un affichage identique.
using SM3 = SquareMatrix<N>;
void test1()
{
// initialization with values
SM3 M({ 11, 2, 3, 4, 55, 6, 7, 8, 99 });
M.print();
cout << "End of test 1------------" << endl;
}
>> 11 2 3
>> 4 55 6
>> 7 8 99
Opérateurs d’accès
Objectif
L’opérateur d’indexation [] n’accepte qu’un seul argument. Il n’est donc pas possible en C++ de mettre en place une syntaxe de la forme M[i,j].
Il est possible de chaîner deux opérateurs d’indexation en écrivant [i][j] mais cela suppose que l’on créé une classe intermédiaire pour retourner une ligne de la matrice ce qui complexifie l’exercice.
Pour l’instant, nous choisissons l’option la plus simple en surchargeant l’opérateur () et lui transmettant les deux indices i et j : (i,j). Nous vous demandons de respecter la convention suivante :
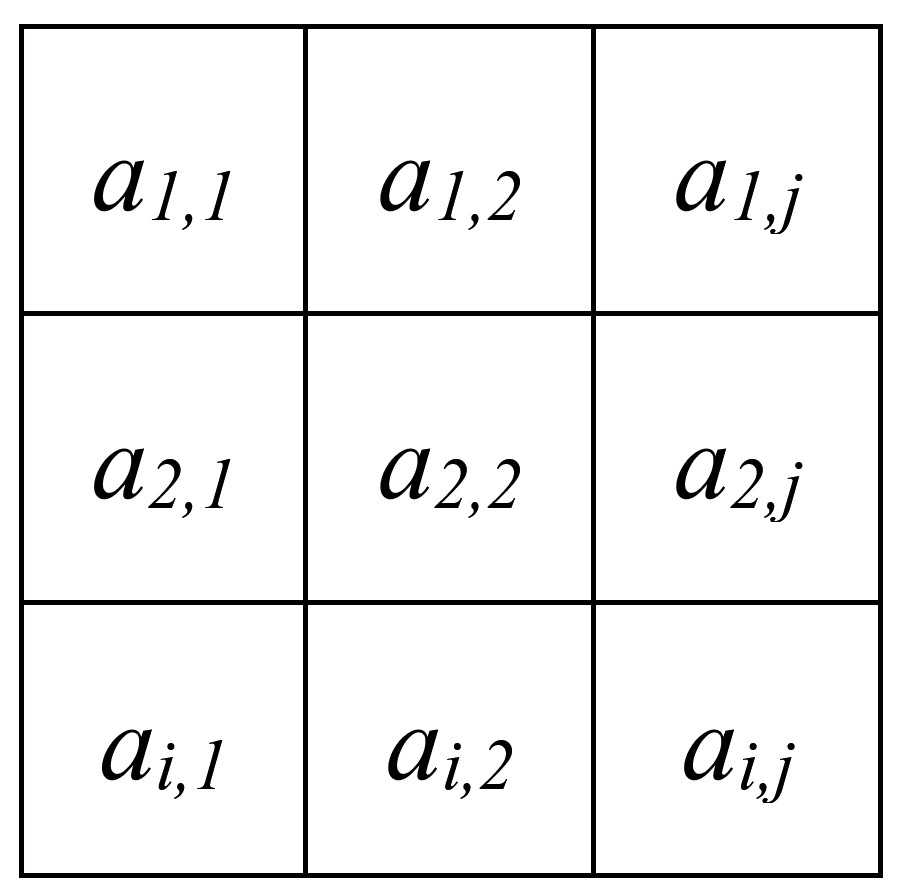
Fournissez une version const et non const de ce getter.
Test
Vous devez mettre en place une classe capable d’exécuter le code de test fourni ci-dessous :
const int N = 3;
using SM3 = SquareMatrix<N>;
void fnt2(const SM3 & M)
{
cout << M(0, 0);
}
void test2()
{
// example of usage
SM3 M;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
M(i, j) = i * i + j;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
if (M(i, j) != i * i + j)
cout << "ERROR";
fnt2(M);
cout << "End of test 2" << endl;
}
Initialiseurs supplémentaires
Ajoutez à la classe matrice les fonctions suivantes :
Une fonction membre diag() initialisant la matrice pour qu’elle corresponde à une matrice diagonale.
Une fonction membre fill(…) qui initialise les valeurs de la matrice à partir de la valeur fournie en argument.
Effectuez des affichages pour contrôler votre travail.
Transposition
Ajoutez :
Une fonction membre transpose() qui transpose les valeurs actuelles de la matrice (inplace).
Une fonction externe … t(…) qui retourne une nouvelle matrice correspondant à la transposée de la matrice passée en paramètre.
Écrivez un test pour valider votre implémentation.
Affichage
A partir de maintenant, toutes les fonctions ajoutées dans le code sont des fonctions externes à la classe (pas de fonction membre).
Surchargez l’opérateur << pour afficher le contenu de la matrice dans le même format que précédemment.
ostream& operator << (ostream& os, ... )
{
...
return os;
}
Lorsque l’on écrit : cout << M, l’objet cout est un objet global et unique correspondant à l’écran. Il faut donc le passer uniquement par référence pour éviter toute copie. Le paramètre de droite correspond à la matrice transmise lors de l’appel. L” opérateur << retourne l’objet cout afin de permettre le chaînage comme dans l’écriture suivante : cout << M1 << M2 << endl;.
Écrivez un test pour valider votre implémentation.
Opérateurs
Objectifs
Mettez en place les opérateurs externes suivant :
Addition et soustraction de deux matrices
Multiplication entre deux matrices
Multiplication d’une matrice par un entier (gauche et droite)
friend keyword
Comme nous créons des opérateurs externes (non membre de la classe), ils ne peuvent accéder aux données privées et doivent donc utiliser les accesseurs publics. Cependant, il est possible d’accéder aux données privées d’une classe depuis une fonction externe. Pour cela, il faut écrire la déclaration de cette fonction à l’intéreur de la classe et lui ajouter le qualificatif friend comme ceci :
template ...
class SquareMatrix
{
...
template ... friend ... operator+(...,...);
};
Clarifions la syntaxe de déclaration d’une fonction en C++, on doit mettre dans l’ordre :
Le template en premier, si nécessaire
Les qualificatifs - 0 1 ou plusieurs - inline/static/friend
Le type de retour
Le nom de la fonction + ses paramètres
Test final
Objectif
On doit pouvoir effectuer le calcul suivant avec votre classe :
Test
Vous devez pouvoir compiler et exécuter la ligne suivante :
A = A * t(A) + 2 * A - A * A;
Utilisez la matrice A= [ [1,2,3], [2,3,4], [3,4,5]] pour tester votre résultat. Vous devez obtenir :
>> 2 4 6
>> 4 6 8
>> 6 8 10
Travail à rendre sur Github Classroom
Tout le code doit contenir dans un seul fichier
Tous les tests demandés doivent être présents et actifs depuis le main()
Renommez votre fichier FINAL_SquareMatrix.cpp
Uploadez le fichier sur votre espace github
Ce projet est évalué et compte dans votre note finale.
Tout code généré automatiquement ou ne respectant pas les consignes rapporte 0 point.