TD2 - Object-oriented design

Your native language: with Chrome, right-click on the page and select « Translate into … »
English version:

Ce TD a pour objectif de vous faire concevoir le modèle objet le plus adapté pour répondre à une problématique technique. La quantité de code à produire n’est pas forcément importante, cependant il va falloir étudier en profondeur les différentes choix de modélisation pour trouver le plus adéquat. Il est tout à fait normal de tâtonner et d’essayer plusieurs options. Il est encore tout à fait normal que ces options s’avèrent infructueuses pour diverses raisons. La conception d’un modèle objet adapté à un besoin spécifique nécessite plusieurs essais. Nous vous proposons dans le cadre de ce TD d’effectuer cette exploration de manière guidée.

Par soucis de simplification, nous travaillons avec une classe matrice minimale :

Pas d’utilisation de template

Taille fixe (3x3 ou 2x2)

Utilisant des valeurs entières

Avec 1 constructeur sans arguments

Avec 1 constructeur avec une liste de valeurs

Un couple de Getter / Setter

Sans opérateurs arithmétiques

Les structures de données sous-jacentes sont laissées à votre libre choix.

Le contexte

Dans le domaine des réseaux de neurones profonds (deep-learning) ou des calculs appliquées (simulation physique, rendu 3D..), on utilise des matrices de très grande taille. La quantité de données est si importante (plusieurs Gigas) qu’il faut faire très attention pour arriver à stocker l’intégralité des données en mémoire vive. Dans ce contexte, on cherche à limiter la consommation de la mémoire pour ces deux opérations :

Copie d’une matrice

Construction de la transposée d’une matrice

Voici un code exemple :

matrice    M({ ...});
auto T   = M.transpose();
auto E   = T.copy();

Ces deux opérations, sans effort particulier, entraînent la duplication des données de la matrice M, triplant l’espace mémoire utilisé ! Nous devons donc mettre en place un système garantissant que ces deux opérations n’allouent pas de mémoire supplémentaire.

Un de vos camarades a utilisé la librairie Numpy de calcul matriciel. Il explique que cette librairie a mis en place une solution basée sur les vues : une vue correspond à une matrice ne contenant pas de données propres. Toutefois, elle présente la même interface, avec les mêmes accesseurs (getter/setter), de sorte que l’utilisateur ne perçoit aucune différence entre la vue et la matrice originale. Comme elle ne possède pas de données propres, la vue permet d’éviter la surconsommation de mémoire.

Cahier des charges

Voici la liste des demandes :

Chaque objet doit fournir des getter/setter

Depuis un objet M, on doit fournir deux méthodes permettant de retourner :

La transposée de M

Une copie de M

Les objets retournés par ces deux fonctions ne doivent pas dupliquer de données. L’optimisation de la mémoire reste la priorité absolue.

Avertissement

Nous vous présentons ci-dessous deux choix d’implémentation, probablement ceux auxquels vous penserez en premier. Nous tenons à les introduire, car ils conduisent à des écueils ; cela vous permettra de comprendre plus rapidement pourquoi. Trouver la bonne modélisation est très difficile et demande une véritable remise en question de l’énoncé de départ.

Proposition 1

Un de vos camarades fait une première proposition : la classe matrice étant déjà programmée, il suffit de créer la classe vue par dérivation de cette dernière et de lui ajouter un lien pointant vers les données de la matrice originale. Cette approche soulève un premier problème : la classe vue héritant de matrice, elle contient aussi un champ de données et même s’il n’est pas utilisé, il prend de la place en mémoire. Pour résoudre ce problème, votre camarade propose alors d’utiliser des vector plutôt que des array, l’avantage étant qu’en l’absence de données, l’objet vector vide prendra peu de place en mémoire.

Un autre camarade fait remarquer que l’on pourrait inverser le sens de l’héritage. Tout d’abord, on met en place une classe Vue sans champ de données et ensuite une classe Matrice héritant de Vue et augmentée d’un container de données quelconque.

Un dernier camarade conclut : si l’héritage n’a rien d’évident, alors faisons une unique classe VueMatrice qui peut prendre le rôle de l’une ou de l’autre classe en fonction d’un attribut interne.

Voici ci-dessous un résumé de ces trois propositions :

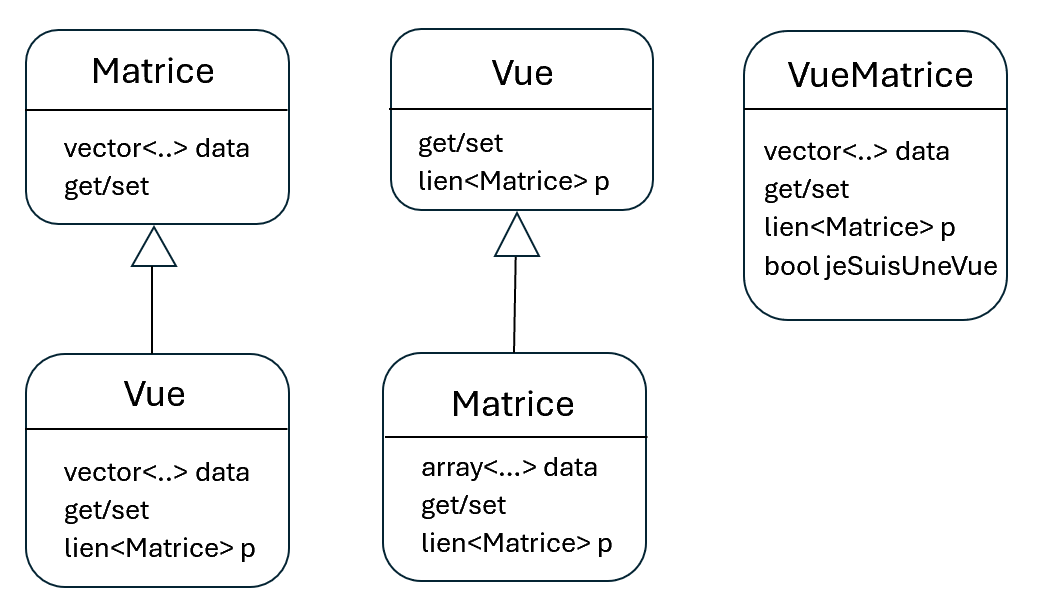
Voici un grand moment d’hésitation : qui doit hériter de qui et doit-on se passer de l’héritage ? Il est difficile de savoir et aucun argument ne semble plus convaincant qu’un autre :

Dans le premier scénario, la classe Vue contient un champ de données vide qu’on ne doit pas utiliser, c’est un peu bancal.

Dans le deuxième, la classe matrice fille contient un lien vers une autre matrice, lien qui ne doit pas être utilisé.

Le troisième scénario s’avère en fait similaires aux précédents, l’héritage a juste été masqué par l’utilisation d’un test:

If (ViewClass) {…} else {…}

Cas pratique

Nous considérons le code suivant :

vue test()
{
        Matrice    M({ ...});
        Vue V    = M.copy();
        return  V;
}

Quelle que soit l’option choisie pour modéliser la classe Matrice et la classe Vue, nous avons un problème majeur :

Lorsque l’on atteint la fin de la fonction test(), la matrice M est détruite car c’est un objet local. Le champ de données contenu dans M est donc aussi détruit dans la foulée. La vue V retournée par cette fonction est donc associée à un objet détruit. Le fait que V dispose d’un smart pointeur vers M, ne change rien au problème.

Nous nous permettons de vous donner un dernier indice : dans les modélisations proposées, un de nos problèmes est qu’il y a redondance :

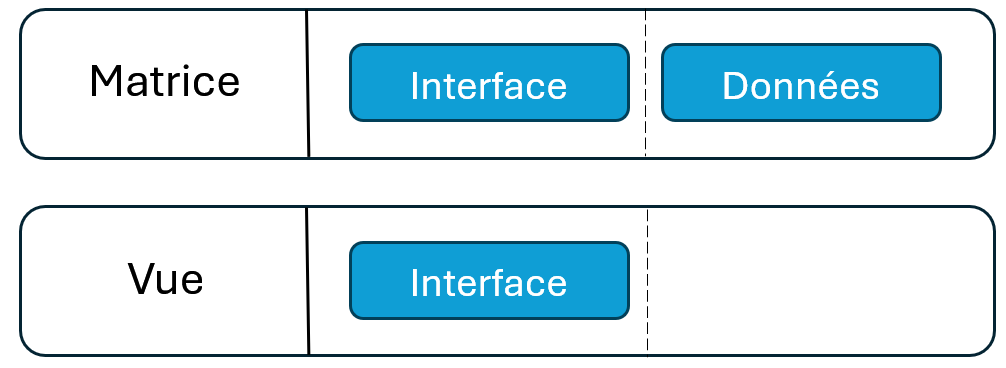
En effet, la classe Matrice :

Gère les données

Propose une interface de getter/setter

et la classe Vue :

Propose une interface de getter/setter

S’il est tout à faice concevable que la classe Matrice dispose des données et pas la classe Vue, il est plus étrange que ces deux classes proposent la même interface. En effet, cette redondance crée de la confusion alors qu’en POO, on cherche plutôt à ce que chaque classe tienne un rôle bien identifié.

Grâce à cette dernière remarque, essayez de trouver une modélisation répondant facilement à tous nos besoins.

Scénarios de tests

Vous êtes maintenant en chemin pour proposer un modèle objet fonctionnel. Pour être sur que vous avez fait le bon choix, voici plusieurs situations complexes que votre modèle doit pouvoir gérer.

Dissociation

On va s’intéresser ici au cas suivant :

Création d’une matrice M1

Création d’une copie M2 de M1

Si une valeur de M1 ou de M2 est modifiée, alors chaque objet devient indépendant. La modification ne porte que sur l’objet modifié, pas sur l’autre.

Matrix M1({1,2,3,4});
auto M2 = M1.copy();
M2(0,0) = 8;
cout << M1;
cout << M2;

>> 1,2
>> 3,4

>> 8,2
>> 3,4

On peut complexifier ce cas en considérant un objet M1 et deux de ses copies M2 et M3. La modification d’un de ces objets déclenche sa dissociation du groupe.

Matrix M1({1,2,3,4});
auto M2 = M1.copy();
auto M3 = M1.copy();
M2(0,0) = 8;
cout << M1;
cout << M2;
cout << M3;

>> 1,2
>> 3,4

>> 8,2
>> 3,4

>> 1,2
>> 3,4

En mémoire, il y a seulement 2 containers de données, un pour le groupe M1/M3 et l’autre pour M2.

Survie

Supposons que M2 soit une copie de M1 et que M1 soit détruite, M2 doit lui survivre et l’accès aux valeurs de M2 ne doit pas provoquer d’erreur.

Matrix test()
{
   Matrix M1({1,2,3,4});
   auto M2 = M1.copy();
   return M2;
}

int main()
{
   auto M3 = test();
   M3.print();
}

>> 1,2
>> 3,4

Cascadage

On pense ici au cas où l’on crée une copie M2 d’un objet M1 et une copie M3 depuis M2 et ainsi de suite… A la fin des ces opérations, les données doivent être représentées une seule fois en mémoire.

Matrix M1({1,2,3,4});
auto M2 = M1.copy();
auto M3 = M2.copy();
auto M4 = M3.copy();

Nous soulevons une question : comment organiser ces dépendances ? Lorsque nous cascadons plusieurs copies, au moment où l’on appelle la fonction get() de M10, va-t-elle appeler la fonction get de M9 qui à son tour va propager sa demande vers M8 et ainsi de suite ? Cet empilement d’appels engendrerait une perte de performance notable : 10 copies imbriquées impliqueraient 10 appels à la fonction get pour résoudre le get initial. Il faut éviter cette situation.

Etape 1 : mise en place

Codez votre modélisation avec une classe offrant :

Des accesseurs

La fonction copy()

Validez votre implémentation en testant les scénarios : dissociation, survie et cascadage

Etape 2 : transposée

Mise en place de la transposée

On peut remarquer que la transposée d’une transposée amène à la situation initiale. Ainsi, on peut gérer simplement ce cas en indiquant si la vue courante correspond à une transposition. Les accesseurs peuvent tenir compte de cette information pour accéder à la bonne cellule de la matrice.

Ajoutez la gestion de la transposée

Les cas connexes, comme la dissociation d’une transposée, doivent générer une matrice valide

Validez en ajoutant des scénarios de test

Etape 3 : en mode pro

Nous avons rempli les objectifs demandés, mais nous devons penser aux utilisateurs. En effet, même si notre modélisation fonctionne correctement, nous n’avons pas traité toutes les syntaxe possibles et si l’on tient à faire un travail professionnel, il faut que la classe Matrice propose suffisamment d’options pour couvrir toutes les syntaxes habituelles.

Constructeur de recopie

Voici sa syntaxe :

Syntaxe du constructeur de recopie :

Matrice(const Matrice& other)

Ce constructeur est appelé lorsque l’utilisateur écrit le code suivant :

Matrice S(M);
Matrice T = M;

Commentaire :

Ligne 1 : La première ligne est évidente puisqu’elle correspond à la syntaxe associée au constructeur de recopie : un objet de même type est transmis au constructeur pour créer un nouvel objet qui correspondra à une copie.

Ligne 2 : La deuxième ligne est moins évidente. En effet, en voyant un signe =, on aurait tendance à penser que c’est un opérateur d’affectation qui sera appelé. Cependant, il n’en est rien. Comme l’objet T n’existe pas encore et qu’il est créé à cette ligne, c’est bien une construction depuis un objet existant M qui s’opère, d’où l’appel au constructeur de recopie.

Travail à effectuer : Ajoutez un constructeur de recopie à votre classe Matrice et testez le.

Opérateur d’affectation

Prenons un exemple :

A = B;

Lorsque la ligne A=B est exécutée, il ne s’agit pas d’une construction puisque l’objet A existe déjà. Les ressources de A sont ainsi réutilisées pour recopier les données de B. Il y a donc appel de l’opérateur d’affectation pour gérer ce cas :

Syntaxe de l’opérateur d’affectation :

Matrice& operator=(const Matrice& other)

Travail à effectuer : Ajoutez un opérateur d’affectation à votre classe matrice et testez le.

Travail à rendre sur Github Classroom

Tout le code doit contenir dans un seul fichier

Tous les tests demandés doivent être présents et actifs depuis le main()

Renommez votre fichier FINAL_View.cpp

Uploadez le fichier sur votre espace github

Ce projet est évalué et compte dans votre note finale.

Tout code généré automatiquement ou ne respectant pas les consignes rapporte 0 point.