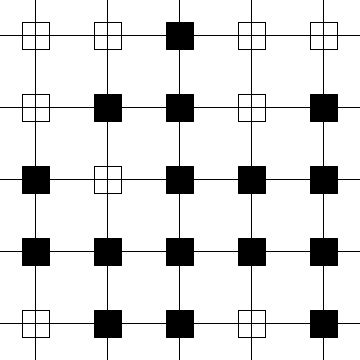Equipe SDI: recherche: ordres et topologie numerique

Ordres et topologie numérique

Personnes impliquées : Gilles Bertrand, Michel Couprie, Christophe Lohou.

Dans l'approche classique introduite par A. Rosenfeld et dénommée ``topologie numérique'' (digital topology), les éléments de Zⁿ sont liés par des relations d'adjacence (par exemple la 4- ou la 8-adjacence dans Z²). Ces relations correspondent à une structure de graphe, elles permettent de définir des notions de nature topologique comme les notions de connexité, de bord, de courbe simple. Cependant, il n'y a aucun moyen évident de construire une topologie au sens habituel du terme, à partir de ces notions.

Une approche différente a été introduite par E. Khalimsky sous le nom de ``connected ordered topological spaces (COTS)'', dans cette approche on considère un espace Hⁿ associé à Zⁿ , dans lequel le plus petit voisinage associé à un point de Hⁿ diffère d'un point à l'autre (Fig 1). Ceci permet de définir une topologie associée à Zⁿ. L'approche basée sur les complexes cellulaires, qui sont des ensembles d'éléments de différentes dimensions appelés cellules, permet également de définir une topologie. Dans ces deux derniers cas, la topologie obtenue est une topologie d'Alexandroff, c'est-à-dire une topologie telle que toute intersection (finie ou non) d'ouverts est un ouvert. On peut montrer que la donnée d'une topologie d'Alexandroff est équivalente à la donnée d'une structure d'ordre, c'est-à-dire d'une relation réflexive, transitive et antisymétrique.

Nous proposons dans le cadre des ordres un ``modèle'' des notions issues du cadre de la topologie numérique. A tout objet (sous-ensemble) de Zⁿ, nous associons un objet dans l'ordre Hⁿ (voir Fig. 1). Il est alors possible ``d'interpréter'' un objet de Zⁿ dans un espace qui possède de bien meilleures propriétés. Nous validons ce modèle en considérant les notions fondamentales de point simple et de surface [Ber99, BC99].


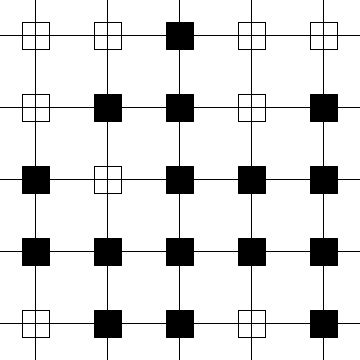(a)	(b)

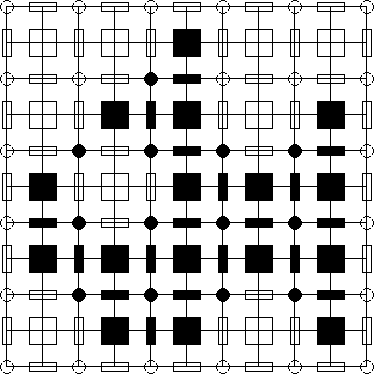
Figure 1: (a): Un sous-ensemble X de Z² (carr\'es noirs). (b): Un sous-ensemble de H² associ\'e \`a X.
Le voisinage d'un carré est constitué de lui-même et des huit éléments plus petits qui l'entourent ; le voisinage d'un rectangle est constitué de lui-même et des deux disques qui l'entourent ; le voisinage d'un disque se compose uniquement de ce disque.