Points simples et homotopie
Personnes impliquées : Gilles Bertrand, Michel Couprie,
Christophe Lohou.
Un point simple est un point d'un objet dont l'enlèvement ne
modifie pas la topologie de l'objet (voir Fig. 2).
Cette notion est à la base de tous les algorithmes
permettant d'analyser une image selon des critères
topologiques. Nous avons proposé dans un travail antérieur
une condition nécessaire et suffisante permettant de caractériser
les points simples dans une maille cubique 3D, dans le cadre de la
topologie numérique.
Plus concise et plus facile à évaluer que les caractérisations
précédentes, cette caractérisation nécessite uniquement
la recherche de deux nombres de composantes connexes que nous avons
appelés nombres topologiques. Outre la caractérisation
des points simples, les nombres topologiques permettent d'effectuer une
classification des points selon leurs caractéristiques topologiques
locales. Ainsi, il est possible de détecter les points qui ont localement
les mêmes caractéristiques topologiques que des points de
courbes, de surfaces, des points d'intersection de surfaces, de courbes...
Nous avons également proposé plusieurs façons de calculer
ces deux nombres topologiques; par exemple, nous avons montré qu'on
peut calculer ces deux nombres en détectant la présence de
certaines configurations dans le voisinage du point considéré [Ber96].
D'autre part, dans le cadre des ordres,
nous avons introduit les nouvelles notions de
point unipolaire et de point libre, qui sont des
éléments ``inessentiels'' du point de vue de la
topologie.
Nous avons également introduit une définition discrète
de l'homotopie et une généralisation de la notion de point
simple [Ber99] : un point est considéré comme simple si
son voisinage, privé de lui-même, se rétracte en un seul point
(voir Fig. 3).
Il découle de ces notions des algorithmes
parallèles de squelettisation particulièrement élégants et
efficaces (voir la section ``Algorithmes de squelettisation 3D'').
|  |
| (a) | (b)
|
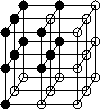
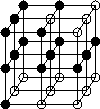
Figure 2: (a): Le point central est simple, (b): le point central
n'est pas simple : s'il est retiré, un trou est localement
créé. Si l'on retire ce point de l'objet (qui peut
s'étendre au delà du voisinage 3x3x3 montré ici) ceci aura
pour effet, soit de créer un trou dans l'objet, soit de
supprimer une cavité de l'objet (voir aussi la section
``Un algorithme de fermeture de trous 3D'').
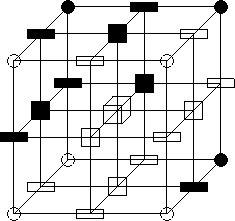
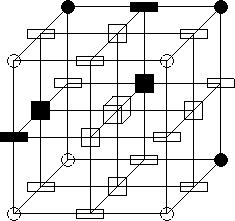
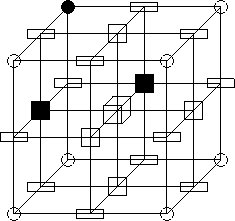
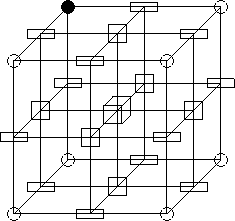
Figure 3: Le point central (figuré par un cube) est simple : son
voisinage, privé de lui même (éléments noirs) peut se
rétracter en un point.