 |
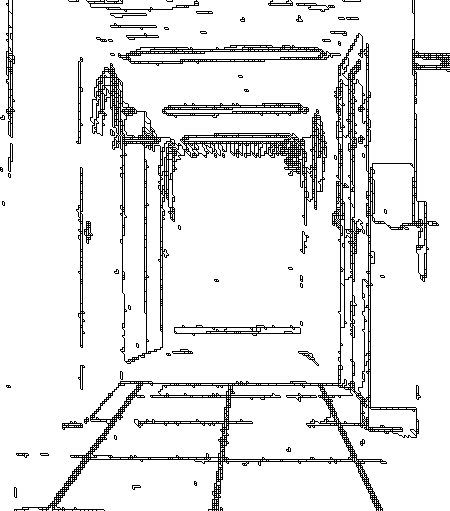 |
| (a) | (b) |
Personnes impliquées : Gilles Bertrand, Michel Couprie, Petr Dokládal.
L'opérateur h-minima est également un outil issu du cadre de la morphologie mathématique. Il permet de filtrer une image en niveaux de gris à partir d'un critère basé sur la ``profondeur'' des minima régionaux : si un minimum a une profondeur inférieure à un seuil h, alors il est éliminé, sinon il est retenu et peut servir de marqueur pour une étape ultérieure de segmentation.
L'application directe de l'opérateur h-minima est limité aux cas où l'on souhaite segmenter l'image en deux classes de pixels (objet/fond), l'objet et le fond pouvant être constitués de plusieurs composantes connexes. Pour appliquer cet opérateur à un problème de segmentation multi-classes, où les régions à segmenter peuvent éventuellement se toucher les unes les autres, on passe classiquement par une image de gradient. Toutefois, les gradients discrets sont délicats à utiliser, en particulier des détails fins de l'image originale peuvent être perdus.
Nous avons proposé un opérateur h-minima agissant sur un graphe valué, qui permet la résolution directe de problèmes de segmentation multi-classes, sans passer par un gradient [DB99]. Ceci nous permet de segmenter des structures fines qui seraient perdues avec l'utilisation de l'approche classique (Fig. 12).
 |
 |
| (a) | (b) |