In many problems related to image processing, topology plays an important role. The notion of continuous deformation which is fundamental in topology, may be introduced in discrete spaces through the notion of simple point: intuitively, a point is simple in an object if it can be withdrawn from this object while preserving its topology. Several mathematical frameworks have been proposed until today, which allow the development of topological notions and operators in discrete spaces. The framework of digital topology, based on the use of two graphs which define the neighborhood relations between object points and between background points, is well adapted to the case of two-dimensional digital images, and also allows to define a notion of simple point in a three-dimensional grid. In this framework, we have proposed a new operator which smoothes 2D and 3D shapes while preserving topology. See the Topological Smoothing home page for more details.

The notion of surface (or manifold in any dimension) is one of most difficult topological notions. We introduced and studied in 1998 the simplicity surfaces, which constitute to our knowledge the most general definition of discrete surface proposed in the framework of digital topology, and which is based on a very natural structural property. With G. Bertrand and X. Daragon (PhD student), we studied different notions of surface in discrete spaces (orders and simplicial complexes). We obtained some new properties in relation to the structure of discrete frontiers. With G. Bertrand and Y. Kenmochi, we showed that a simple discretization scheme, in partially ordered sets, has some interesting properties (in particular: any discrete plane is a discrete surface).

Digital topology was originally proposed for binary images, and until a recent past, no systematic study had been done to generalize its notions to the case of grayscale images. In 1996, G. Bertrand proposed the framework called cross-section topology, he introduced in particular the definition of a destructible point which generalizes the notion of simple point. With G. Bertrand and two PhD students, J.C. Everat and F.N. Bezerra, we have developped this framework by proposing, in particular, new operators which allow to modify the topology of a grayscale image in a controlled manner. Among these operators, a crest restoration operator is particularly original, and compares favorably with respect to classical contour reconnection methods. See the Cross-Section Topology home page for more details.

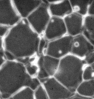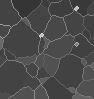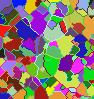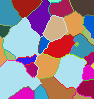
In 1997, we introduced with G. Bertrand the topological watershed, which generalizes the classical watershed notion, and proposed an original algorithm to compute efficiently topological watersheds. This study has been completed recently on the basis of a formal framework, in which important properties have been proved, and which is the subject of several publications. See the Topological Watershed home page for more details.

In discrete grids, producing skeletons that are centered with respect to the Euclidean distance raises difficult problems. In particular, we have do deal with both topological and geometrical constraints, which interact in complicated ways within this framework. In addition, even in the continuous framework the Euclidean skeleton suffers from its sensitivity to small contour perturbations, in other words, its lack of stability. This fact, among others, explains why it is usually necessary to add a filtering step (or pruning step) to any method that aims at computing the skeleton. In the Euclidean skeletons homepage, we present several contributions to the solution of these problems.

Digital topology is effective in dimension 2, but extending its notions to dimension 3 is all but easy. Some "classical" mathematical frameworks, such as simplicial complexes, cellular complexes or partially ordered sets, allow to define a topology in the sense of P.S. Alexandroff, and to obtain some interesting properties; in particular, we proposed a "model" the notions of digital topology in terms of a P.S. Alexandroff topology, and we developped the framework of critical kernels, introduced by G. Bertrand to study the topological properties of parallel thinning algorithms. See the Critical Kernels home page for more details.