SIMPLE POINTS

Topology-preserving operators, such as homotopic skeletonization, are used in many applications of image analysis to transform an object while leaving unchanged its topological characteristics. In discrete grids, a topology-preserving transformation can be defined thanks to the notion of simple point: intuitively, a point of an object is called simple if it can be deleted from this object without altering topology. This notion, pionneered by Duda, Hart, Munson, Golay and Rosenfeld in the late 60s, has since been the subject of an abundant literature. In particular, local characterizations of simple points have been proposed, on which efficient implementation of thinning procedures are based.

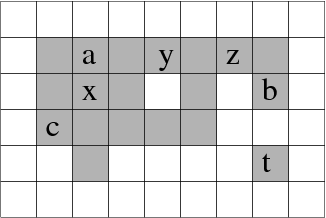
Let us illustrate informally the notion of simple point through some examples, first in 2D, then in 3D. In Fig. 1, the points (or pixels) x,y,z,t are not simple: the removal of x from the set X of pixels would create a new connected component of the complement X^c of X ; the removal of y would merge two connected components of X^c ; the removal of z would split a connected component of X ; and the removal of t would delete a connected component of X. On the other hand, the pixels a, b and c are simple pixels. We see that, in 2D, the notion of connectedness (for both X and X^c) suffices to characterize simple pixels.

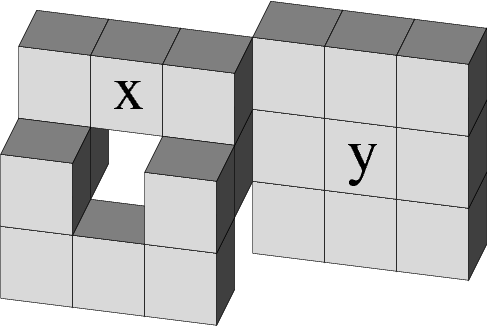
Things are more difficult in 3D. Consider the example of the set X depicted in Fig. 2, removing the voxel x or the voxel y from X would not split, merge, create or suppress any component of X nor any component of X^c. However neither x nor y is simple, for the deletion of x (resp. y) causes the suppression (resp. creation) of a tunnel. Surprisingly, it is still possible to characterize 3D simple points by local conditions which are only based on connectedness, but connectedness alone is not sufficient to characterize 4D simple points.