CRITICAL KERNELS: OVERVIEW
Since the first parallel thinning algorithm proposed by Rutovitz in 1966, several attempts have been made to formalize and understand the conditions under which a process that simultaneously remove points from a discrete objects can be guaranteed to preserve topology. The minimal non-simple sets introduced by C. Ronse (1988), the P-simple points due to G. Bertrand (1995) are main steps of this research. Meanwhile, many authors have proposed and published incorrect skeletonization algorithms. This fact illustrates both the difficulty of the problem (even in 2D; see [Cou06]) and the importance of beeing able to exhibit formal proofs.
In [Ber07], we introduce a general framework for studying parallel homotopic thinning in spaces of any dimension, in the context of abstract simplicial or cubical complexes. We propose a new definition of a simple point, this definition is based on the collapse operation, a classical tool of algebraic topology which allows to guarantee topology preservation. Furthermore, we generalize the notion of simple point by the one of critical face, and we define the critical kernel of an object as the set of all its critical faces. The most fundamental result of [Ber07] is that, whenever an arbitrary subset Y of an object X contains the critical kernel of X, then Y has the same topology as X (see Fig. 1, Fig. 2).
 |
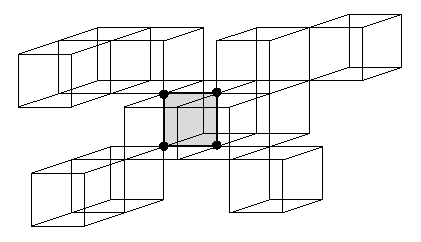 |
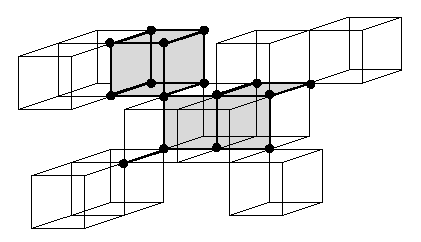
Figure 1. Left: an object X and its critical kernel. Right: the critical kernel of the critical kernel of X, an ultimate skeleton.
 |
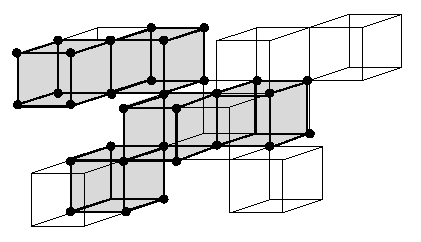 |
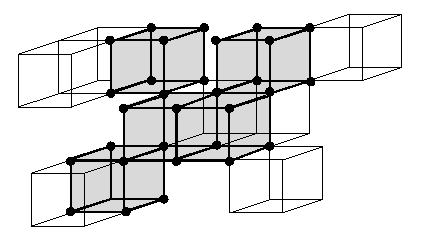
Figure 2. Two voxel sets from X which contain the critical kernel of X: both have the same topology as X.
This result leads indeed to a broad class of parallel thinning algorithms, which all have the property of topology preservation ``built in''. The very notion of critical kernel can be seen as a thinning algorithm, which consists in computing iteratively the critical kernel of the preceding computation (see Fig. 1). In addition, the possibility to choose arbitrarily any subset Y between X and its critical kernel allows us to add some geometrical constraints to the thinning process, and to obtain new 3D skeletons, for example curvilinear or surfacic skeletons [BC06c], or skeletons guided by the Euclidean distance [CSB06].
Even in the 2D case, for which hundreds of thinning methods have been published, we were able to propose in [BC06a,BC06b] nine original algorithms, with properties which have no equivalent in the literature. Thanks to local characterizations of critical faces, these algorithms are computationally efficient, and need no explicit representation of objects in terms of cubical complexes, for they can be expressed in a very simple manner by the way of masks in Z² or Z³.
We demonstrated in [BC09] that the main concepts previously introduced in order to study topology-preserving parallel thinning in the framework of digital topology, namely P-simple points and minimal non-simple sets, may be retrieved, better understood and enriched in the framework of critical kernels.
More precisely, P-simple points and minimal simple sets are particular cases in the critical kernels framework, which thus appear to constitute a unifying framework which encompasses previous works on parallel thinning.
Furthermore, in contrast with minimal non-simple sets, critical kernels provide a methodology to produce thinning algorithms which preserve topology "by construction", and we showed in [BC09] that these algorithms are more powerful than those which may be designed on the basis of P-simple points.
Site info
© 2006-2007 A2SI Lab.
