Topological watershed: overview
The notion of watershed appeared in the XIXth century with, in particular, the works of J.C. Maxwell. Since the 1980s, it has been the topic of numerous studies, mainly motivated by applications in image analysis. Indeed, the watershed constitutes one of the main concepts of Mathematical Morphology, and in this framework, it is considered as one of the most powerful operators allowing to segment an image.
Nevertheless, to our best knowledge, there was no formal framework allowing for a precise definition of the watershed in a discrete space, and for demonstrating some properties. On the contrary, some properties that we consider as essential were not satisfied by the existing operators. In particular, these operators do not preserve the ``contrast'' of the image, the lines obtained by these operators can be wrongly positioned...
The aim of this work is to show that such a framework exists and that
the topological approach of the watershed proposed in
[CB97] allows, not only to satisfy these
fundamental properties, but also to obtain several non-trivial theorems.
In particular, in [Ber05] we prove that a function
W is a watershed of a function F if and only if
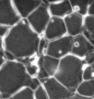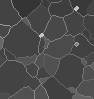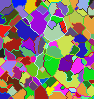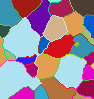
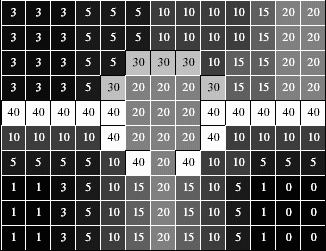
W ≤ F and W preserves the contrast between the regional minima of F;
where the contrast between two regional minima M and M' is defined as the
minimal altitude to which one must climb in order to go from M to
M' (see Fig. 2).
This result is a very striking one, for comparison, it is not possible
to obtain such a characterization in the framework of ``classical''
topological transformations (homotopic transforms).
 |
 |
 |
 |
Algorithms
In [CNB05], we study algorithms to compute topological watersheds. We propose and prove a characterization of the points that can be lowered during the computation of a watershed, which may be checked locally and efficiently implemented thanks to a data structure called component tree (see [NC06]). This leads to a quasi-linear algorithm, which is proved to give correct results with respect to the definitions.
Watersheds and region merging
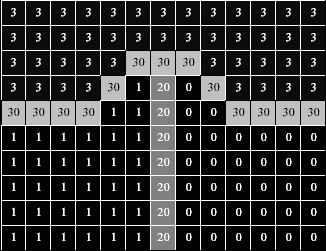
Region merging methods consist of improving an initial segmentation by merging some pairs of neighboring regions. In [CBCN08], we consider a segmentation as a set of connected regions, separated by a frontier. If the frontier set cannot be reduced without merging some regions then we call it a (binary) watershed. In a general graph framework, merging two regions is not straightforward (see Fig. 3). We define four classes of graphs for which we prove, thanks to the notion of watershed, that some of the difficulties for defining merging procedures are avoided.
Our main result is that one of these classes is the class of graphs in which any binary watershed is thin. None of the usual adjacency relations on Z2 and Z3 allows a satisfying definition of merging. We introduce the perfect fusion grid on Zn, a regular graph in which merging two neighboring regions can always be performed by removing from the frontier set all the points adjacent to both regions.
The previous results were related to "binary" watersheds, also called clefts. In [CCNB07], we extend this study to the case of grayscale watersheds.
 |
 |
 |
 |
| (a) | (b) | (c) | (d) |
On the dynamics
The notion of dynamics, introduced by Michel Grimaud, is a measure associated to each regional minimum of a function (or a grayscale image). Intuitively, this measure corresponds to the ``depth'' of a minimum. The dynamics can be used to eliminate, in an image, those minima which are not significant (which are only due to noise).
In [Ber05a,Ber07] we propose a new definition of the dynamics which is, to our view, more relevant than the original one. This new definition allows, in particular, to obtain interesting properties. For example, we proved the equivalence between an operator which preserves the dynamics of a function and an operator which preserves the topological watershed. We also proved such an equivalence with an operator which preserves a certain minimum spanning tree which can be extracted from a function.
Mosaics and emergence
The most classical approach to compute watersheds consists in simulating the flooding of a topographical relief. In [NCB05], we investigate the links between the flooding paradigm, and the topological watershed. Guided by the analysis of a classical flooding algorithm, we present several notions that lead us to a better understanding of the watershed; in particular, we introduce the mosaic to retrieve the altitude of points along a divide set. A desirable property is that, when two minima are separated by a crest in the original image, they are still separated by a crest of the same altitude in the mosaic. Our main result in this work states that it is the case if and only if the mosaic is obtained through a topological thinning. We investigate the possibility for a flooding to produce a topological watershed, and conclude that this is not feasible.
This leads us to reverse the flooding paradigm, and to propose a notion of emergence. An emergence process is a transformation based on a topological criterion, in which points are processed in decreasing altitude order while preserving the number of connected components of lower cross-sections. Our main result states that any emergence watershed is a topological watershed, and more remarkably, that any topological watershed of a given image can be obtained through an emergence process.
Watersheds in edge-weighted graphs
In [CBNC08], we study the watershed in edge-weighted graphs. We define the watersheds following the intuitive idea of drops of water flowing on a topographic surface. We establish the consistency of these watersheds and prove their optimality in terms of minimum spanning forests. We introduce a new local transformation on maps which equivalently define these watersheds and derive two linear-time algorithms. To our best knowledge, similar properties are not verified in other frameworks and the two proposed algorithms are the most efficient existing algorithms, both in theory and practice.
Site info
© 2006-2007 A2SI Lab.