Affectation optimale de tâches sur des processeurs répartis : méthode de recuit simulé

Personnes impliquées : Yskandar Hamam

L'affectation optimale de tâches sur les processeurs d'un système réparti est un problème dont la résolution effective est importante durant toutes les phases du développement de tels systèmes. Au cours de la phase de conception, elle permet d'aider à la détermination de la configuration permettant d'atteindre un niveau de performance souhaité ; pendant la phase de fonctionnement, elle facilite l'optimisation des ressources disponibles ; au cours d'une reconfiguration, elle aide à la réaffectation des modules en fonction des changements affectant le système.

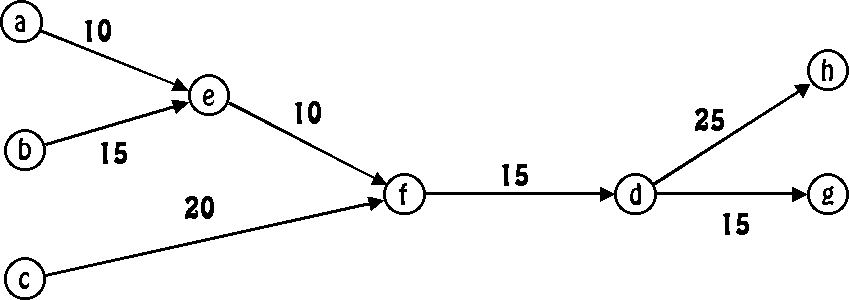
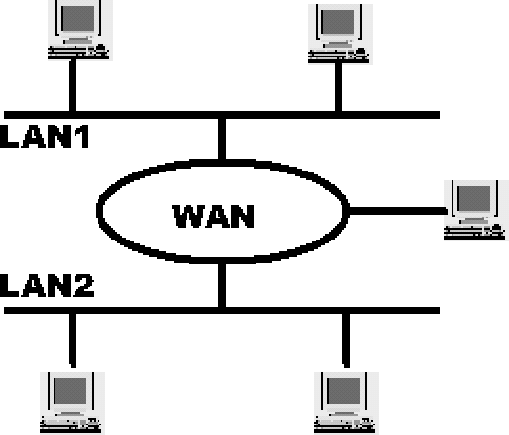
Le problème peut être représenté par deux graphes comme on peut le voir sur la figure ci-dessous. Le graphe des tâches montre les interdépendances entre tâches et les taux des transferts d'informations associés. L'autre graphe correspond au réseau sur lesquels les processeurs sont connectés.


(a)		(b)

Figure 3: (a) Un exemple de graphe de communication entre tâches. (b) Un exemple de réseau de communication.

Le problème, dans ses diverses versions, fait l'objet d'une littérature importante en configuration des systèmes parallèles et multi-processeurs. Les algorithmes existants appartiennent aux catégories suivantes :

algorithmes exacts appliqués à des problèmes simplifiés ;
algorithmes heuristiques sous-optimaux appliqués aux problèmes complets ou simplifiés ;
algorithmes exacts appliqués aux problèmes complets.

Cependant, le problème étant NP-complet, sa résolution exacte utilisant par exemple un schéma de type séparation et évaluation n'est pas envisageable pour des problème d'une taille réelle. C'est pourquoi l'utilisation du recuit simulé (qui a démontré sa réelle capacité à trouver des solutions quasi-optimales dans beaucoup de problèmes d'optimisation combinatoire) est largement justifiée. Nous avons donc résolu ce problème en utilisant le recuit simulé, méthode dont nous avons une longue expérience. En outre, des approches de type séparation et évaluation appliquées à ce genre de problèmes sont disponibles dans la littérature. Elles sont essentiellement basées sur la résolution d'un problème non linéaire d'évaluation. A l'heure actuelle nous développons notre propre approche de type séparation et évaluation mais à partir d'une reformulation linéaire du problème.

Dernière mise à jour : par François Rocaries.