



Points P-simples et algorithmes de squelettisation 3D parallèles
Personnes impliquées : Gilles Bertrand, Laurent Perroton.
Par définition, on peut enlever un point simple sans modifier
la topologie d'un objet.
Cependant la suppression en parallèle de
points simples peut changer la topologie d'un objet (Fig. 5).
En 2 dimensions, certaines
approches ont été proposées pour résoudre ce
problème : l'une des plus utilisées consiste à classer les
points dans quatre catégories, les points de type nord, sud, est, ou
ouest. A chaque itération, seuls les points d'un type donné
peuvent être candidats pour la suppression.
Cependant cette approche n'est plus valable dans un
espace à trois dimensions, comme le montre la Fig. 5:
en effet, on doit maintenant considérer les six directions
nord, sud, est, ouest, haut, bas,
et les points x et y sont tous deux du type haut.
A travers la notion de point P-simple,
nous proposons une stratégie générale pour enlever
des points en parallèle sans changer la topologie. Cette notion
de point P-simple correspond a une notion d'homotopie forte: un ensemble
Y est fortement homotope à un ensemble X, si Y est inclus dans X
et si pour tout Z, tel que Y inclus dans Z et Z inclus dans X,
Z est homotope à X. Dans ce cas P = X \Y est constitué
de points dits P-simples (voir Fig. 6).
Nous avons proposé une caractérisation des points P-simples
qui peut être effectuée en un temps linéaire. Le problème
que nous avons résolu était à priori exponentiel,
ce résultat est donc tout à fait inespéré
[ Ber95b , Ber95c ].
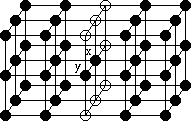
Figure 5: Un objet composé de deux parallélépipèdes
``reliés'' par deux points x et y :
les points x et y sont tous deux simples, cependant
ils ne peuvent être supprimés en parallèle sans changer la
topologie.
 |
 |
| (a) | (b)
|
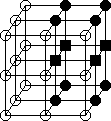
Figure 6: Les disques noirs représentent les points de Y = X \P, et les carrés
noirs les points de P.
(a): Le point central est P-simple, (b): le point central x n'est pas P-simple,
car en enlevant certains points de P, on peut rendre x non simple.



