Greedy algorithms

In this chapter we are interested in solving optimization problems. In such kind of problems, we have

• a space of feasible solutions, i.e. possible answers satisfying the constrains of the problem, and

• a function associating a weight (or score, or error…) to each feasible solution.

The goal is then to find a solution whose weight is minimum (or maximum): this is called an optimal solution. There might be several optimal solutions and we usually just want to find any one of them.

In greedy algorithms, the solution is constructed incrementally:

• We start with the empty partial solution.

• At each step, we make the choice that seems to be the best and we add it to the current partial solution.

Let’s see how this work with a simple real life problem: the change-making problem. Assume that we have different coin values \(\{1,2,5,10,20,50,100,200\}\), the change-making problem is to find the minimum number of coins that add up to a given amount of money.

For example if a cashier has to return 86, 2 feasible solutions are:

• 8 coins of value 10 and 3 coins of value 2, the weight of this solution is 11 (total number of coins), or

• 4 coins of value 20, 1 coin of value 5, and 1 coin of value 1, the weight of this solution is 6.

The second solution is better than the first one, because the cashier uses less coins. It is however not an optimal solution. This problem can be solved by the following greedy approach:

• We start with 0 coin (this is the empty partial solution), the amount we still have to give back is \(x\)

• While \(x>0\):

  • Find the coin with the largest value that is smaller than \(x\). This is the choice that seems the best at the moment.

  • Add this coin to the partial solution. We increase the size of the partial solution.

  • Subtract the coin value from \(x\). Making the change for the new value of \(x\) is our new sub-problem.

Applying this strategy to the previous example produces the following steps:

Solution	Number of coins	x
\(\{\}\)	0	86
\(\{50\}\)	1	36
\(\{50,20\}\)	2	16
\(\{50,20,10\}\)	3	6
\(\{50,20,10,5\}\)	4	1
\(\{50,20,10,5,1\}\)	5	0

We obtain, a solution which is made up of 5 coins. Here, the greedy approach is very natural, at each step, we just take the coin that provides the best improvement in our solution, i.e. the one that enables to decrease the most the amount of change we still have to return.

For this problem, with this set of coins, we can indeed show that the greedy approach is optimal: the solution returned by the algorithm is an optimal solution (in this case it is indeed the only optimal solution).

Propose a linear algorithm to solve the change-making problem with the greedy strategy.

Programming exercise : Implement change making in the python notebook

You are a thief in a grain store. Your bag can contain a maximum of \(k\) kg of grain. On the shelves there are several bags of grain \(g_i\), each bag has a different weight \(w_i\) and a price \(v_i\). Your goal is to maximize the value of the grains your are going to steal. You can open a bag of grain and only take a fraction of it. This problem is known as the fractional knapsack problem.

Propose a greedy algorithm to solve this problem, i.e. tell which quantity of which grain should be stolen to maximize your profit. Clearly state what are the inputs of your algorithm and the output.

Not all problems can be solved by greedy algorithms

The greedy approach is often appreciated for its simplicity and effectiveness. Unfortunately, it is in general not able to provide optimal solutions.

For example, let consider a simple variation of the above change-making problem: assume that we have an extra coin to our coin set with the value 40. The coin set becomes \(\{1,2,5,10,20,40,50,100,200\}\).

If we use our greedy algorithm to find how to make 86 with this new coin set, we find the same decomposition as above \(\{50,20,10,5,1\}\). However, we can see that the decomposition \(\{40,40,5,1\}\) is indeed better than the one provided by the greedy algorithm: it uses only 4 coins while the other uses 5. The greedy algorithm fails to give an optimal solution with this set of coins.

Let consider a second example which is a variation around the famous traveling salesman problem. We have a set of cities \(\{C_0, C_1, \ldots, C_n\}\) and roads linking two cities. Each road has a weight which corresponds to a travel time. At the beginning, we are in the city \(C_0\) and the goal is to find a path visiting all the cities with the minimum travel time. In other word, a solution to this problem is a sequence of cities \((x_0, \ldots, x_m)\) such that

• \(x_0 = C_0\): we start from \(C_0\);

• for any \(i\), there is a road linking \(x_i\) to \(x_{i+1}\): there must be a direct link between to adjacent cities in the sequence;

• for any city \(C_j\), there exists \(i\) such that \(x_i=C_j\): we visit all the cities in the solution.

Then the weight of a solution is the sum of the weights of the roads between \(x_i\) to \(x_{i+1}\) for any \(i\). In other words, it is the total travel time to visit all the cities in the order given by the sequence.

Consider the following cities and roads configuration:

Fig. 24 In this figure, each circle represents a city. A line between two cities is a road and the number near the line indicates the travel time for this road. For example, we can go from city \(C_0\) to city \(C_2\) in 3 units of time. However, we can not go directly from \(C_0\) to \(C_3\): there is not direct road and we have to find a path (traverse other cities) to do this.

A possible solution for this configuration is \(C_0, C_1, C_2, C_5, C_4, C_3\); the weight of this solution is \(1+3+8+2+2=16\).

What is the weight of the optimal solution to the problem depicted in Fig. 24?

A greedy strategy for this problem is called the nearest neighbor strategy: to chose the next city to visit we simply take the closest one.

Applying this strategy to the previous example, gives the following steps:

Solution	weight
\(\{C_0\}\)	0
\(\{C_0, C_1\}\)	1
\(\{C_0, C_1, C_3\}\)	3
\(\{C_0, C_1, C_3, C_4\}\)	5
\(\{C_0, C_1, C_3, C_4, C_5\}\)	7
\(\{C_0, C_1, C_3, C_4, C_5, C_2\}\)	15

The solution \(\{C_0, C_1, C_3, C_4, C_5, C_2\}\) given by the greedy approach has a weight of 15. However, the optimal solution is \(\{C_0, C_2, C_1, C_3, C_4, C_5\}\) which has a weight of 12, the greedy approach thus failed to find an optimal solution.

Here we can easily understand what happened: at the first step, the greedy approach wants to visit \(C_1\) because it is the closest and then \(C_2\). But, at this point we are somehow trapped because, in the future, we will now have to take the road from \(C_5\) to \(C_2\) which is costly. In order to avoid this road in the future, we have to make a choice that is locally non optimal at the beginning: first visit \(C_2\).

In other words, there are problems where we have to accept to lose at some point in order to have a larger gain later: greedy algorithms are generally not able to find an optimal solution for those problems.

Activity selection problem

Let’s see a more complex example in details. Suppose you are in charge of allocating slots in one of the school’s lecture halls. For each day, you receive several reservation requests each with a start time \(s_i\) and a finish time \(f_i\). Unfortunately, you cannot accept all the reservations as some are overlapping (for example activity \(k\) wants to starts while activity \(\ell\) has not yet finished). You thus have to select a subset of activities that do not overlap: this is called a feasible solution. Of course there are many possible solutions, and you decide that a fair approach would be to maximize the number of satisfied requests: in other words, an optimal solution is a solution which contain the maximum number of reservations.

Fig. 25 Example of an activity selection problem. On the interval of time going from 8 to 20, you received 7 reservation requests each with a start time \(s_i\) and a finish time \(f_i\). You cannot accept two overlapping activties. Which activities should you accept in order to maximize the numbre of accepted activites?

The activity selection problem can indeed be solved efficiently with a greedy approach:

• start with an empty solution (no activity selected).

• at each step: select the activity which does not conflict with already selected activities and which has the earliest finish time.

In other words, the greedy choice is the one that leaves the resource available for the longest time, which is indeed quite intuitive as the goal is to maximize the number of accepted requests.

Propose an efficient algorithm in pseudocode solving the activity slection problem with the greedy strategy.

With \(n\) the number of activities, the time complexity of this algorithm is Θ()

Programming exercise : Implement activity selection in the python notebook

Correction

Now, an interesting question is: does the greedy strategy provides an optimal solution to the activity selection problem? If yes, how can we prove it?

The answer is yes, the solution given by the greedy strategy is optimal. The idea of the proof relies on two elements:

1. Greedy choice property: we want to show that the greedy choice is always a valid first choice. To show this we are going to consider an optimal solution to the problem and we will see that replacing the first activity of this solution by the greedy choice still gives an optimal solution

2. Optimal substructure property: we want to show that an optimal solution to the problem contains an optimal solution to the sub-problem obtained by removing the first element of the solution from the problem.

With these two elements – greedy choice property and optimal substructure –, we can show recursively that any activity of an optimal solution is either: an activity selected by the greedy choice, or can be replaced without harm (the new solution is still optimal) by the activity selected by the greedy choice.

Formally, let \(S=\{1,2,\ldots ,n\}\) be the set of activities ordered by finish time. Let \(A=\{a_1,\ldots,a_m\}\subseteq S\) be an optimal solution, also ordered by finish time. Note that, as the activities are sorted by finish times, the first activity chosen by the greedy strategy is the activity 1.

Greedy choice property: Let’s look at the first activity \(a_1\) of the optimal solution \(A\).

• If \(a_1=1\), the first activity of \(A\) corresponds to the greedy choice.

• If \(a_1\neq 1\), let consider the new set of activities \(B=\{1, a_2, \ldots, a_m\}\). Note that, the finish time of activity 1 is smaller than or equal to the finish time of \(a_1\) (as the activities are sorted by finish time): the activities in \(B\) are thus not overlapping and \(B\) is a valid solution. The solution \(B\) also has the same number of activities as the optimal solution \(A\), it is thus also optimal.

Optimal substructure property: Therefore, in both cases, we have found an optimal solution that starts with the greedy choice, let’s call it \(C\) (in case 1, \(C\) is indeed \(A\) and in case two, \(C\) corresponds to \(B\)). We can now reduce the problem to a sub-problem by removing this first activity from the solution \(C\) and all the conflicting activities from \(S\). Let \(C^{\prime} = C \setminus \{1\}\) and let \(S^{\prime}=\{i\in S:s_{i}\geq f_{1}\}\) (\(S^{\prime}\) is the set of activities of \(S\) which starts after the end of the first activity, the one chosen by the greedy choice). Then, the set \(C^{\prime}\) is an optimal solution to the sub-problem \(S^{\prime}\): this can be proven by contradiction. Assume that there exists a solution \(D\) to \(S^{\prime}\) with more activities than \(C^{\prime}\), then \(D \cup \{1\}\) would be a solution to \(S\) with more activities than \(C\), which is in contradiction with the fact that \(C\) is an optimal solution of \(S\).

Conclusion: Because the exact same reasoning applies to the subproblem \(S^{\prime}\) with the optimal solution \(C^{\prime}\) and recursively to its sub-sub-problems, we can state that the optimal solution \(A\) is indeed made of greedy choices or that any of its activity that does not correspond to a greedy choice can be replaced by the greedy choice while preserving the optimality of the solution. The solution made only of greedy choices is thus optimal.

Instead of taking the activity with the least finish time, one could have thought of other greedy strategies for the activity selection problem sub as:

• Select the activity which does not conflict with already selected activities and which has the earliest start time; or

• Select the activity which does not conflict with already selected activities and which has the least duration; or

• Select the activity which does not conflict with already selected activities and that overlaps the fewest other remaining activities.

For each of these greedy strategies, find a counter-example showing that it does not produce an optimal solution.

Kermit the Frog is sitting on a stone in the middle of the river. Kermit wants to join its friend, Hypno Toad, who is waiting on another stone down the river. Kermit will have to jump from stone to stone to reach its friend: its goal is to reach Hypno Toad by making the least possible jumps.

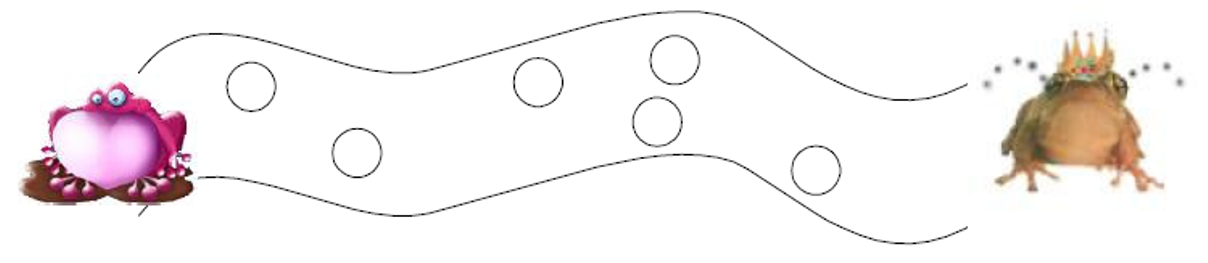
Fig. 26 Illustration of Kermit’s problem (source Lilian Buzer).

The problem is encoded as follows. Stones are numbered from 0 to \(n\). Kermit is on stone 0 while Hypno is on stone \(n\). For each stone \(i\), the value \(delta[i]\) indicates the furstest stone that can be reach by Kermit by jumping from the stone \(i\). In other words, when Kermit is on the stone \(i\), it can jump on the stones \(i\), \(i+1\), …, \(delta[i]\). When Kermit is on a stone \(i\) located between the stones \(k\) and \(\delta[k]\), Kermit can at least jump up to \(\delta[k]\). In other words, \(\forall i<j, \delta[i]\leq \delta[j]\).

1. Propose a greedy algorithm to solve Kermit’s problem.

2. Show that your solution is optimal.

A fraction is a unit fraction if its numerator is equal to 1. Any fraction can be written as a sum of unit fractions. An Egyptian fraction is a decomposition of a fraction as a sum of unit fractions that uses as few terms as possible. For example, we have the following decompositions:

Fraction	Egyption fraction representation
\(\frac{2}{3}\)	\(\frac{1}{2} + \frac{1}{6}\)
\(\frac{12}{13}\)	\(\frac{1}{2} + \frac{1}{3} + \frac{1}{12} + \frac{1}{156}\)

Note that, given a fraction \(\frac{a}{b}\), with \(0<a<b\), the smallest integer \(c>0\) such that \(\frac{a}{b}\geq\frac{1}{c}\) is \(\left\lceil \frac{b}{a} \right\rceil\) (where \(\lceil x \rceil\) is the ceil of \(x\), i.e. the smallest integer greater than or equal to \(x\)).

1. Propose a greedy algorithm that, given 2 integers \(0<a<b\), prints an Egyptian fraction decomposition of \(\frac{a}{b}\).

2. Implement Egyptian fraction in the python notebook.

Huffman coding

Huffman coding is a way to efficiently compress data. The idea of Huffman coding is to construct a variable length binary encoding of symbols according to their frequency: a symbol that appears frequently in the data to be encoded should be represented by a short binary sequence. The binary sequence used to encode a symbol is called a codeword or simply a code.

For example, consider that we have a string of size 100 containing only the characters “abcd”. As there are 4 different symbols, a fixed-length code requires 2 bits per symbol (\(\log_2(4)\)). The frequency of apparition of each symbol in the string and possible fixed-length and variable length encoding are given in the table below:

	a	b	c	d
Frequency	50	10	12	28
Fixed-length code	00	01	10	11
Variable-length code	0	100	101	11

With the fixed length code, encoding the string requires \(100*2=200\) bits. With the variable length code, we need \(50*1 + 10*3 + 12*3 + 28*2=172\) bits. Thus despite using more bits to encode some characters, we managed to save 28 bits (14% compression ratio) in this example. In real life use cases, the compression ratio obtained with variable-length code can reach much higher rates.

Prefix code

Decoding fixed-length code is easy: for a code of length \(n\), we just have to split the binary encoded sequence in blocks of \(n\) bits and find the symbol associated to each block. This is obviously not possible with a variable-length code: we cannot know in advance where the code of each symbol starts and stops in the encoded binary data. Indeed, variable-length code must satisfy what is called the prefix code property in order to be decoded.

A code is a prefix code if for any two codewords \(w_i\) and \(w_j\), \(w_i\) is not a prefix of \(w_j\). In other words, a codeword is never the beginning of another codeword. For example, the variable-length code given in the table above is a prefix code as:

• 0 is a code and there is no other code starting by 0

• 100 is a code and there is no other code starting by 100

• 101 is a code and there is no other code starting by 101

• 11 is a code and there is no other code starting by 11

On the contrary, the variable-length code {a: 0, b: 01, c: 10, d: 100} is not a prefix code as the code for a is a prefix of the code for b (the code for b “01” starts with the code for a “0”).

Prefix code are easy to decode. Since no codeword is a prefix of another, the first codeword in an encoded binary data is non ambiguous. We can then identify the first codeword, decode it, and repeat this process on the remainder of the binary data.

For example, consider the binary sequence 100110010000 which is encoded with the variable-length prefix code given in the table above.

• The first codeword of 100110010000 can only be 100 which is a “b”, the remaining sequence is 110010000.

• The first codeword of 110010000 can only be 11 which is a “d”, the remaining sequence is 0010000.

• The first codeword of 0010000 can only be 0 which is a “a”, the remaining sequence is 010000.

• …

Code as binary trees

A binary tree is a data-structure composed of nodes. Each node contains 3 elements:

• an attribute value or weight: this can be any data useful to describe the node content;

• a left child: this is a reference to another node, it can be empty; and

• a right child: this is a reference to another node, it can be empty.

Fig. 27 Example of binary tree with 7 nodes. The node 0 has two children, the node 1 is its left child and the node 2 is its right child. If a node \(m\) is a child (left or right) of a node \(n\), then we say that \(n\) is the parent of \(m\). The node 0 is the parent of the node 1. A node which has no parent is called a root: the node 0 in blue is a root. A node which has no child is a called a leaf: the red nodes are leaves. The depth of a node \(n\) is equal to length of the path between \(n\) and the root: for example, the depth of the node 6 is equal to 3 and the depth of the node 3 is equal to 2.

We can represent a variable-length code by a binary tree, where symbols are leaf nodes and parent-child relations represent 0 or 1. For example the variable-length code described above can be represented by the following binary tree.

Fig. 28 The leaves (rectangle) represent the symbols; the value inside a leaf node is the frequency of the character. The value inside non-leaf nodes is equal to the sum of the frequency of the symbols below this node in the tree. The code of a symbol is given by the 0s and 1s along the path from the root to the leaf corresponding to this symbol. For example, to go from the root to the symbol “c”, we have first to follow the right child of the root (1), then, we take the left child (0), and finaly the right child (1): the code for “c” is thus 101. Note that the depth of a leaf node is equal to the length of the code of the symbol it represents.

Assume that you are given a binary tree representing a variable-length prefix code and a string of 0s and 1s. Propose an algorithm to decode the first symbol in the string.

Assume that you are given a binary tree representing a variable-length prefix code, propose an algorithm that creates a dictionary associating each symbol in the tree to its codeword.

Hint: a stack or a queue may help you.

Given a binary tree \(T\) representing a variable-length prefix code and a sequence of symbols \(S\), we can compute the number of bits required to encode this sequence. Let \(freq(s)\) be the frequency (number of appearance) of the symbol \(s\) in the sequence. Let \(depth(s)\) be the depth of the node representing the symbol \(s\) in the tree \(T\). The number of bits required to encode the sequence is then equal to the sum over every possible symbols \(s\) of the frequency of \(s\) multiplied by the depth of \(s\). We call it \(W_S(T)\) the weight of the tree \(T\) for the sequence \(S\):

\[W_S(T) = \sum freq(s)*depth(s).\]

Huffman code

Huffman proposed a greedy strategy to find for any sequence \(S\), a tree \(T\) representing a variable-length prefix code of minimum weight for \(S\). In other words, it construct a tree that will minimize the number of bits required to encode the sequence. The greedy strategy is described as follows:

• For each symbol \(s\) in \(S\), create a node whose weight is equal to the frequency of \(s\) in \(S\).

• While there are more than 1 root node:

  • Find the two root nodes \(n_1\) and \(n_2\) with the smallest weight.

  • Create a new node whose children are \(n_1\) and \(n_2\) and whose weight is equal to the sum of the weights of \(n_1\) and \(n_2\).

Fig. 29 Application of the Huffman greedy strategy to the first example. In the first step, we construct a leaf node for each symbol, the weight of the node is the frequency of the symbol. At step 2, we find the two root nodes with the smallest weights, which are the nodes representing the symbols “b” and “c”, we create a new node whose children are “c” and “d” and whose weight is the sum of the weight of “c” and “d”. At step 3, we find again the two root nodes with the smallest weights, which are the nodes representing the symbols “bc” and “d”, we create a new node whose children are “bc” and “d” and whose weight is the sum of the weight of “bc” and “d”. At step 4, we find again the two root nodes with the smallest weights, which are the nodes representing the symbols “bcd” and “a”, we create a new node whose children are “bcd” and “a” and whose weight is the sum of the weight of “bcd” and “a”. Now only one root node remains and the algorithm ends.

Propose an efficient algorithm for Huffman greedy algorithm. The input of the algorithm is the list of symbols \(s_i\) and their frequency \(f_i\). The time complexity of your algorithm must be \(\Theta(n\log(n))\) with \(n\) the number of symbols.

Proving that Huffman greedy strategy is optimal is a bit more involving than with the activity selection problem but let’s see a sketch of the proves.

Greedy choice property: Assume that we have a sequence \(S\) and a tree \(T\) representing a variable-length prefix code optimal for \(S\). Let \(s_1\) and \(s_2\) be the two symbols with the lowest frequency (the ones chosen by the greedy choice). If the depth of \(s_1\) and \(s_2\) is maximal in \(T\) and if they have the same parent, then this means that \(T\) contains the first greedy choice. Otherwise, we can show that \(T\) can be modified such that the depth of \(s_1\) and \(s_2\) is maximal in \(T\) and that they have the same parent while still having an optimal tree. The idea is to swap the leaves representing \(s_1\) and \(s_2\) with two leaves nodes of maximal depth that have the same parent. Indeed, by doing so, the depth of \(s_1\) and \(s_2\) can increase, so the product \(freq(s_1)*depth(s_1)\) and \(freq(s_2)*depth(s_2)\) can increase too. However if the depth of \(s_1\) (or \(s_2\)) increases, that means that the depth of the other symbol \(s_i\) in the swap decreases and as, by hypothesis the frequency of \(s_i\) is greater than the frequency of \(s_1\), then the decrease of \(freq(s_i)*depth(s_i)\) will compensate the increase of \(freq(s_1)*depth(s_1)\). In the end, the weight of the new tree cannot be greater than the weight of the original tree: the new tree that contains the first greedy choice is optimal.

Optimal substructure property: After each step of the greedy Huffman method, we indeed address a new subproblem where the two less frequent symbols \(s_1\) and \(s_2\) have been replaced by a virtual symbol that represent their union. In the tree this corresponds to the parent node of the two selected symbols \(s_1\) and \(s_2\). If the tree \(T\) is optimal for the original sequence then, the tree \(T^{\prime}\) obtained by removing the two leaf nodes representing \(s_1\) and \(s_2\) is optimal for the subproblem where \(s_1\) and \(s_2\) are merged. As in the activity selection problem, this can be shown by contradiction: if \(T^{\prime}\) is not optimal for the sub-problem, then there exists an optimal solution \(T^{\prime\prime}\) for the sub-problem and we can construct a new tree \(U\) from \(T^{\prime\prime}\) that is a better solution to the original problem than \(T\), contradicting the hypothesis that \(T\) is optimal.

Implement Huffman coding and decoding in the python notebook.

The project contains a Node class used to represent binary trees. In practice a tree will be given by its root node.