First we will try to find a continuous transfer function (using Laplace Transform) equivalent to our discrete model. For this purpose we will use the well known bilinear transformation giving the discrete model from the continuous model. Let s be the Laplace Transform we get:
![]()
Where h is the sampling period. Thus we obtain for z:
![]()
And for example the model describe by equation 4 become:
In fact we can neglect the term in ![]() on the numerator to obtain:
on the numerator to obtain:
and if we compare the result obtain by the simulation of the the 3 systems describe by 4, 5 and 6, we obtain the next figure (7)
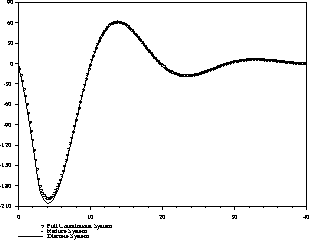
Figure 7: Comparison between the 3 Models
The mechanical equivalent of this transfer function will be a very simple system with a inertia a friction and a elasticity. The mass of the dispositif has to be the essential part of the system and will determine the desired value for the other coefficients -friction and elasticity-, to take in account the amplitud difference between the response we have probably to increase with the volumen the friction and or the elasticity. In order to take in account the decreasing of the upper bound of our linear filter we just have to consider that the friction and the elasticity of our model are changing with the volumen of the balloon. It's not really difficult to explain this comportment if we try to think in term of biomechanical comportment. In fact the elasticity and the distension possibility of the muscle are bounded and the normal mechanical resistance of rectal lining will probably increase too with the volumen of the balloon. This recording could be very helpful to establish (if necessary) a non linear physical model. In fact we are actually working on this kind of model. But we need to ensure that it will be possible with this non linear model to find a methodology permitting a good identification of the various parameters.