Discovering and exploring graphs: part 1

Common thread problem and rules of the game

Common thread

The first problem adressed in this course is the following:

• Where can I cycle from home using cycle paths?

For this study, we will consider the cycle paths of the Parisian region, a description of which is given on this web page:

• https://opendata.paris.fr/explore/dataset/reseau-cyclable/information

In order to perform this study, we have to answer to two intermediate questions:

1. How to model the data useful to the problem?

2. How to extract the solution of our problem from the modeling of the data?

The first question will lead us to introduce the notion of a graph while the second one will lead us to study graph search algorithms (connected component search).

Organization of the course

Every section with a title labeled “Exo” refers to exercises related to the common thread problem. You must answer these questions in groups of 4 students and record your answers in a report. For this you must

• create one google doc per group;

• share it with other group members; and

• share it at the start of the session with the teacher.

For questions that require code, you will be asked to copy the code you produced into your report. For this type of questions, you will not be asked to write an entire program on your own but to complete a graph library written in C. Thus, you should never have to produce more than twenty lines of code per question.

The report produced will be used for your evaluation in the “Graphs and Algorithms” course.

In general, each section labeled “Exo” is followed by a section labeled “Course” which presents the concepts necessary to answer the questions related to the common thread problem.

In the flow of the course sections, you will also find small quizzes which aim to test your understanding of the course. To check your answers, all you have to do is click on the “correct” button at the end of the exercise.

This course is not a mooc! A teacher is here to help you: call hime whenever you have the slightest doubt or to check your answers. The teacher can also enter comments directly in your report. Take these remarks into account to improve your answers.

A “toy example”

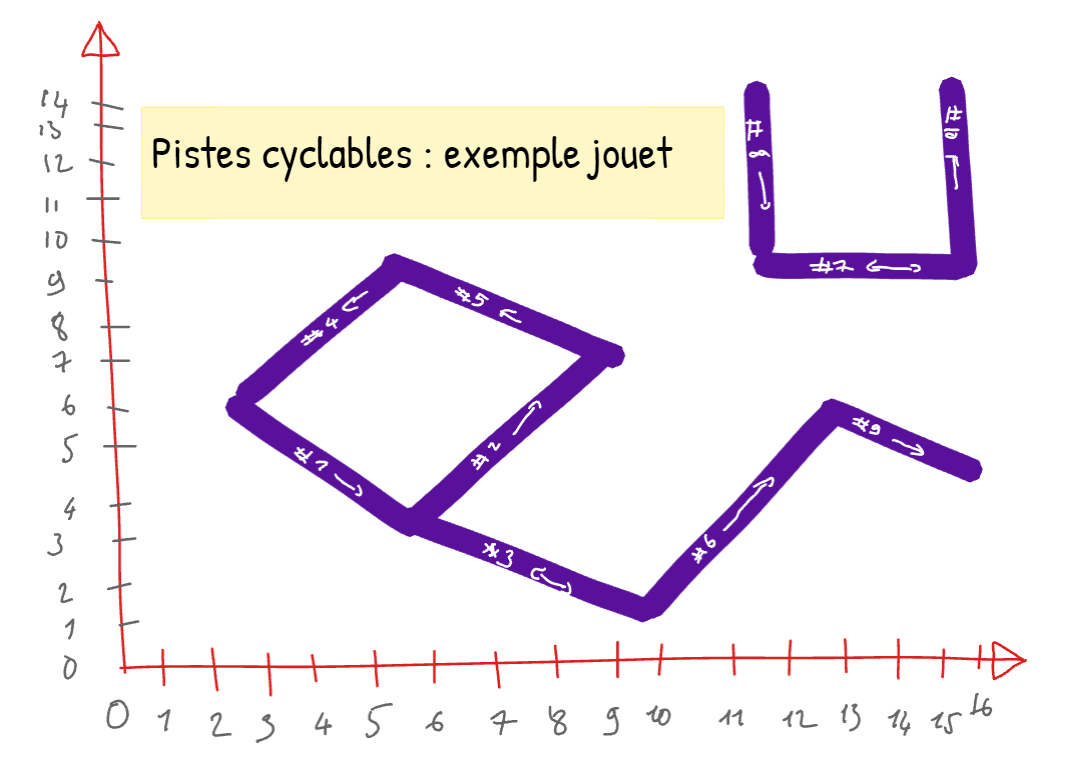
Consider the following cycle paths identified by their ends in a Cartesian coordinate system:

1. one way from (3;6) to (6;3)

2. one way from (6;3) to (9;7)

3. two-way between (6;3) and (10;1)

4. one way from (6;9) to (3;6)

5. one way from (9;7) to (6;9)

6. one way from (10;1) to (13;6)

7. two-way between (12;9) and (16;9)

8. one way from (12;13) to (12;9)

9. one way from (13;6) to (16;4)

10. one way from (16:9) to (16;13)

Exo - Modeling the data with a graph

1. Draw the graph \(G = (V,A)\) tha model the data of the “toy example” problem.

2. How many vertices does this graph have?

3. How many arcs does this graph have?

4. What do the vertices of the graph correspond to?

5. Number the vertices of the graph? From now on, we can assume that \(V = \{0, ..., n-1\}\), the integer \(n\) being the number of vertices of the graph.

6. List the arcs of \(G\).

7. For each vertex of \(G\), give the set of all its sucessors.

Course - Graph

A graph is an abstract data structure used to represent relationships between data. For example, we can represent by a graph the relations between

• criminal cases,

• courses in an engineering school,

• people on a social network,

• towns, neighborhoods, crossroads,

• the pixels of an image,

• DNA fragments, etc.

Reminder on sets

The notion of a graph is defined and studied in the mathematic framework of set theory. We start by reminding some set notations useful for the rest of our discussion.

Let \(E\) be a finite set.

A set \(S\) is called a subset of \(E\) or a part of \(E\) if every element in \(S\) is also an element in \(E\).

If \(S\) is a subset of \(E\), we write \(S \subseteq E\).

The set of all parts of \(E\) is denoted by \(\mathcal{P}(E)\)

The number of elements in a set \(E\) is denoted by \(|E|\) and we say that \(|E|\) is the cardinality of \(E\)

Let \(E = \{a,b,c\}\), indicate wether the following statements are true (V) or false (F)

1. \(\{a,b\}\) is a set.

2. \((a,b)\) is a set.

3. \((a,b)\) is a pair.

4. \(\{a,b\} = \{b,a\}\).

5. \((a,b)=(b,a)\).

6. An element can appear more than once in a set.

7. An element can appear more than once in a pair.

8. \((a,a)\) is a pair.

9. \(a\) is a subset of \(E\).

10. \(\{a\}\) is a subset of \(E\).

11. \(\{a,c\}\) is a subset of \(E\).

12. \(\{a,e\}\) is a subset of \(E\).

13. \(\emptyset\) is a subset of \(E\).

14. \(\mathcal{P}(E) = \{\{a,b\}, \{a,c\}, \{b,c\}, \{a,b,c\}\}\).

15. \(\mathcal{P}(E) = \{\{a\}, \{b\}, \{c\},\{a,b\}, \{a,c\}, \{b,c\}, \{a,b,c\}\}\).

16. \(\mathcal{P}(E) = \{\emptyset, \{a\}, \{b\}, \{c\},\{a,b\}, \{a,c\}, \{b,c\}, \{a,b,c\}\}\).

Complete with the appropriate numerical value:

1. \(|E|=\)

2. \(|\mathcal{P}(E)|=\)

3. \(|\{1,2,3,4\}|=\)

4. \(|\mathcal{P}(\{1,2,3,4\})|=\)

First definition of a graph

We will see a first definition of a graph. This definition is the most natural for representing data among which some are in (binary) relation. We will see later another equivalent representation (by successor map) which leads to a more efficient resolution of some problems formulated in terms of graph.

Definition: Graph

A graph is a pair \(G=(V,A)\) such that:

• \(V\) is a finite set; and

• \(A\) is a set of pairs of elements in \(S\)

In applications, when we model the data of a problem by a graph,

1. the set \(V\) corresponds to the data: we associate a datum to each element in \(S\); and

2. the set \(A\) allows us to encode the relation between these data: each pair of data in relation is an element of \(A\).

Definition: vertex and arc

If \(G=(V,A)\) is a graph,

• every element in \(V\) is called a vertex of \(G\); and

• every element in \(A\) is called an arc of \(G\).

Each data is therefore modeled by a vertex of the graph and each pair of related data is called an arc of the graph.

Example: Friendship graph

Consider a group of four people:

0. Jean;

1. Daniel;

2. Yukiko; and

3. Michel.

We also know that:

0. Jean likes Daniel ;

1. Daniel likes Jean ;

2. Yukiko likes Michel ; and

3. Jean likes Michel.

This information can be represented by the graph \(G = (V,A)\) such that:

• \(V = \{Jean, Daniel, Yukiko, Michel\}\); and

• \(A = \{(Jean, Daniel), (Daniel, Jean), (Yukiko, Michel), (Jean, Michel) \}\).

\(Jean, Daniel, Yukiko, Michel\) are then the vertices of \(G\) and \((Jean, Daniel), (Daniel, Jean), (Yukiko, Michel), (Jean, Michel)\) are the arcs of \(G\).

We remark that the pair \((Yukiko, Michel)\) is an arc of \(G\) but that \((Michel, Yukiko)\) does not belong to \(A\) and therefore does not form an arc of \(G\). In other words, the relation “likes” between the four people is not symetric and we say that the associated graph is not symetric. We will formally discuss this concept a little later in this ressource.

Visual representation of a graph

A graph can be visually represented by a drawing:

1. each vertex is then represented by a circle (possibly numbered to be able to find the link with the data); and

2. each arc is an arrow joining the circles representing the vertices in relation.

In the drawing, the position of the vertices is irrelevant because what interests us is the relationship between the data. It is sometimes said that we are interested in the topology of data as opposed to their geometry. In topology, a central concept is that of neighborhood. We will discuss this notion of neighborhood for graphs in the next section.

Example: Drawing of the friendship graph

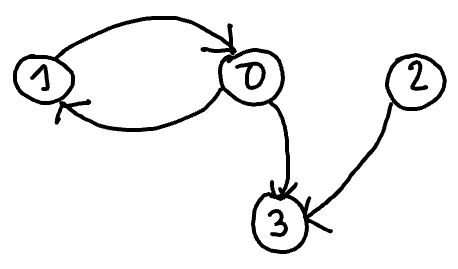
We can represent the graph \(G =(V,A)\) seen in the previous section by the following drawing:

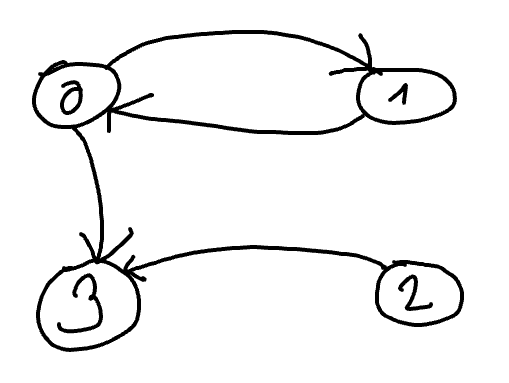
In the drawing, the number of the vertices makes it possible to find the link with the people put in contact. We recall (and we use in the drawing above) the following numbering:

0. Jean;

1. Daniel;

2. Yukiko; and

3. Michel.

As the position of the vertices does not matter, we can also very well draw the following for \(G\).

Successor map (neighborhood)

We will see in this section that a graph can be defined in an equivalent way using the notion of neighborhood. This alternative definition is very useful in practice since it allows one to browse or traverse the data step by step. Intuitively, given (a graph representing) data in pairwise relation, the neighborhood of one of these data is made up of all the data in relation with it.

Definition: successor and predecessor

If \(G=(V,A)\) is a graph and if \((a,b)\) is an arc of this graph, we say that

• \(b\) is a successor of \(a\); and that

• \(a\) is a predecessor of \(b\).

Example: Successors and predecessors in the friendship graph

In the graph \(G =(S,A)\) of the previous example:

• \(Michel\) is a successor of \(Jean\) and \(Jean\) is a predecessor of \(Michel\) since the set \(A\) contains the arc \((Jean,Michel)\); but

• \(Jean\) is not a successor of \(Michel\) since the pair \((Michel,Jean)\) is not an arc of \(G\) (that is to say \((Michel,Jean)\) does not belong to \(A\)).

We also note that a vertex can be both the predecessor and the successor of another. For example, \(Jean\) is both a predecessor and a successor of \(Daniel\).

We can also observe that \(Michel\) has no successor and that \(Yukiko\) has no predecessor.

We note that in this graph no vertex is a successor of itself. However, in general, it is quite possible that a vertex \(x\) be its own successor (and its own predecessor) if the pair \((x,x)\) is an arc. Such an arc from a vertex to itself is ofte called a loop.

Definition: Sucessor map

Let \(G = (S,A)\) be a graph, the successor map of \(G\), denoted by \(\Gamma_G\), is the map which associates to any vertex of \(G\) the set of its sucessors, namely :

\begin{eqnarray} \Gamma_G :~& S &\longrightarrow & \mathcal{P}(S)\\ & a & \longmapsto & \Gamma_G(a) = \{b~;~(a,b) \in A\}. \end{eqnarray}

Given a graph \(G\) and one of its vertices \(x\), the set \(\Gamma_G(x)\) is sometimes called the “neighborhood” ofe \(x\) (in the graph \(G\)).

Given the grap \(G = (S,A)\) from the previous examples (“friendship graph”) and given its application map \(\Gamma_G\), indicate whether the following statements are true (V) or false (F).

1. \(Yukiko\) is a successor of \(Michel\).

2. \(Yukiko\) is a predecessor of \(Michel\).

3. \(Michel \in \Gamma_G(Yukiko)\).

4. \(Yukiko \in \Gamma_G(Michel)\).

5. \(\Gamma_G(Jean) = \{Daniel, Michel\}\).

6. \(\Gamma_G(Daniel) = Jean\).

7. \(\Gamma_G(Daniel) = \{Jean\}\).

8. \(\Gamma_G(Michel) = \{\emptyset\}\).

9. \(\Gamma_G(Michel) = \emptyset\).

10. \(\Gamma(Yukiko) = \{Michel\}\).

As seen with items 5-10 of the previous exercise, knowing the set of vertices of a graph and its set of arcs, we can always deduce its successor map. This is a direct consequence of the definition of the successor map. We will see that, conversely, if we know the set of vertices of a graph \(G\)Gamma_G`, then, it is possible to deduce the set of arcs of this graph. In other words, the set of arcs of the graph conveys exactly the same information as the successor map: the two representations (by set of arcs and by successor map) are therefore equivalent.

We will start by convincing ourselves on an example that it is possible to deduce the set of arcs of a graph from its successor map, then we will state the mathematical property which precisely establishes the equivalence between the two representations of graphs .

Let \(G\) be the graph

• whose vertex set if \(V = \{0, 1, 2, 3 \}\) ; and

• whose successor map \(\Gamma_G\) is defined by

  • \(\Gamma_G(0) = \{0,1,2\}\)

  • \(\Gamma_G(1) = \{1\}\)

  • \(\Gamma_G(2) = \{0, 1\}\)

  • \(\Gamma_G(3) = \emptyset\).

Indicate, for each of the following statement, whether it is true (V) or false (F).

1. \((0,0)\) is an arc of \(G\).

2. \((0,1)\) is an arc of \(G\).

3. \((0,2)\) is an arc of \(G\).

4. \((0,3)\) is an arc of \(G\).

5. \((1,0)\) is an arc of \(G\).

6. \((1,1)\) is an arc of \(G\).

7. \((1,2)\) is an arc of \(G\).

8. \((1,3)\) is an arc of \(G\).

9. \((2,0)\) is an arc of \(G\).

10. \((2,1)\) is an arc of \(G\).

11. \((2,2)\) is an arc of \(G\).

12. \((2,3)\) is an arc of \(G\).

13. \((3,0)\) is an arc of \(G\).

14. \((3,1)\) is an arc of \(G\).

15. \((3,2)\) is an arc of \(G\).

16. \((3,3)\) is an arc of \(G\).

17. \(G = (V,A)\) with \(A= \{(0,1), (0,2), (2,0), (2,1)\}\).

18. \(G = (V,A)\) with \(A= \{(0,0), (1,0), (2,0), (1,1), (0,2), (1,2)\}\).

19. \(G = (V,A)\) with \(A= \{(0,0), (0,1), (0,2), (1,1), (2,0), (2,1)\}\).

Property: Graph representations

Let \(G\) be a graph whose vertex set is \(V\), whose arc set is \(A\), and whose successor map is \(\Gamma_G\). The following statement is true:

• for any two elements \(x\) and \(y\) in \(V\), the pair \((x,y)\) is an element of \(A\) if and only if \(y\) is an element of \(\Gamma_G(x)\).

The previous property establishes that we can represent a graph by the pair \((V,A)\) or by the pair \((V, \Gamma_G)\). Therfore, the pair \((V, \Gamma_G)\) is also called a graph. Depending on our needs, we can now consider either of these representations indifferently.

Exo - Memory representation of a graph

1. Draw the memory representation of the graph modeling the data of the “toy example” problem

   • if we use an array of linked lists

   • if we use a Boolean matrix

   • if we use an aray of arcs (arrays head and tail)

2. In the “toy example” graph, what complementary information can we benefit from having associated with the vertices of the graph? Represent the array (or arrays) used to store this additional information

3. A C code to represent a graph has been implemented for you. Read the file graphes.h and indicate how the graphs are stired in this code.

Cours - Memory representation of a graph

We will study three fundamental memory representations for graphs:

• by array of linked lists

• by Boolean matrix (that is to say bay aray of Boolean arrays)

• by array of arcs

The first two aim at representing the successor map of the graph in memory, while the third one is intended at the representation of set the arcs of the graph. Whatever representation you choose, vertices are always represented the same way. As we saw previously, the successors of a vertex form a subset of the vertices of the graph. We therefore also study how to represent a subset of vertices in memory. The outline of this chapter is therefore as follows.

1. Memory representation for the vertices of a graph

2. Memory representation of a subset of vertices: linked list and Boolean array

3. Memory representation of a graph using an array of linked lists

4. Memory representation of a graph by boolean matrix

5. Memory representation of a graph by array of arcs

Memory representation for the vertices of a graph

In the memory of a computer, the set of vertices of a graph:math:G, with \(n\) vertices, is represented by:

• a set of consecutive integers starting at the value 0 and ending at the index \(n-1\). Thus, we set in the remaining art of the course \(S = \{0, \ldots, n-1\}\). In memory, it is sufficient to store the number \(n\) of vertices of the graph and we therefore do not explicitly store the complete list of integers from 0 to \(n-1\); and

• possibly, one (or more) table to associate additional information to each vertex. The information related to the vertex i is stored at index i of this table.

Example: memory representation of the vertices of the friendship graph

The friendship graph presented in the previous section has 4 vertices associated with the names of the four friends. So in memory,

• the vertices of the graph will be the integers 0, 1, 2, 3 and we just have to remember that the graph contains 4 vertices;

• we consider an additional array, called info, such that info[0] = "Jean", info[1] = "Daniel", info[2] = "Michel" and info[3] = "Yukiko". This table memorizes the association between the numbers of the vertices and the first names of the four friends.

Memory representation of a subset of vertices: linked list and Boolean array

In the remainder of this section, we denote by \(X\) the subset of \(V = \{0, \ldots, n-1\}\) that we want to represent in memory.

The set \(X\) can be represented by a linked list.

• The linked list is made up of nodes.

• Each node respresents an element of \(X\).

• Each node is made of two fields:

  • the first one is an element of \(S\) (thus, an integer between \(0\) and \(n-1\) );

  • the second one is a pointer to the next link in the linked list; the NULL pointer indicating the end of the list.

• The list is referenced by the address of its first link or by the NULL pointer if the set \(X\) is empty.

Example: memory representation of a subset by a linked list

The subset \(X = \{1,2,4\}\) of \(V = \{0, \ldots, 9\}\) can be represented by the linked list drawn below:

The set \(X\) can also be represented by a Boolean array.

• The Boolean array is made of \(n\) positions, indexed from \(0\) to \(n-1\).

• The value at index \(i\) is equal to true if \(i\) is an element of \(X\).

• The value at index \(i\) is equal false is \(i\) is not an element if \(X\).

Example: representation of a subset by a Boolean array

The subset \(X = \{1,2,4\}\) of \(S = \{0, \ldots, 9\}\) can be represented by the following array:

The efficiency of graph algorithms very often depends on elementary operations performed on sets (subset of vertices, set of successors, etc.). The choices of the data structures to represent these sets must therefore be made with care, taking into account the efficiency of the involved elementary operations. In the following exercise, you are asked to evaluate the algorithmic complexity of the elementary set operations according to whether we choose to implement a set by a linked list or by a Boolean array. In order to be able to subsequently design efficient graph algorithms, it is therefore necessary to be able to quickly find the answers to the following exercises on your own.

Give the time complexity of each of the operations below, depending on whether the subset \(X\) de \(S = \{0, \ldots, n-1\}\) is implemented with a linked list (LL)or with a Boolean arraey (BA).

Opération	peudo-code	CComplexity L	Complexity BA
Initialization	\(X := \emptyset\)	O()	O()
Test if empty	if (\(X = \emptyset\))	O()	O()
Selection	\(x :=\) any element in \(X\)	O()	O()
Selection-deletion	\(x :=\); \(X := X \setminus \{x\}\) ;	O()	O()
Search	if (\(x \in S\))	O()	O()
External insertion 1	\(X := X \cup \{x\}\)	O()	O()
General insertion 2	\(X := X \cup \{x\}\)	O()	O()
Deletion	\(X := X \setminus \{x\}\)	O()	O()
Traversal	For each \(x\) in \(X\)	O()	O()

Notes

1

An insertion of an element \(x\) in a set \(X\) is said to be external when it is known in advance that the element \(x\) to be inserted doeas not belong to \(X\).

2

An insertion of an element \(x\) in a set \(X\) eis said to be general when it is not known in advance whether the element \(x\) to be inserted already belongs to the set \(X\).

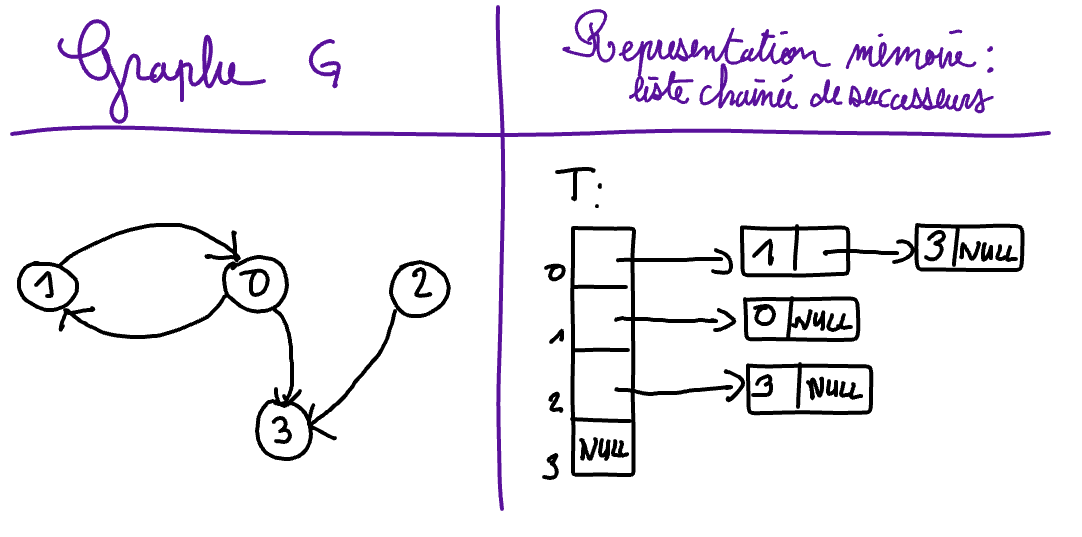
Memory representation of a graph using an array of linked lists

With this first memory representation of graphs, we must store the two following pieces of information:

• the vertex set of \(G\) being the set \(V = \{0, \ldots, n-1\}\), it is sufficient to save the number \(n\) of vertices in order to store the vertices of the graph;

• the successor map of \(G\) is stored in memory with an array T of linked list such that:

  • T[i] points towards an linked list representing the set \(\Gamma_G(i)\) of the successors of the vertex \(i\).

Example

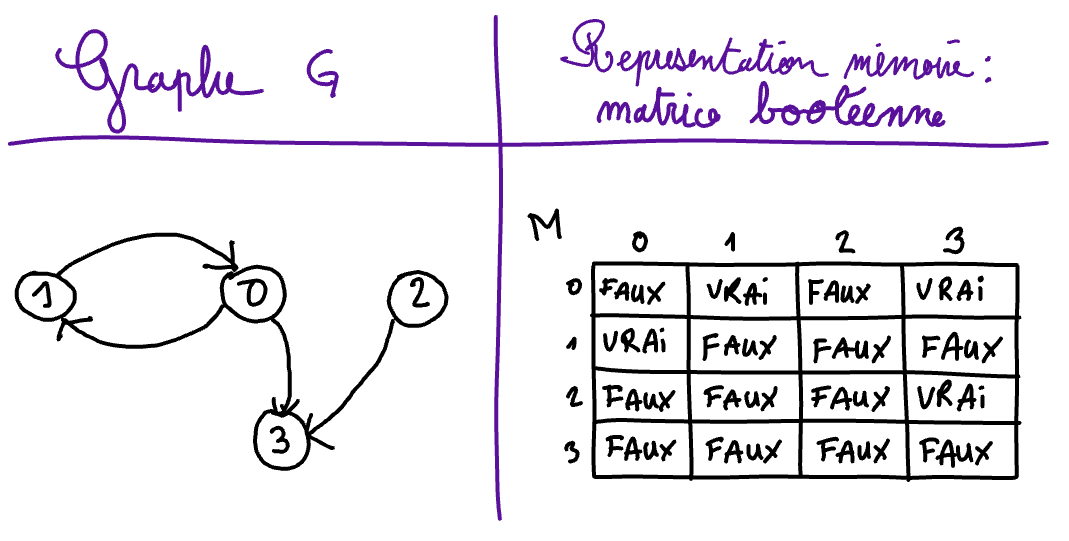
Memory reresentation of a graph by Boolean matrix

As before, with this second memory representation of graphs, we must store two pieces of information:

• the vertex set of \(G\) being the set \(V = \{0, \ldots, n-1\}\), it is sufficient to save the number \(n\) of vertices in order to store the vertices of the graph;

• the sucessor map of \(G\) is stored with a Bolean matric M of size n by n (n rows, each of which with n elemnts):

  • The row i is the representation of the set \(\Gamma(i)\) of the sucessors of vertex \(i\) with a Boolean array. In other words, we have T[i][j] = TRUE if and only if vertex \(j\) is a succssor of vertex \(i\).

Example

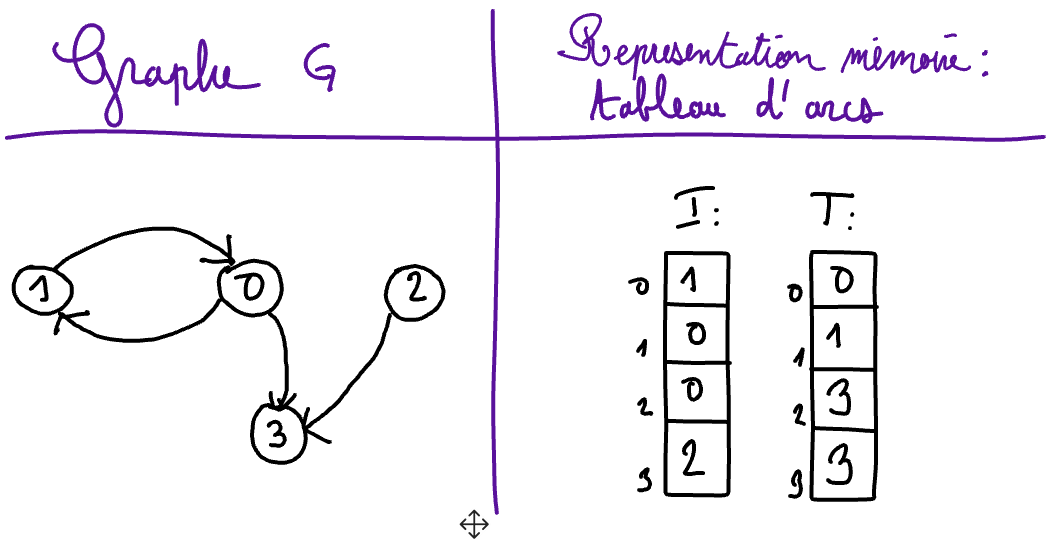
Memory reresentation of a graph by an array of arcs

Finally, with this third memory representation of graphs, it is necessary to store the following three pieces of information:

• the vertex set of \(G\) being the set \(V = \{0, \ldots, n-1\}\), it is sufficient to save the number \(n\) of vertices in order to store the vertices of the graph;

• The number \(m\) of arcs of the graph is also stored.

• The arcs of the graph are arbitrarily numbered and they are represented by two arrays I and T of \(m\) integers such that

  • I[i] is the initial vertex f the arc numbered \(i\) ; et

  • T[i] i_s the terminal vertex of the arc numbered \(i\).

Example

Exo - One way graphs

You may have experienced it yourself, some cyclists in Paris are “rebels”! They happily use the cycle paths in the forbidden direction. We can however distinguish two categories of rebels:

1. the rebel-rebel only takes the wrong way cycle paths; ;

2. the practical-rebel takes the cycle path indifferently in the correct or in the prohibited direction, depending on what is the most practical for him.

Given a graph \(G = (V,A)\) found in the previous common-thread exercises ,

• What graph should we consider to model the journey of rebel-rebel people?

• What graph should we consider to model the journey of practical-rebel people?

Name these two graphs by using graph theory vocabulary and draw them (in the case of the toy example).

If, for a given city, the graph of the cycle paths is symetric, what can we conclude about the cycle paths of this city?

Course - Symmetric and graphs

In this section we study the notions of

• symmetric of a graph,

• symmetric closure of a graph; and

• symmetric graph.

This will lead us, in a next section, to introduce our first graph algorithm whose objective will be precisely to compute the symmetric of a given graph.

Definition: symmetric of a graph

Let \(G = (V,A)\) be a graph. The symetric of \(G\) is the graph, denoted by \(G^{-1}\), such that:

• the set of vertices if \(G^{-1}\) is equal to the set of vertices of \(G\); and

• for each vertex \(x\) in \(G^{-1}\), we have \(\Gamma_{G^{-1}}(x) = \{ y \in S \text{ such that } x \in \Gamma_G(y) \}\).

In other words,

• \(G\) and \(G^{-1}\) have the same vertices; and

• a vertex \(y\) is a successor of a vertex \(x\) in \(G^{-1}\) if and only if \(x\) is a successor of \(y\) in \(G\).

Thus, we can observe that \((x,y)\) is an arc of \(G^{-1}\) if and only if \((y,x)\) is an arc of \(G\). Graphically, it is sufficient to “reverse the arrows” of the graph \(G\) to obtain those of \(G^{-1}\).

Example

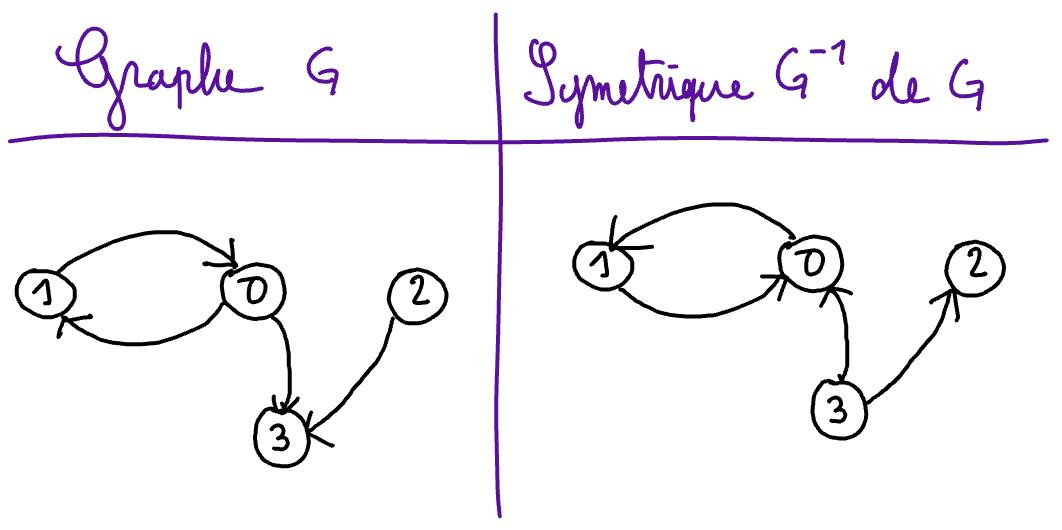
In the following example, we have:

• \(G = (\{0,1,2,3\}, \{ (0,1), (1,0), (0,3), (2,3)\})\) et

• \(G^{-1} = (\{0,1,2,3\}, \{ (1,0), (0,1), (3,0), (3,2)\})\).

As the graph \(G\) above represents the relation “likes” in the group of 4 friends (cf first example of the course), we may affirm that the graph \(G^{-1}\) rpresents the relation “is liked by” in this same group.

Definition: symmetric graph

Let \(G = (S,A)\) be a graph. We say that \(G\) is a symmetric graph if it is equal to its symmetrcic, that is, if

• \(G^{-1} = G\).

Consider the 3 gfollowing graphs and answer true (V) or false (F) :

• \(G_1 = (S_1, A_1)\) with \(S_1 = \{0, 1, 2\}\) and \(A_1 = \{(0,0), (0,1), (1,0)\}\) ;

• \(G_2 = (S_2, \Gamma_{G_2})\) with \(S_2 = \{0, 1, 2\}\) and \(\Gamma_{G_2}(0) = \{1,2\}, \Gamma_{G_2}(1) = \{2\},\) and \(\Gamma_{G_2}(2) = \emptyset\) ;

• \(G_3\) is the graph drawn below.

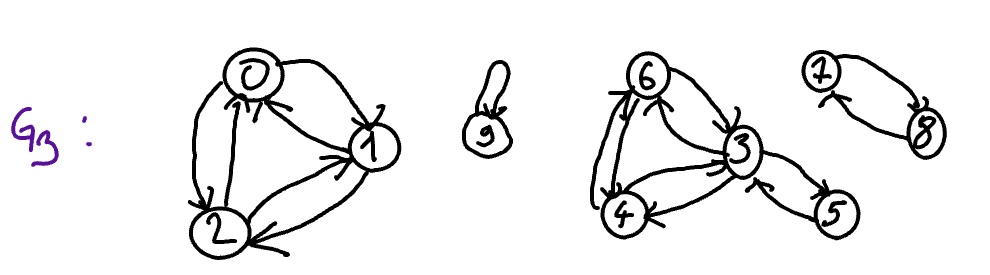
Indicate for each statement below if it is true (V) or false (F).

1. \(G_1\) is symmetric.

2. \(G_2\) is symmetric.

3. \(G_3\) is symmetric.

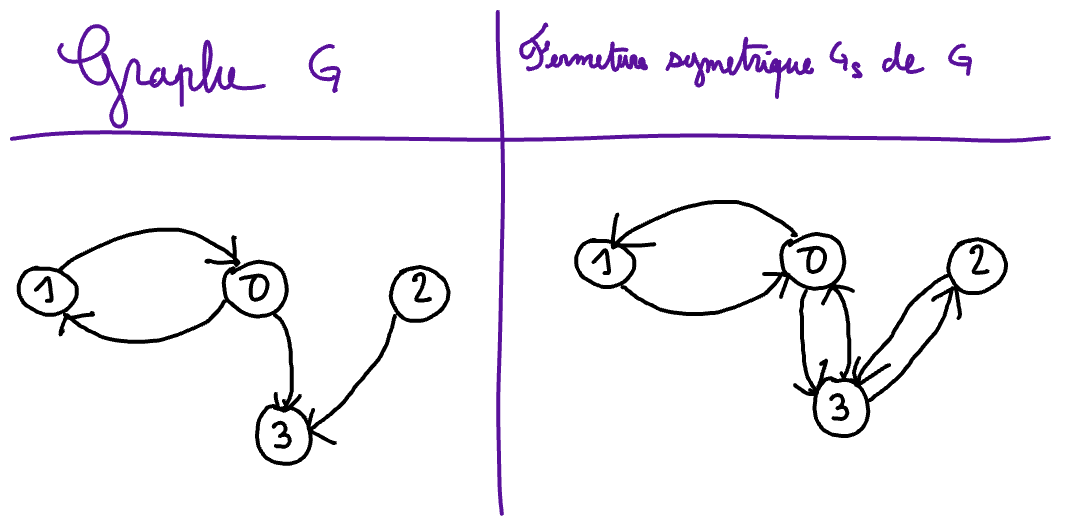
Définition: Symetric closure

Let \(G\) be a graph. The symetric closure of \(G\) is the graph, denoted by \(G_s\), such that

• the set of vertices of \(G_s\) is equal to the set of verices of \(G\) ; and

• the set of arcs of \(G_s\) is equal to the union of the sets of arcs of \(G\) and of its symetric \(G^{-1}\).

Exemple

Exo - Implementing a first graph algorithm

We have made for you the following code to compute the symmetric of a graph using the library graphes.h studied previously.

#include "graphes.h"

graphe * symInefficace(graphe * g)
/* ====================================================================== */
{
    graphe *g_1;
    int nsom, narc, k, x, y;
    pcell p;

    nsom = g->nsom;
    narc = g->narc;
    g_1 = initGraphe(nsom, narc); /* Initialise une structure pour un graphe de nsom sommets et narc arcs */

    for (y = 0; y < nsom; y++) /* pour tout y sommet de g */
        for (x = 0; x < nsom; x++) /* pour tout x sommet de g */
            if (estSuccesseur(g, x, y)) /* si y est un successeur de x dans g */
                ajouteSuccesseur(g_1, y, x); /*  gamma_1[y] =: gamma_1[y] U {x} */
    return g_1;
} /* Sym() */

This code uses function estSuccesseur givent below:

int estSuccesseur(graphe *g, int x, int y)
/* ====================================================================== */
{
    pcell p; /* pointeur de maillon utilise pour parcourir la liste de successeurs */
    int z; /* pour stocker les successeurs de x */
    /* parours de la liste des successeurs de x */
    p = g->gamma[x];
    while(p != NULL){
        z = p->som;
        if (z == y) return 1;
        p = p->suivant;
    }
    /* On a atteint la fin de la liste des successeurs sans trouver y */
    return 0;
} /* EstSuccesseur() */

The underlying algorithm is not efficient. Assess its time complexity as a function of the number \(n\) of vertices of the graph and of the number \(m\) of arcs. Justify with few arguments given in natural language (no need for any mathematical formalization here).

Give the implementation in C of a linear time algorithm ( \(O(n+m)\) ) to compute the symmetric of a graph. To this end, complete the following source code which was started for you.

graphe * symEfficace(graphe * g)
/* ====================================================================== */
{
    graphe *g_1;
    int nsom, narc, k, x, y;
    pcell p;

    nsom = g->nsom;
    narc = g->narc;
    g_1 = initGraphe(nsom, narc);
    /* A Completer ci-dessous, possible en 3 lignes, souhaitable en moins de 6 :-) */

    return g_1;
} /* Sym() */

In order to test these two algorithms in practice, we provide you with the following files that you must downoad:

• graphes.h contains the prototype of the graph structure and the prototype of the elementary functions to handle graphs.

• graphes.c contains the codes of the elementary functions to handle graphs which were prototyped in graphes.h

• symetrique.c contains the codes given above, as well as a main function that

  1. reads a graph from a file whose acess path is given as a parameter to the program;

  2. compute the symmetric of this graph (by using the inefficient function). Observe that the execution time is measured and displayed on the screen; and

  3. save the result in a file whose acess path is given as a second argument to the program.

In order to use this program to compute the symmetric of a graph under Linux you must:

1. download the files above and save them in a single directory

2. open a terminal et set the working directory to the directory containing your source files

3. compile the programm with the command gcc graphes.c symetrique.c -o symetrique` (even better by using make and this Makefile thas can be downloaded)

4. execute the program with the command ./symetrique entree.graphe resultat.graphe

Verify the result of these two algorithms 3 on a graph of small size (for instance on amitie.graphe). In order to verify that the resilt is correct, it is sufficient to edit with a text editor the file containing the input graph and to compare it with the one containing the resulting graph produced by the program.

Report the execution times 3 of the two algorithms for several graphs:

• random graph with 100 vertices and 500 arcs

• random graph with 1 000 vertices and 5 000 arcs

• random graph with 10 000 vertices and 50 000 arcs

• random graph with 100 000 vertices and 500 000arcs

• random graph with 10 000 vertices and 20 000 arcs

• random graph with 10 000 vertices and 150 000 arcs

• random graph with 10 000 vertices and 200 000 arcs

• random graph with 10 000 vertices and 300 000 arcs

• subset of the cyces paths 4

• cycle paths (complete)

Comment the computation time results. Is it consistent with the time complexity of the studied algorithms?

Notes

3(1,2)

Do not forget ton insert in symetrique.c the code that you have produced for the function symEfficace, and to call this function from the main program when you want to measure the execution times of the efficient algorithm to compute the symmetric of a graph!!

4

Bonus: Obtain a graph visualization! To this end

• download the source file graphe2ps and save it in your directory

• compile it, for instance, with the command gcc graphe2ps.c graphes.c -o graphe2ps -lm

• This program allows you to convert a graph in the form of a file .graphe into a graphical illustration in the form of a .eps file that can be visualized for instance a pdf viewer as evince.

Do not forget to include a visulaization of (some) of your graphs in your report ;-) !

Course - SYM Algorithm: computing the symmetric of a graph

In this section, we are interested in the following porblem:

• given a graph \(G\),

• compute the symmetric of \(G\).

In the case where we represent the graphs by arrays of arcs, a trivial algorithm to solve this problem (in constant time) consists in swapping the two arrays “I” and “T”.

We propose below an algorithm for the case of graphs represented by their successor map and we analyze its complexity in the following two cases:

We propose below an algorithm for the case of graphs represented by their successor map and we analyze its complexity in the following two cases:

• successor maps are stored as Boolean matrices; and

• successor maps are stored as aray of linked lists.

Algorithm SYM

• Data: the number \(n\) of vertices in the graph \(G\) and the successor map \(\Gamma\) of the graph \(G\)

• Result : the sucessor map \(\Gamma^{-1}\) of the symmetric of \(G\)

1. For each \(x\) from \(0\) to \(n-1\) Do \(\Gamma^{-1}(x) := \emptyset\)

2. For each \(x\) from \(0\) to \(n-1\) Do

   3. For each \(y\) in \(\Gamma(x)\) D

      4. \(\Gamma^{-1}(y) := \Gamma^{-1}(y) \cup \{x\}\)

To analyze the time complexity of an algorithm, it is necessary to analyze the time complexity of each of its lines.

Let us first assume that \(\Gamma\) and \(\Gamma^{-1}\) are represented by Boolean matrices and let us denote by \(m\) the number of arcs of the graph \(G\).

1. The complexity of Line 1 is \(\mathcal{O}(n^2)\) since this line consists of initializing \(n\) subsets stored as Boolean arrays.

2. The complexity of Line 2 is trivialy \(\mathcal{O}(n)\).

3. The complexity of Line 3 is \(\mathcal{O}(n^2)\) since this line consists of traversing \(n\) subsets stored as Boolean matrices.

4. The complexity of Line 4 is \(\mathcal{O}(m)\) since this line is executed exactly once for each arc of the graphe and, for each arc, it consists of inserting an element in a subset represented as a Boolean array.

As \(m\) is less than \(n^2\), we deduce the following property which established the time complexity of SYM algorithm in this first case.

Complexity of SYM algorithm with Boolean matrices

When the graphs are stored in the form of Boolean matrices, the time complexity of SYM algorithm is

• \(\mathcal{O}(n^2)\),

where \(n\) is the number of vertices in the given graph \(G\).

Let us now assume that \(\Gamma\) and \(\Gamma^{-1}\) are represented by arrays of linked lists.

1. The complexity of Line 1 is \(\mathcal{O}(n)\) since this line consists of initializing \(n\) subsets stored as linked lists.

2. The complexity of Line 2 is trivialy \(\mathcal{O}(n)\).

3. The complexity analysis of Line 3 is more tricky. Lin 3 consists of browsing the list of sucessors of ecery vertex of the graph. The algorithm to L’algorithme de traverse a linked list L is the following:

   n := L.firstNode
   While (n != NULL) Do
       x := n.vertex // x takes the value of the vertex associated to the node n (first field of n)
       // instructions to be performed on vertex  x
       n := n.next // n takes the value of the adress of the next node  (second field of n)
   

We observe that to browse a list of \(k\) elements, Line 1 is executed once, the test at Line 2 is executed \(k+1\) times (\(k\) positive tests followed by one negative test), and the instructions of Lines 3-5 are executed \(k\) times. In SYM Algorithm, at Line 3, \(n\) list traversals are performed and the total number of elements contained in these lists is \(m\) (since the graph is made of \(m\) arcs). Thus, the time complexity of Line 3 in SYM algorithm is \(\mathcal{O}(n+m)\).

4. The complexity of Line 4 is \(\mathcal{O}(m)\) since this line is executed exactky \(m\) times and since it consists of inserting an external element in a list (constant time operation).

Time complexity of SYM algorithm with linked lists of successors

When the graphs are stored in the form of arrays of linked lists, the time complexity of SYM Algorithm is

• \(\mathcal{O}(n+m)\),

wher \(n\) and \(m\) are the numbers of vertices and of arcs, respectively, of a given graph \(G\).

When the number of arcs is not too large compared to the number of vertices, the algorithm using linked lists has better complexity than that using Boolean matrices. This advantage is reduced when the number of arcs increases and when we approach the limit case wherem=n2. This observation is very often verified for graph algorithms: it is generally advantageous to consider representation by lists of successors when the graphs to be processed are not very dense.

When the number of arcs is not too large compared to the number of vertices, the algorithm using linked lists has a better complexity than the one using Boolean matrices. This advantage is reduced when the number of arcs increases and when we tend to the limit case where \(m = n^2\). This observation is very often verified for graph algorithms: it is generally advantageous to consider the representation by lists of successors when the graphs to be processed are not very dense.

General Knowledge Bonus - Some remarkable graphs

• A graph \(G = (V,A)\) est symmetric if, for any \((a,b)\) in \(A\), the “reverse” pair \((b,a)\) is also an arc in \(A\).

• A graph \(G = (V,A)\) is asymmetric if, for any \((a,b)\) in \(A\), the “reverse” pair \((b,a)\).

• A symmetric graph is also sometimes called non-directed. A pair of arcs \(\{(a,b), (b,a)\}\) in such a graph is called an edge and can be simply represented by the set \(\{a,b\}\) for which the order of appeaeance between \(a\) and \(b\) does not matter. Graphically, we can draw an edge by a line without arrow connecting two vertices. Consequently, an undirected graph is often defined as the data of a pair \((V,E)\), where \(V\) is a finite set and where \(A\) is a set of sets of two distinct elements of S.

• A graph \(G = (V,A)\) is reflexive if , for any vertex \(x\) in \(V\), the pair \((x,x)\) is an arc in \(A\). Any arc \((x,x)\) in \(A\) is called a loop of \(G = (S,A)\).

• A graph \(G = (V,A)\) is irreflexive there is no loop for \(G\).

• A graph \(G = (V,A)\) is complete if any pair of two distinct vertices form an arc in \(A\).

Consider the graphs \(G_1, G_2, \ldots, G_5\) below.

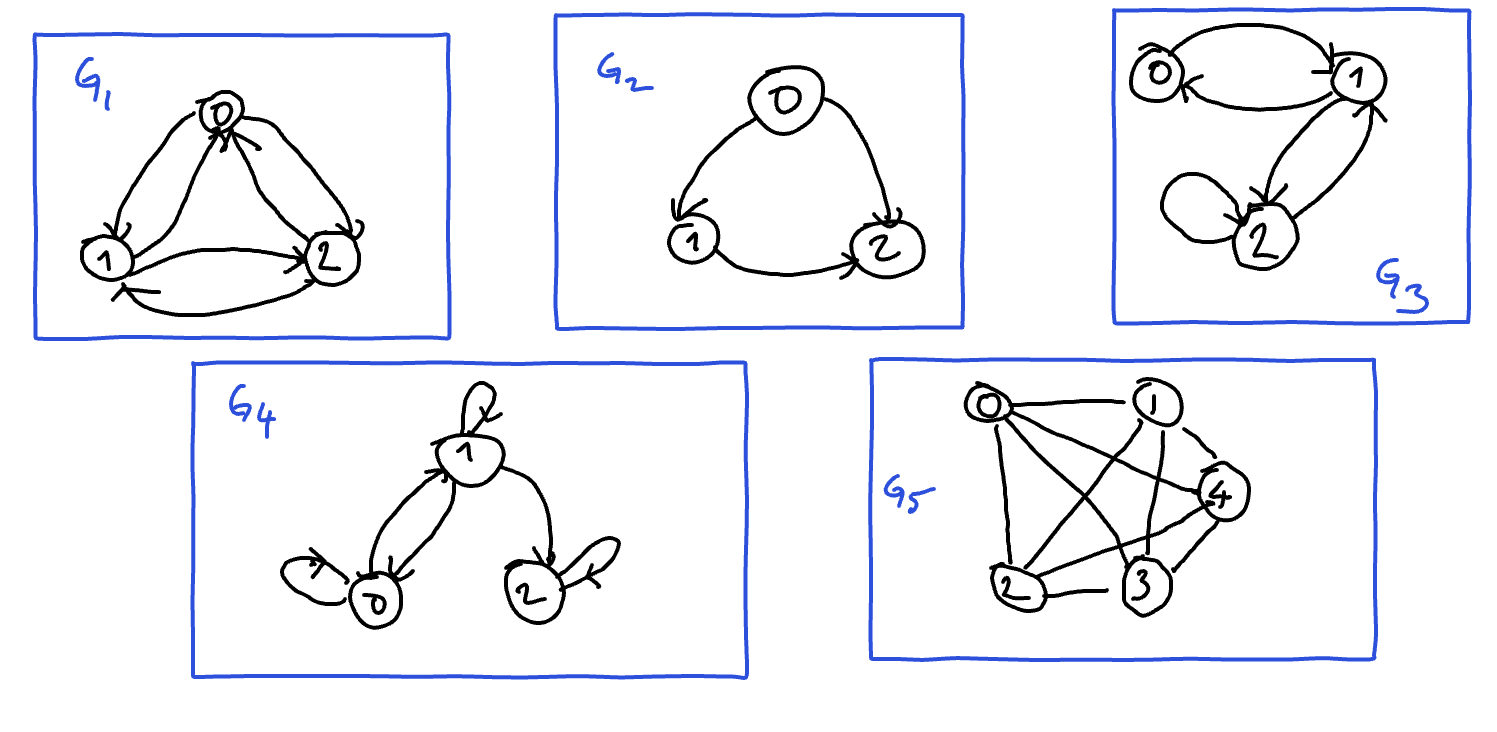
Complete below for the statement to hold true!

1. I am symmetric but not complete. I am graph numbered .

2. I am asymmetric. I am graph numbered .

3. I am made of three vertices and I am complete. I am graph numbered .

4. I am neither symmetric nor asymmetric. I am graph numbered .

5. I am complete and I have not been cited in the previous statement. I am graph numbered .

6. I am neither reflexive, nor ir irreflexive. I am graph numbered .

7. I am reflexive. I am graph numbered .