Building and optimizing a spy network - part 1: arborescence¶

Common thread problem and rules of the game¶

Common thread¶

The secret services must establish a spy network. More precisely, they have to establish a routing plan for secret messages such that a given spy can send information to a group of \(N\) other spies. Among this group of spies, some have the possibility of contacting each other and directly exchanging information while others cannot. When two spies exchange a message, the message can be intercepted with some known probability. In this course, we will answer the following questions:

How a message can be sent to all the members of the network?

How to carry out these communications while minimizing the probability that the message be intercepted?

In order to carry out this study, we will answer the following questions:

How should we model the data of the problem?

How can we select an optimal solution, (that is to say for which the probability of interception is minimal) among all possible solutions?

In order to answer these questions,

we will introduce the notion of an (edge-)weighted graph;

we will present the notions of a tree and of an arborescence; and

we will consider the problem of finding a minimum spanning tree and we will study Kruskal algorithm to solve it.

Organization of the course¶

Every section with a title labeled “Exo” refers to exercises related to the common thread problem. You must answer all these questions in groups of 4 students and record your answers in a report. You must keep the same group as for the first part of the course. You have to

continue with the google document created previously;

share it with other group members; and

share it at the start of the session with the teacher.

For questions that require code, you will be asked to copy the code you produced into your report. For this type of questions, you will not be asked to write an entire program on your own but to complete a graph library written in C. Thus, you should never have to produce more than twenty lines of code per question.

The produced report will be used for your evaluation in the “Graphs and Algorithms” course.

In general, each section labeled “Exo” is followed by a section labeled “Course” which presents the concepts necessary to answer the questions related to the common thread problem.

In the flow of the course sections, you will also find small quizzes which aim to test your understanding of the course. To check your answers, all you have to do is click on the “correct” button at the end of the exercise.

This course is not a mooc! A teacher is here to help you: call him whenever you have the slightest doubt or to check your answers. The teacher can also enter comments directly in your report. Take these remarks into account to improve your answers.

A “toy example”¶

Let us consider 9 spy-agents numbered from (00)0 to (00)9, the spy 007 must send a message to the other nine. To this end, the following communication exchanges are possible:

between spies 0 and 9 with an interception probability of 0.3%

between spies 0 and 3 with an interception probability of 0.6%

between spies 0 and 2 with an interception probability of 0.2%

between spies 1 and 3 with an interception probability of 0.3%

between spies 1 and 4 with an interception probability of 0.4%

between spies 1 and 6 with an interception probability of 0.3%

between spies 1 and 9 with an interception probability of 0.4%

between spies 2 and 5 with an interception probability of 0.6%

between spies 2 and 7 with an interception probability of 0.5%

between spies 3 and 7 with an interception probability of 0.2%

between spies 4 and 6 with an interception probability of 0.2%

between spies 4 and 8 with an interception probability of 0.4%

between spies 5 and 7 with an interception probability of 0.1%

between spies 5 and 8 with an interception probability of 0.2%

Exo - Modeling the data with a graph¶

Draw the graph that model the data of the “toy example” problem?
What do the vertices of the graph correspond to?
Explain why a non-directed graph is sufficient and what does the edges of this graph correspond to??
How would you weight the edges of this graph?

Course - Edge-weighted graph¶

In this section, we recall the definition of a non-directed graph and we introduce the notion of a weighted (non-directed) graph.

A non-directed graph is a more compact representation of a symmetric graph (without loop). In a symmetric graph, the arcs are paired since each arc \((x,y)\) can be grouped with its reversed arc \((y,x)\). In a non-directed graph, to avoid representing the two paired arcs \((x,y)\) and \((y,x)\), we only consider the unordered pair \(\{x,y\}\).

Definition: Non-directed graph

A non-directed graph is a pair \(G = (V,E)\) such that:

\(V\) is a finite set; and

\(E\) is a set of sets made of two distinc elements in \(V\).

Example

Let

\(V = \{0,1,2,3\}\); and

\(E = \{\{0, 1\}, \{1, 3\}, \{0, 2\}, \{1,2\} \}\).

The pair \(G = (V,E)\) is a non-directed graph.

Definition: Non-directed graph

Let \(G = (V,E)\) be a non-directed graph.

Each element of \(V\) is called a vertex of \(G\).

Each element of \(E\) is called an edge of \(G\).

We say that \(x\) is adjacent to \(y\) if \(\{x,y\}\) is an edge of \(G\).

If \(G = (V,E)\) is a non-directed graph, the successor map of \(G\), denoted by \(\Gamma_G\) maps to every vertex the set of vertices that are adjacent to it, that is:

\begin{eqnarray} \Gamma_G :~& V &\longrightarrow & \mathcal{P}(V)\\ & x & \longmapsto & \Gamma_G(x) = \{y~;~\{x,y\} \in E\}. \end{eqnarray}

Remark.

If \(G = (V,E)\) is a non-directed graph, the pair \((V,\Gamma_G)\) is a symmetric graph without loop, called the directed graph associated to \(G\).

Example

Let \(G = (V,E)\) be the non-directed graph such that

\(V = \{0,1,2,3\}\) ; et

\(E = \{\{0, 1\}, \{1, 3\}, \{0, 2\}, \{1,2\} \}\).

When we want to draw a non-directed graph, we represent each edge by a line without any arrow connecting two vertices. We can thus draw the above graph as follows.

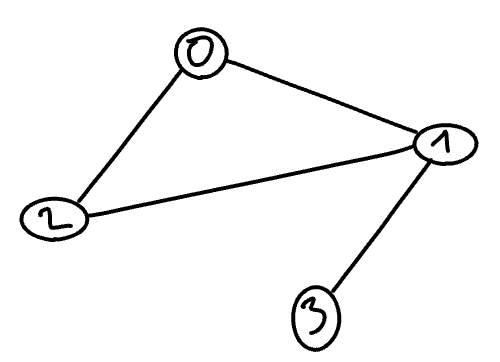
Graphical representation of a non-directed graph

The directed graph associated to \(G\) is draw below.

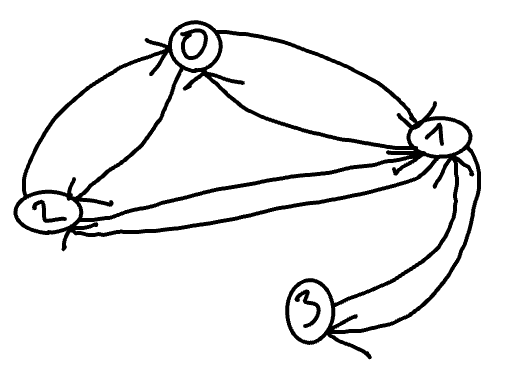
Let \(G\) be the graph of the previous example, indicate for each of the following statements wheter it is true (V) or false (F).

\(\{0,1\}\) is an edge of \(G\).
\(\{1,0\}\) is an edge of \(G\).
\((0,1)\) is an edge of \(G\).
\((1,0)\) is an edge of \(G\).
\(0\) is in \(\Gamma_G(1)\).
\(1\) is in \(\Gamma_G(0)\).
1 is adjacent to 3.
3 is adjacent to 1.
0 is adjacent to 3.

Fill in the following statements with the correct numerical value:

The graph \(G\) has edges.
The directed graph associate to \(G\) has arcs.

Definition: Weighted graph

Let \(G =(V,E)\) be a non-directed graph

A map associating a real number to each element of \(E\) is called a weight-map of \(G\)

If \(w\) is a weight-map of \(G\)

for each edge \(u\) of \(G\), the value \(w(u)\) is called the weight of \(u\); and

the pair \((G,w)\) is called a weighted graph.

In some cases, we rather use the term of value or of cost instead of weight.

Example

Let \(G = (V,E)\) be the non-directed graph such that

\(V = \{0,1,2,3\}\); and

\(E = \{\{0, 1\}, \{1, 3\}, \{0, 2\}, \{1,2\} \}\).

Let \(w\) be the map from \(E\) into the set of real numbers defined by

\(w(\{0,1\}) = 12\) ;

\(w(\{1,3\}) = 0.5\) ;

\(w(\{0,2\}) = 1\) ; and

\(w(\{1,2\}) = -7\).

The pair \((G,w)\) is thus a weighted graph. The weight of the edge \(\{0,1\}\) is 12, the one of \(\{1,3\}\) is 0.5, the one of \(\{0,2\}\) is 1, and the one of \(\{1,2\}\) is -7. This weighted graph can be drawn as follows.

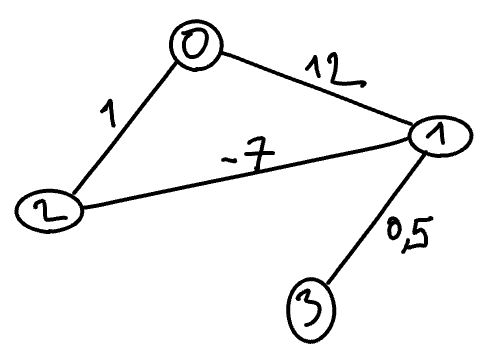
Graphical representation of a weighted graph

Exo - Sending a secret message without redundancy¶

Propose, for the case of the toy example, a transmission scheme of a secret message such that we have the guarantee that each spy receives the message only once (in this sense we say that the transmission is without redundancy). Explain your proposal in natural language. For this exercise, we do not take into account the interception probabilities of messages.

Reformulate your proposition using the terminology of graph theory.

How many sendings are necessary (and sufficient) for each spy to receive the message? Justify your answer using a proven property on graphs.

By adding a single line of instruction in the Breadth-first search algorithm, propose a Arboresence Algorithm which

given a strongly connected graph \(G = (V,A)\) and a vertex \(r\)

computes a subgraph \(G' = (V, A')\) of \(G\) (that is to say, \(A' \subseteq A\)) that is an arborescence of root \(r\). This arborescence will be reprsented in the form of a predecessor array..

Your proposal must be given in pseudo-language using the formalism of the algorithms presented in the previous workshops. In particular, you pay a particular attention to describe, in addition to the rest of the instructions, the input data and the produced results.

Implement the previous algorithm. To do this, create a function arborescence in a file arborescence.c. This function must return the arborescence structure in the form of an array “pred”. To this end, you must

copy the file explorationLargeur.c implemented during the exploration of graphs workshop and

transform the function explorationLargeur into arbrorescence based on the algorithm proposed just before.

Use your implementation to print a list of “communications” to establish between the spies in order to broadcast a secret message without redunduncy.

For each communication, you will print the sender and receiver of the message

To do this, you must first create a file (‘’.graphe’’) to store the graph which models the data of the toy example

As we are not interested here in the interception probabilities, it is not necessary to include the weight of the arcs in your file.

Also, you can save the graph as an asymmetric graph, but in this case, in your program, do not forget, after reading the graph from the file, to extract its symmetric closure before computing the arborescence.

Course - Trees and arborescences¶

Tree and arborescence structures are useful in many applications and are ubiquitous in computer science. For instance, we can quote:

the arborescences of files and directories;

the process-creation tree in an operating system;

phylogenic tree: kinship relationship between living species ;

search trees and arborescences, that can be binary, balanced, red and black, etc.;

decision tree;

tree structure for evaluating an arithmetic expression and more generally a syntactic tree;

hierarchical organization of a company, or of data of any kind;

mind map;

etc.

Intuitively, a tree is a graph whose drawing makes us think of a tree in botany in the sense that each branch is connected to the tree only by one of its ends. In other words, there cannot be any cycle in a tree.

In this section, we present a definition of a tree and of an arborescence, and we study some of their characteristic properties. We end the section by showing that it is possible to represent a tree structure with a simple array.

Introduction remark. In this section, every considered graphs is asymmetric (i.e., if the pair \((a,b)\) is an arc than \((b,a)\) is not an arc). Therefore, in order to ease the reading, in this section (and only in this section), we will omit this precision when talking about a graph: we will use the word “graph” instead of “asymmetric graph”.

Trees¶

Definition: Tree

A tree is a connected graph in which there is no cycle.

Let \(G_1, \ldots, G_6\) be the six following graphs. For each of them, indicate in the table below (V for True and F for False), if it is a tree, if it is connnected and if it is without cycle.

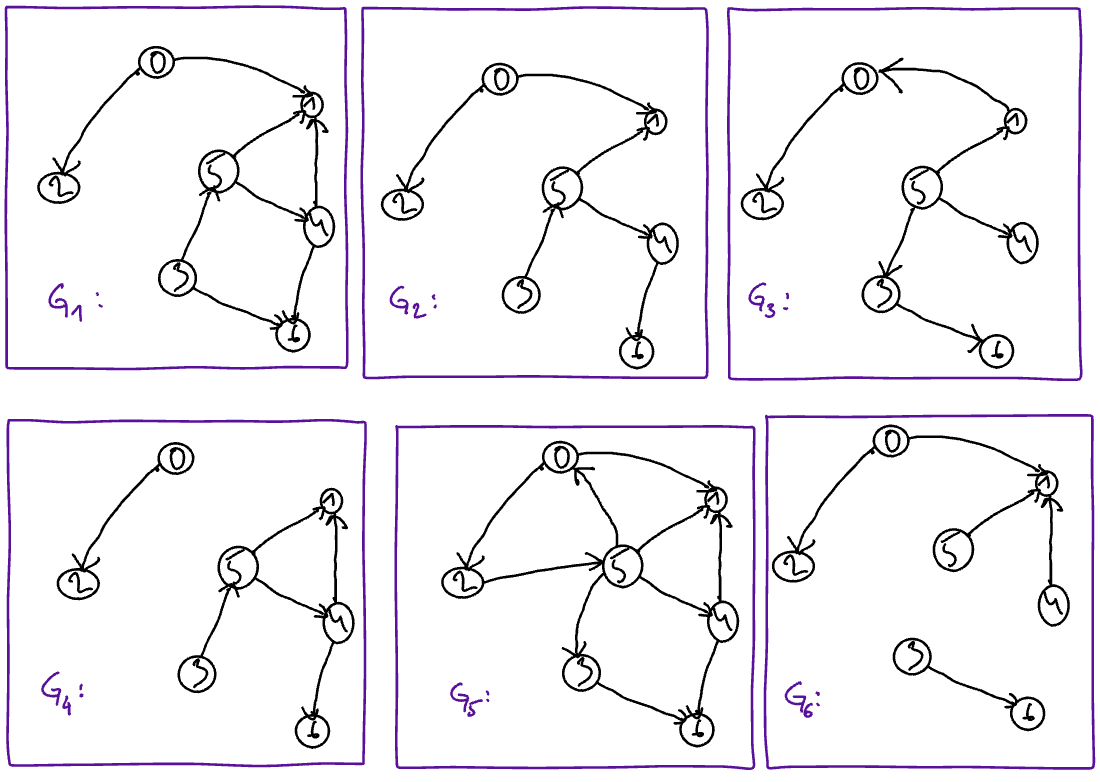
Examples of graphs, some of which are trees

	is a tree	is without cycle	is connected
\(G_1\)
\(G_2\)
\(G_3\)
\(G_4\)
\(G_5\)
\(G_6\)

A tree can be characterized (i.e., equivalently defined) in different ways. The next property presents four standard characterizations of trees. These characterizations allow us to better understand what a tree is. They also offer us different possibilities to recognize that a graph is a tree. Depending on the context, it is sometimes easier to use one characterization than another.

Property

Let \(G\) be a graph with \(n\) vertices. The four following statements are equivalent:

\(G\) is a tree;

\(G\) is connected and the bnumber of arcs of \(G\) is equal to \(n-1\) ;

\(G\) is without cycle and the number of arcs of \(G\) is equal to \(n-1\) ;

for every pair of two vertices \(x\) and \(y\) of \(G\), there exists a unque elementary chain from \(x\) to \(y\).

A remarkable consequence of this property is that the number of arcs of a tree is always equal to the number of its vertices minus 1.

In order to establish the proof of this property, we introduce the notion of isthmus in a graph.

Definition: isthmus

Let \(G =(V,A)\) be a graph and let \(u\) be an arc of \(G\). We say that \(u\) is an isthmus of \(G\) if \(u\) does not appear in any cycle of \(G\).

Let \(G_1, \ldots, G_3\) be the three following graphs.

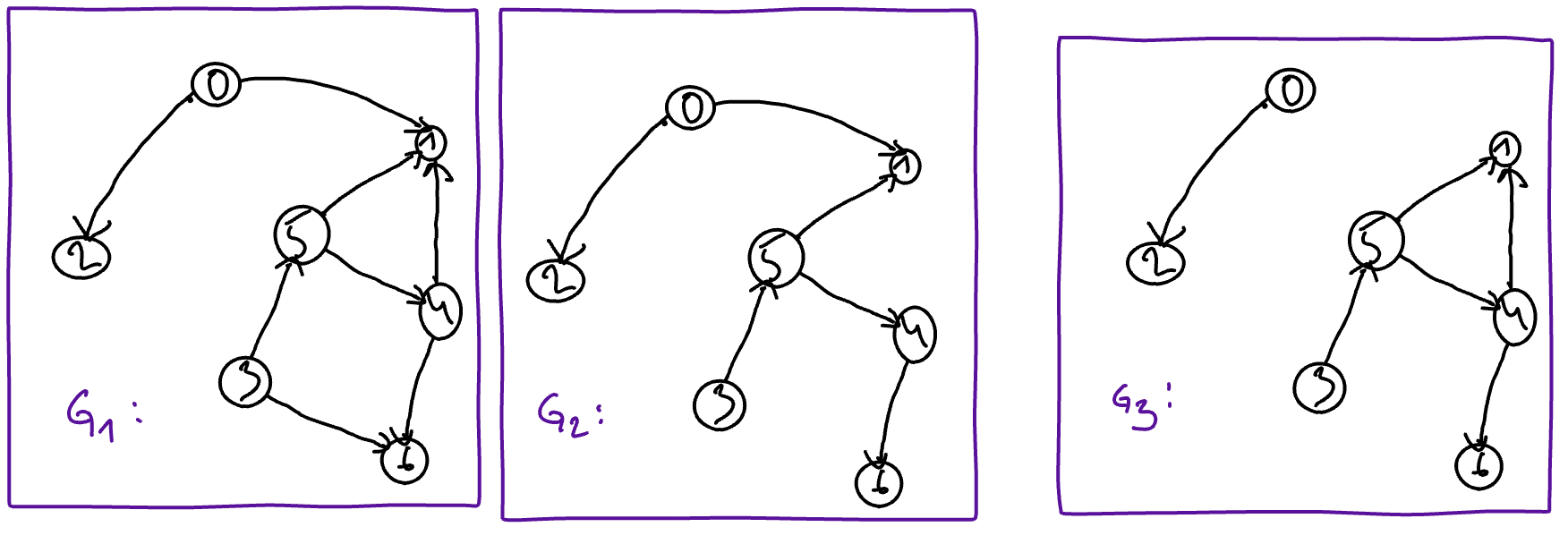
For each of the following statements, indicate whether it is true (V) or false (F).

\((0,2)\) is an isthmus of \(G_1\)

\((0,1)\) is an isthmus of \(G_1\)

\((5,1)\) is an isthmus of \(G_1\)

\((4,1)\) is an isthmus of \(G_1\)

\((5,4)\) is an isthmus of \(G_1\)

\((3,5)\) is an isthmus of \(G_1\)

\((3,6)\) is an isthmus of \(G_1\)

\((4,6)\) is an isthmus of \(G_1\)

Fill in the 3 following statements in order to make them hold true.

The graph \(G_1\) has isthmus.

The graph \(G_2\) has isthmus.

The graph \(G_3\) has isthmus.

We can observe that if we remove an arc \(u =(a,b)\) from a graph \(G = (V,A)\), we obtain a graph \(G' = (V, A \setminus \{u\})\) such that:

the numbers of connected components of \(G\) and \(G'\) are equal if \(u\) is not an isthmus of \(G\); et

the number of connected component of \(G'\) is exactly one more than the number of connected components of \(G\) if \(u\) is an isthmus.

Thus, we can deduce that if we sequentially remove all the arcs of a connected graph \(G\) with \(n\) vertices, during the sequence, we have to remove exactly \(n-1\) isthmus since the final graph, without arc, has exactly \(n\) connected components (one for each vertex). We may thus affirm that:

[P1] a connected graph contains at least \(n-1\) arcs.

Moreover, we can observe that a graph with \(n\) vertices has at most \(n-1\) isthmuses (otherwise, by removing successively all these isthmuses, we would obtain a graph with strictly more than \(n\) connected components, which is a contradiction since the graph only has \(n\) vertices). As in a graph without cycle, any arc is an isthmus we can also affirm

[P2] a graph without cycle has at most \(n-1\) arcs.

With the help of these two statements in bold, it is possible to prove the characterizations of a tree presented in the previous property.

Preuve (pour les curieux, en français pour l’instant).

Pour démontrer que les quatre affirmatioins de la propriété précédente sont équivalentes, nous allons montrer que la première affirmation implique la seconde, que la seconde implique la troisième, que la troisième implique la quatrième et que la quatrième implique la première.

(\((1) \Longrightarrow (2)\)) Démontrons tout d’abord que l’affirmation 1 implique l’affirmation 2. Pour cela, nous supposons que \(G\) est un arbre, c’est-à-dire que :

\(G\) est connexe et sans cycle ;

D’après l’affirmation P2 ci-dessus, ceci implique que :

\(G\) est connexe et possède au plus \(n-1\) arcs.

De plus, comme \(G\) est connexe, d’après l’affirmation (P1), \(G\) contient au moins \(n-1\) arcs, ce qui nous permet de conclure que

\(G\) est connexe et possède exactement \(n-1\) arcs

(\((2) \Longrightarrow (3)\)) Nous allons maintenant démontrer que l’affirmation 2 implique l’affirmation 3. Pour cela nous supposons que :

\(G\) est connexe et possède exactement \(n-1\) arcs.

Chaque arc \(u\) de \(G\) est un isthme. En effet, d’après (P1), le graphe \(G' = (S, A \setminus \{u\})\) ne peut être connexe puisqu’il contient \(|A|-1= n-2\) arcs, donc, comme \(G\) est connexe, d’après les observations qui suivent la définition d’un isthme, nous déduisons que \(u\) est un isthme. Ainsi, aucun arc de \(G\) n’apparaît dans un cycle, ce qui implique que le graphe \(G\) est sans cycle. En d’autre termes, l’affirmation suivante est vraie :

\(G\) est sans cycle et contient \(n-1\) arcs.

(\((3) \Longrightarrow (4)\)) Démontrons maintenant que l’affirmation (3) implique affirmation (4). Pour cela, nous supposons que

\(G\) est sans cycle et contient \(n-1\) arcs.

Comme \(G\) est sans cycle, chaque arc de \(G\) est un isthme. Soit une séquence \((G_1 = G, \ldots, G_{n})\) de graphes obtenues en supprimant successivement chacun des arcs de \(G\) (pris dans n’importe quel ordre). D’après l’observation énoncée après la définition d’un isthme, on peut affirmer que \(G_i\) possède exactement une composante connexe de plus que \(G_{i-1}\). Ainsi, \(G_{n}\) possède exactement \(n-1\) composantes composantes connexes de plus que \(G_{1}\). Comme \(G_n\) ne peut avoir plus de \(n\) composantes connexes (car il possède \(n\) sommets), et que \(G_1\) ne peut en avoir moins que une, nous déduisons que \(G_1 = G\) possède une unique composante connexe, c’est à dire que \(G\) est connexe. Ainsi, pour tous sommets \(x\) et \(y\), il existe une chaine élémentaire \(\pi\) de \(x\) à \(y\). De plus, comme \(G\) est sans cycle, nous pouvons observer qu’il n’existe pas d’autre chaine élémentaire de \(x\) à \(y\) (s’il existait une autre chaine \(\pi'\) de \(x\) à \(y\) alors \(G\) posséderait un cycle voir dessin ci-dessous).

(\((4) \Longrightarrow (1)\)) Démontrons maintenant que l’affirmation (4) implique affirmation (1). Nous supposons donc ici que :

pour toute paire de sommets \(x\) et \(y\) de \(G\), il existe une unique chaine élémentaire de \(x\) à \(y\) ;

Donc, nous pouvons affirmer que \(G\) est connexe. Pour compléter la preuve que \(G\) est un arbre, il reste donc à montrer qu’il n’y a pas de cycle dans \(G\). Pour cela, il est suffisant de montrer que chaque arc de \(G\) est un isthme. Soit \(u = (x,y)\) un arc quelconque de \(G\). Nous allons procéder par l’absurde pour montrer que \(u\) est un isthme, c’est à dire que nous allons supposer que \(u\) n’est pas un isthme et nous allons montrer que cela contredit notre hypothèse (que l’affirmation (4) est vraie). Si \(u\) n’est pas un isthme, il existe alors un circuit qui passe par \(u\). Donc, il existe une chaîne élémentaire \((x_0 = x , x_1 = y, \ldots, x_\ell = x)\) de longueur au moins 3. Ainsi, la séquence \((x_1 = y, \ldots, \x_ell=x)\) est une chaine élémentaire de \(y\) à \(x\) de longueur au moins 2. Comme \((y,x)\) est une chaîne élémentaire de \(y\) à \(x\) de longueur 1, cela signifie qu’il existe deux chaines élémentaires distinctes de \(y\) à \(x\), ce qui est en contradiction avec notre hypothèse. CQFD

Arborescences¶

Definition: Roots and arborescences

Let \(G =(S,A)\) be agraph and let \(r\) be a vertex of \(G\).

We say that \(r\) is a root of \(G\) if every vertex of \(G\) can be reached by a path from \(r\), that is, if :

\(\mbox{Expl}(G,r) = S\)

We say that \(G\) is an arborescence of root \(r\) if \(G\) is a tree and if \(r\) is a root of \(G\).

Let \(G_1, \ldots, G_6\) be the six following graphs.

Fill in the 6 following statements to make them hold true.

The graph \(G_1\) has root(s).

The graph \(G_2\) has root(s).

The graph \(G_3\) has root(s).

The graph \(G_4\) has root(s).

The graph \(G_5\) has root(s).

The graph \(G_6\) has root(s).

State, for each of the following statement wether it is true (V) or false (F).

The graph \(G_1\) is an arboresence.

The graph \(G_2\) is an arboresence.

The graph \(G_3\) is an arboresence.

The graph \(G_4\) is an arboresence.

The graph \(G_5\) is an arboresence.

The graph \(G_6\) is an arboresence.

We can observe that if \(G\) is an arborescence of root \(r\), then \(r\) is the only vertex of \(G\) that is a root (otherwise there would be a cycle, which is a contradiction with the fact that \(G\) is a an arborescence, and thus a tree).

The next property characterizes the arborescences. This characterization leads in particular to a very compact representation of arborescences with the help of an array of predecessors.

Property

Let \(G =(V,A)\) be a graph with \(n\) vertices. The two folloing statements are equivalent:

\(G\) is an arborescence of root \(r\); and

\(r\) is a root of \(G\) that does not have any predecessor and each vertex in \(S \setminus \{r\}\) has a unique predecessor.

Preuve (pour les curieux, en français).

Démontrons d’abord l’implication directe. Pour cela, nous allons montrer que si l’affirmation 1 est vraie alors l’affirmation 2 l’est également. Nous supposons donc que l’affirmation 1 est vraie. D’après la définition d’une arborescence, cela signifie que \(G\) est un arbre. Donc d’après la propriété caractéristique des arbres, cela implique que \(G\) contient exactement \(n-1\) arcs. Comme \(r\) est une racine, il existe un chemin non trivial de \(r\) à chaque sommet \(x\) dans \(S \setminus \{r\}\). Ainsi chaque sommet de \(S \setminus \{r\}\) possède au moins un prédécesseur. Comme \(S \setminus \{r\}\) contient \(n-1\) sommets et que \(G\) contient \(n-1\) arcs, nous déduisons que chaque sommet \(S \setminus \{r\}\) possède exactement un prédécesseur et que \(r\) n’a pas de prédécesseur.

Démontrons maintenant l’implication réciproque, c’est-à-dire que l’affirmation 2 implique l’affirmation 1. Pour cela, nous supposons donc désormais que l’affirmation 2 est vraie. Comme \(r\) est une racine de \(G\), pour démontrer que l’affirmation 1 est vraie, il suffit de prouver que \(G\) est un arbre. Pour cela, nous allons montrer que

(i) \(G\) est connexe et que

(ii) \(G\) possède \(n-1\) arcs

ce qui d’après la propriété caractéristique des arbres est suffisant pour affirmer que \(G\) est un arbre. Pour démontrer que la proposition (i) est vraie nous allons montrer que toute paire de sommets \(x\) et \(y\) est liée par une chaine. Soient \(x\) et \(y\) deux sommets de \(G\). Comme \(r\) est une racine de \(G\), il existe un chemin de \(r\) à \(x\) dans \(G\) ainsi qu’un chemin de \(r\) à \(y\). D’après la définition d’une chaine, il existe ainsi une chaine de \(x\) à \(r\) et une chaine de \(r\) à \(y\). La concaténation de ces deux chaines est donc une chaine de \(x\) à \(y\), ce qui complète la preuve que (i) \(G\) est connexe. Montrons maintenant que la proposition (ii) est également vraie. Pour cela, il convient d’abord d’observer que le nombre d’arcs de \(G\) est égal à la somme des nombres de prédécesseurs de chaque sommet du graphe. Comme le graphe \(G\) comprend

\(n-1\) sommets qui ont exactement un prédécesseurs (chaque sommet de l’ensemble \(S \setminus \{r\}\) ) et

1 sommet sans prédécesseur (le sommet \(r\)),

nous déduisons que \(G\) possède \(n-1\) arcs. CQFD

Memory representation of an arborescence¶

An arborescence \(G =(V,A)\) of root \(r\) can be represented with a simple array. Let \(V = \{0, \ldots, n-1\}\) be the set of vertices of this arborescence, then, from the characterization of the arborescences presented in the previous section, we can define the array pred of size \(n\) by

pred[x] = NULL if \(x = r\); and

pred[x] = y where \(y\) is the unique predecessor of \(x\) if \(x \neq r\).

We can observe that the array pred allows us to recover all the arcs of the arboresence \(G\), that is the set

\(A = \{ (pred[x],x)~|~x \in S \text{ such that } pred[x] \neq NULL\}\).