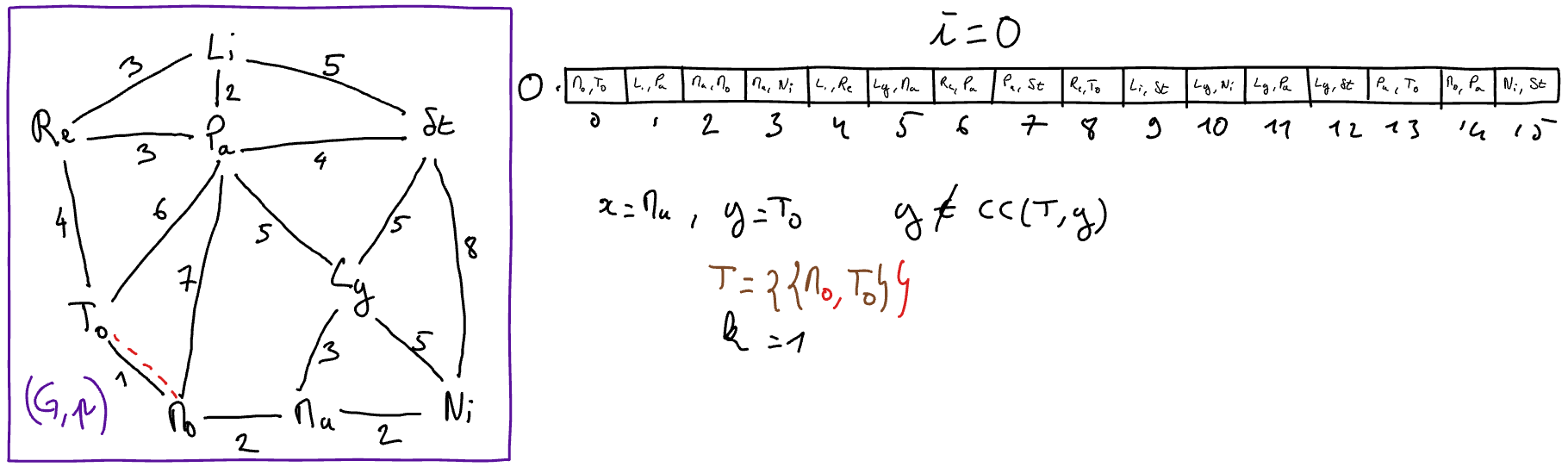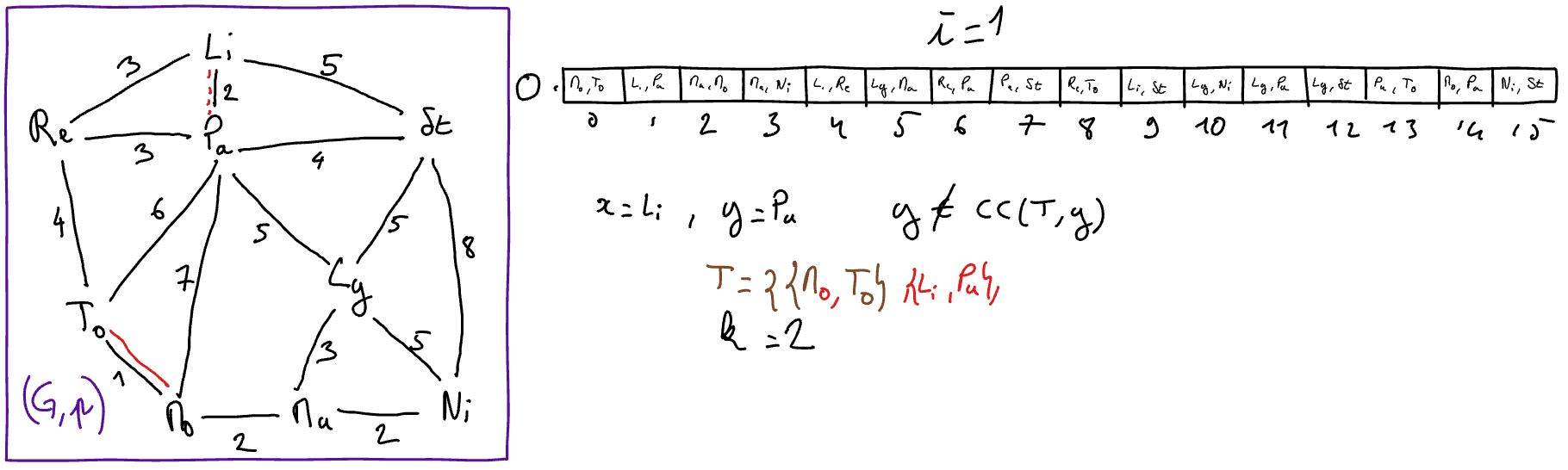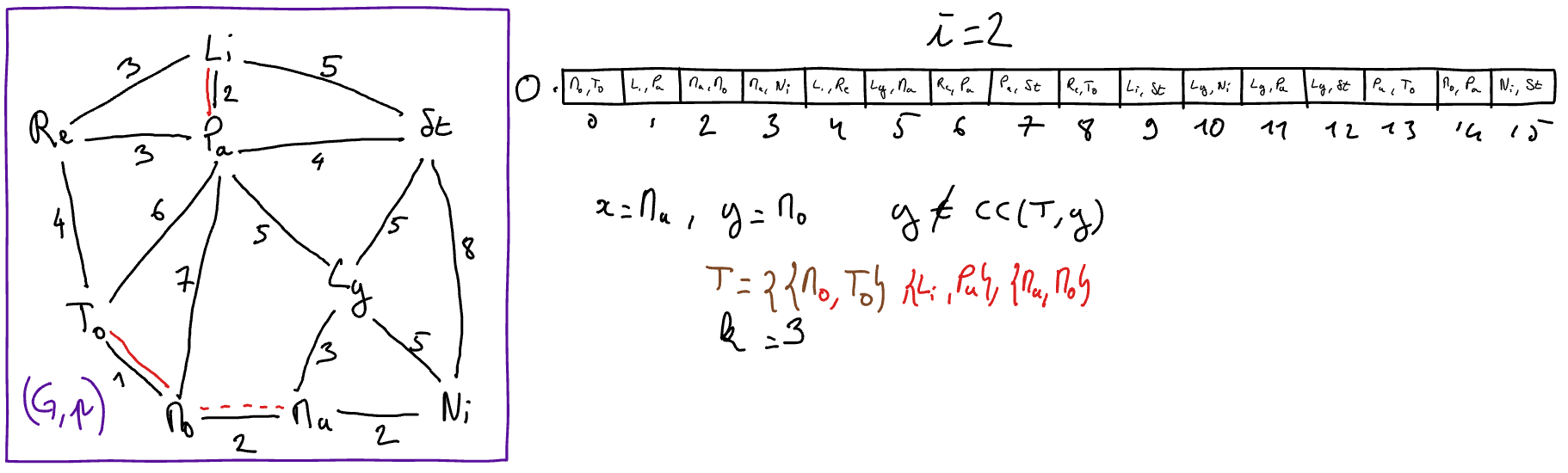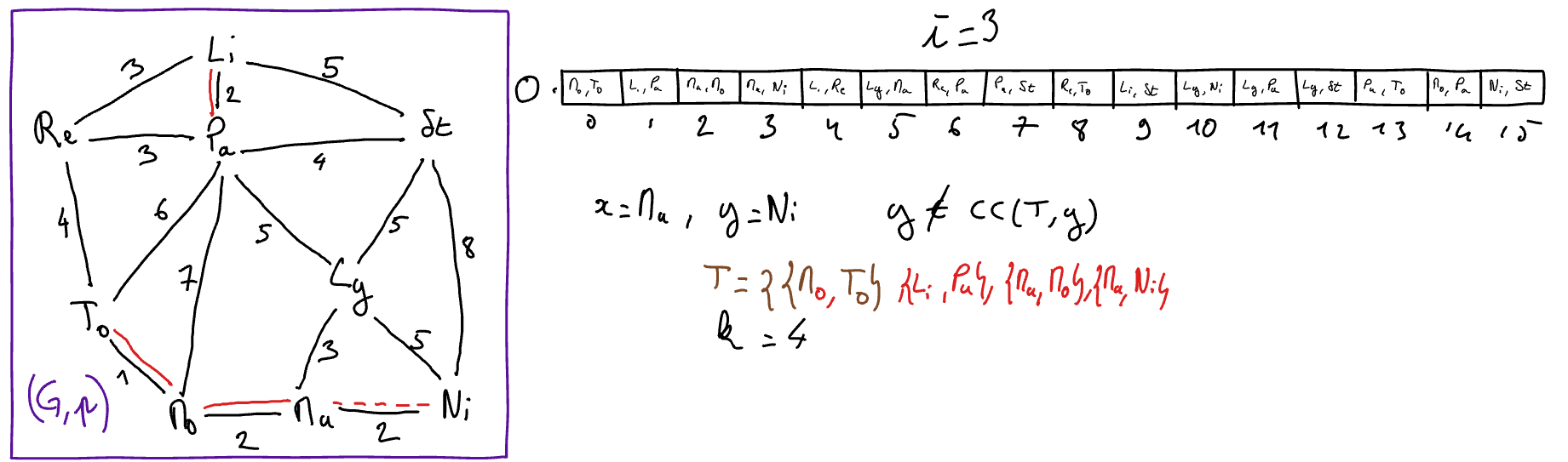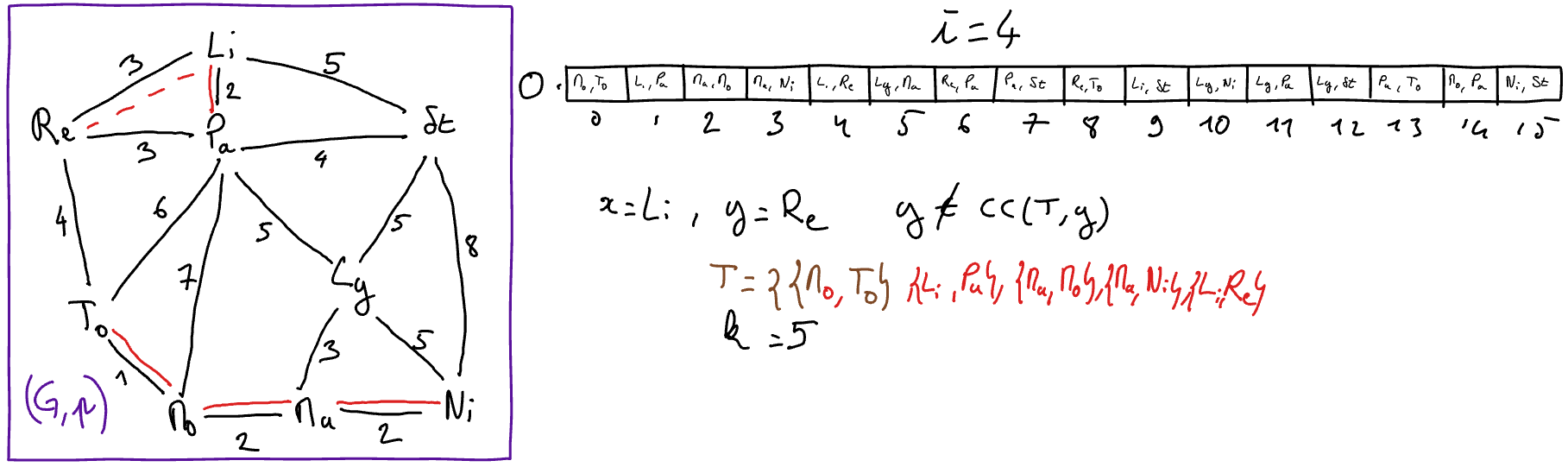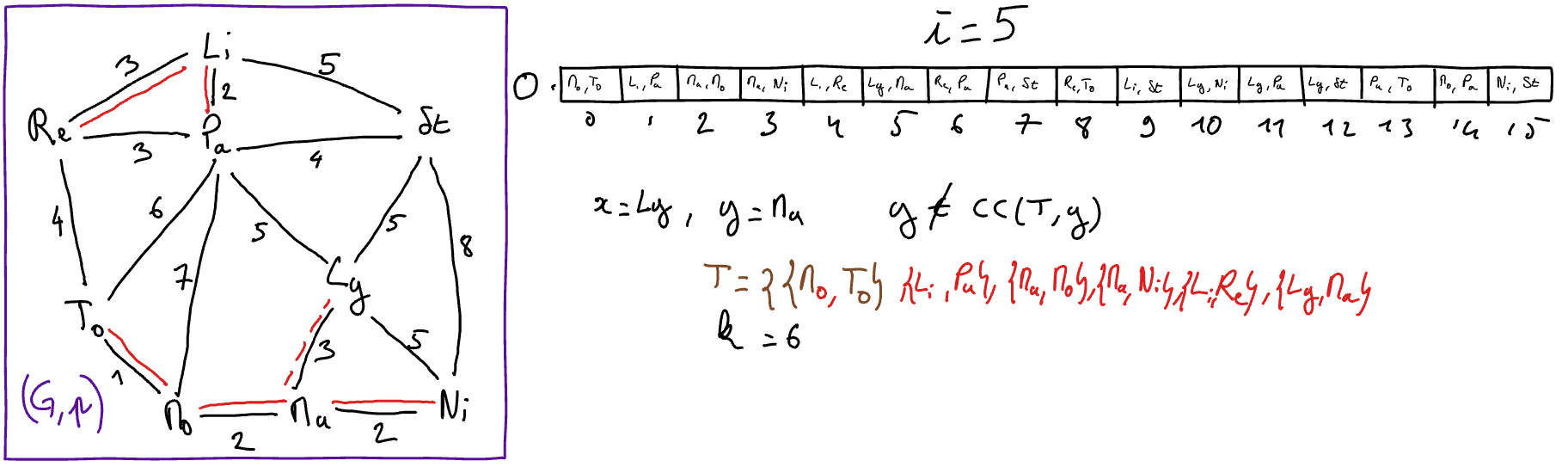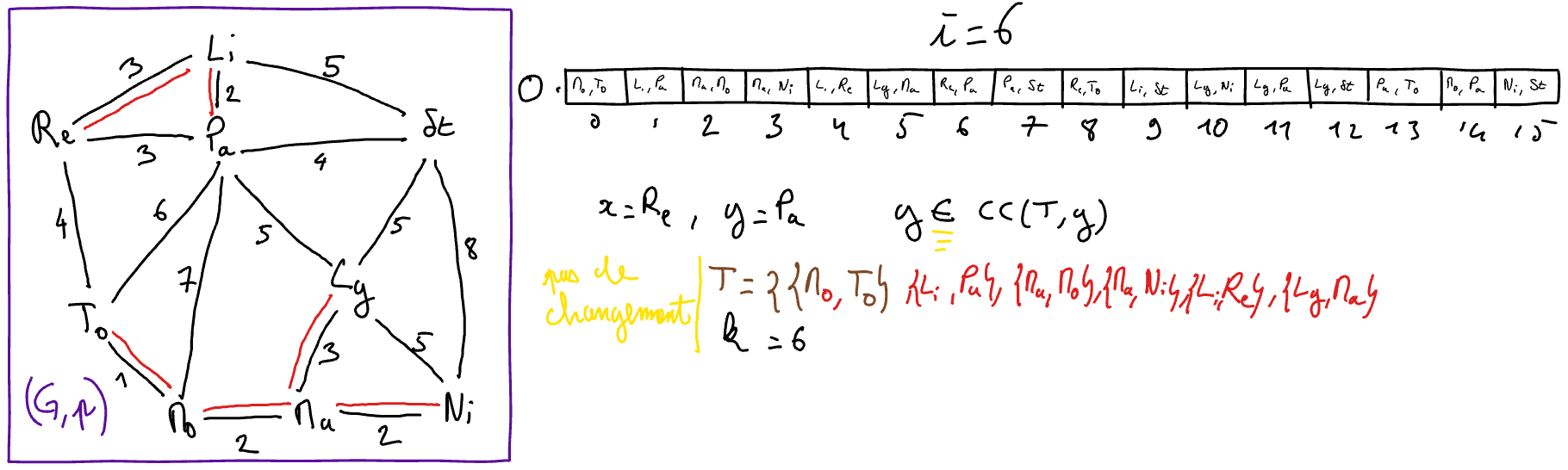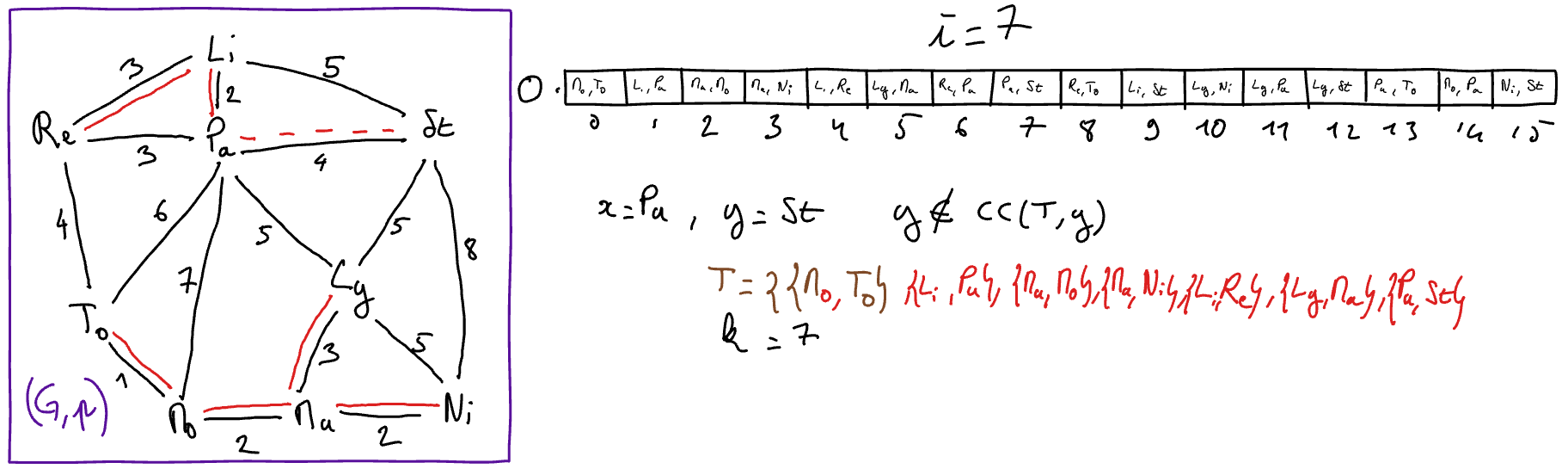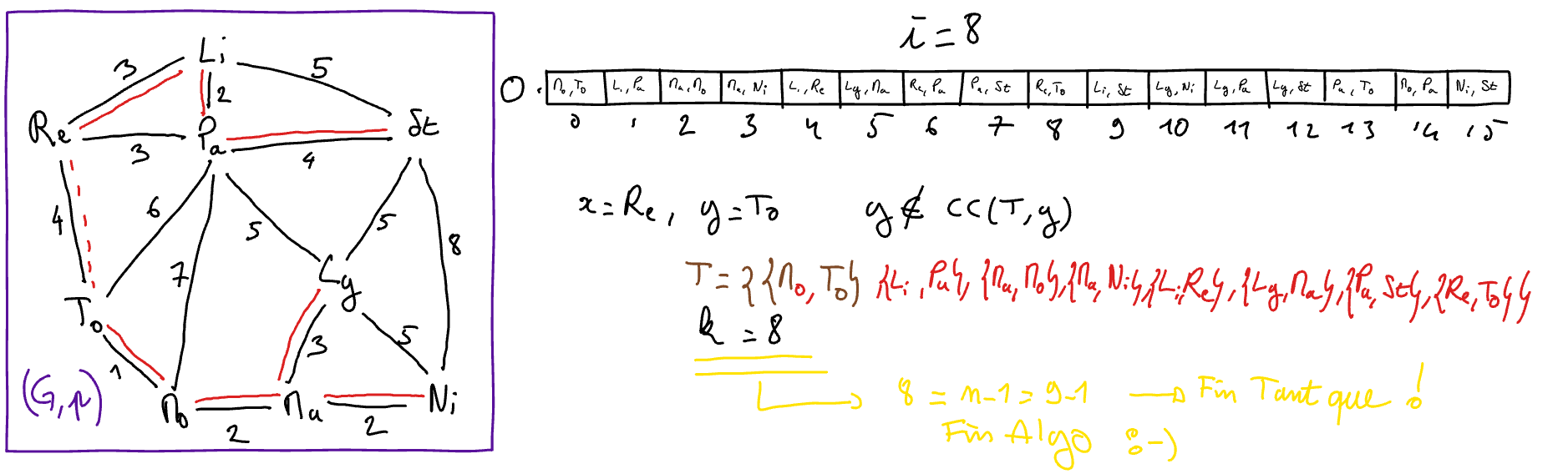Building and optimizing a spy network - part 2: minimum spanning tree

Common thread

The secret services must establish a spy network. More precisely, they have to establish a routing plan for secret messages such that a given spy can send information to a group of \(N\) other spies. Among this group of spies, some have the possibility of contacting each other and directly exchanging information while others cannot. When two spies exchange a message, the message can be intercepted with some known probability. In this course, we will answer the following questions:

  • How a message can be sent to all the members of the network?

  • How to carry out these communications while minimizing the probability that the message be intercepted?

In order to carry out this study, we will answer the following questions:

  • How should we model the data of the problem?

  • How can we select an optimal solution, (that is to say for which the probability of interception is minimal) among all possible solutions?

In order to answer these questions,

  • we introduced, in part 1, the notion of an (edge-)weighted graph; and

  • we studied the notions of a tree and of an arborescence;

  • in this part, we will consider the problem of finding a minimum spanning tree and we will study Kruskal algorithm to solve it.

Organization of the course

Every section with a title labeled “Exo” refers to exercises related to the common thread problem. You must individually answer all these questions and record your answers in a report of your own. To this end, you have to

  • create an individual google doc;

  • share it with the teacher from the beginning of the session .

For questions that require code, you will be asked to copy the code you produced into your report. For this type of questions, you will not be asked to write an entire program on your own but to complete a graph library written in C. Thus, you should never have to produce more than twenty lines of code per question.

The produced report will be used for your evaluation in the “Graphs and Algorithms” course.

In general, each section labeled “Exo” is followed by a section labeled “Course” which presents the concepts necessary to answer the questions related to the common thread problem.

In the flow of the course sections, you will also find small quizzes which aim to test your understanding of the course. To check your answers, all you have to do is click on the “correct” button at the end of the exercise.

This course is not a mooc! A teacher is here to help you: call him whenever you have the slightest doubt or to check your answers. The teacher can also enter comments directly in your report. Take these remarks into account to improve your answers.

A “toy example”

Let us consider 9 spy-agents numbered from (00)0 to (00)9, the spy 007 must send a message to the other nine. To this end, the following communication exchanges are possible:

  • between spies 0 and 9 with an interception probability of 0.3%

  • between spies 0 and 3 with an interception probability of 0.6%

  • between spies 0 and 2 with an interception probability of 0.2%

  • between spies 1 and 3 with an interception probability of 0.3%

  • between spies 1 and 4 with an interception probability of 0.4%

  • between spies 1 and 6 with an interception probability of 0.3%

  • between spies 1 and 9 with an interception probability of 0.4%

  • between spies 2 and 5 with an interception probability of 0.6%

  • between spies 2 and 7 with an interception probability of 0.5%

  • between spies 3 and 7 with an interception probability of 0.2%

  • between spies 4 and 6 with an interception probability of 0.2%

  • between spies 4 and 8 with an interception probability of 0.4%

  • between spies 5 and 7 with an interception probability of 0.1%

  • between spies 5 and 8 with an interception probability of 0.2%

Exo - Optimal solution for the toy example

  • For each exercise in this second part of the workshop, it is assumed that message interceptions are independent events.

  1. For the case of the toy example, propose a scheme for broadcasting a secret message which minimizes the probability that the message will be intercepted. You do not need to justify here that your proposal is optimal (this will be the subject of a next question) or how you built this solution. Thus, we can here be satisfied with a solution of low interception probability (that is to say for which we cannot easily find an improvement).

  2. If we wanted to naively verify (with a brute force method) that the solution given above is optimal, how many graphs should we consider?

  3. Using the terminology of graph theory, state a valid solution for any set of spies and any set of possible communicatoins between them.

  4. Justify the your answer to the previous question. To help, you can rely your justifications on the foolowing reminders:

    • if \(A\) and \(B\) are two independent events of probabilities \(p_A\) and \(p_B\), respectively, then the probability of the event (\(A\) and \(B\)) is equal to \(p_A.p_b\)

    • if \(A\) is an event of probability \(p_A\), the probability of the event \((not~A)\) is \(1-p_A\)

    • the logarithm function \(ln\) is such that for any two real values \(a\) and \(b\), we have \(ln(a.b) = ln(a) + ln(b)\)

    • the logarithm function \(ln\) is increasing, meaning that for any tow real values \(a\) and \(b\) if \(a\) is less than \(b\) then \(ln(a)\) is less than \(ln(b)\).

  1. In the scheme that you proposed in question 1, give the probability that the message is intercepted.

Course - Minimum spanning tree

Finding a minimum spanning tree is one of the most typical and well-known problems in the field of combinatorial optimization. In this section, we will start by formulating this problem through a practical situaltion, then we will formalize it in terms of graphs and we will end with the presentation of the dual problem of the maximum spanning tree. In the next course section, we will study an efficient algorithm to solve this problem.

Situation

We want to build a (ultra-fast) communication network to connect the main French cities at high speed. We know the cost of building the following links:

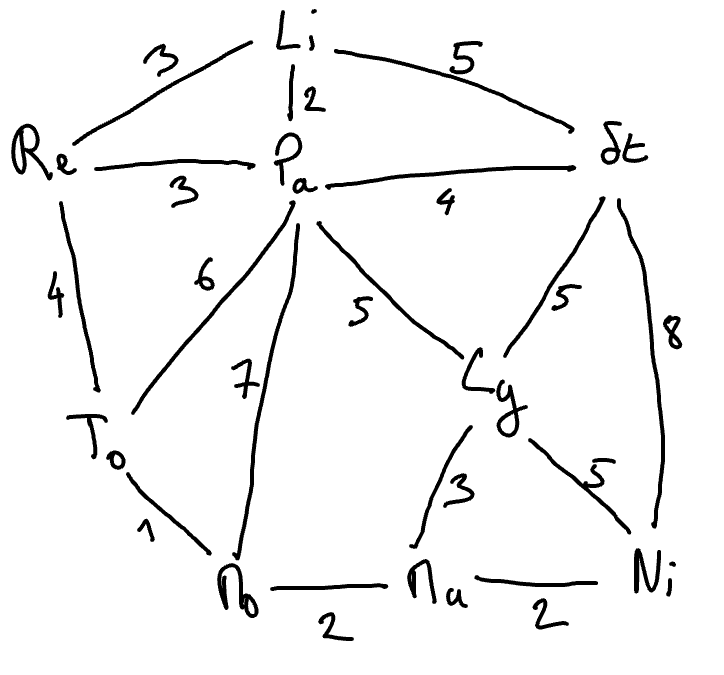
Graphical representation of a weighted graph
Probleme.

  • How can we build such a communication network at lowest possible cost while ensuring that information can be transmitted from any city to any other?

The solutions to this problem are called the minimum weight trees of the weighted graph drawn above.

Formalization with graphs

Intuitively, a solution to the problem stated above must satisfy the following conditions:

  1. be a subgraph of the initial graph modeling the data. Indeed only the edges of this initial graph correspond to links that can be built;

  2. in this subgraph, there must be a path from any city to any other in order propagate the information: this subgraph must therefore be connected and must contains every vertex of the initial graph ;

  3. among all the subgraphs which satisfy condition (1) and condition (2) above, we must keep a solution of cheapest cost.

The four definitions presented below allows one to formalize the four conditions written in bold above.

Important remark. In this part of the course, we only consider connected graphs weighted with (strictly) positive values, that is to say the weight of an edge is always greater than 0. In order to ease the reading, we will omit this precision when talking about a weighted graph.

Definition (spanning subgraph)

Let \(G = (V,E)\) be non-directed graph. A spanning subgrah of \(G\) is a graph \(G' = (V',E')\) whose vertex set if the same as the one of \(G\) and for which every edge is also en edge of \(G\), that is to say that \(G'\) is such that:

  • \(V' = V\) ; et

  • \(E' \subseteq E\).

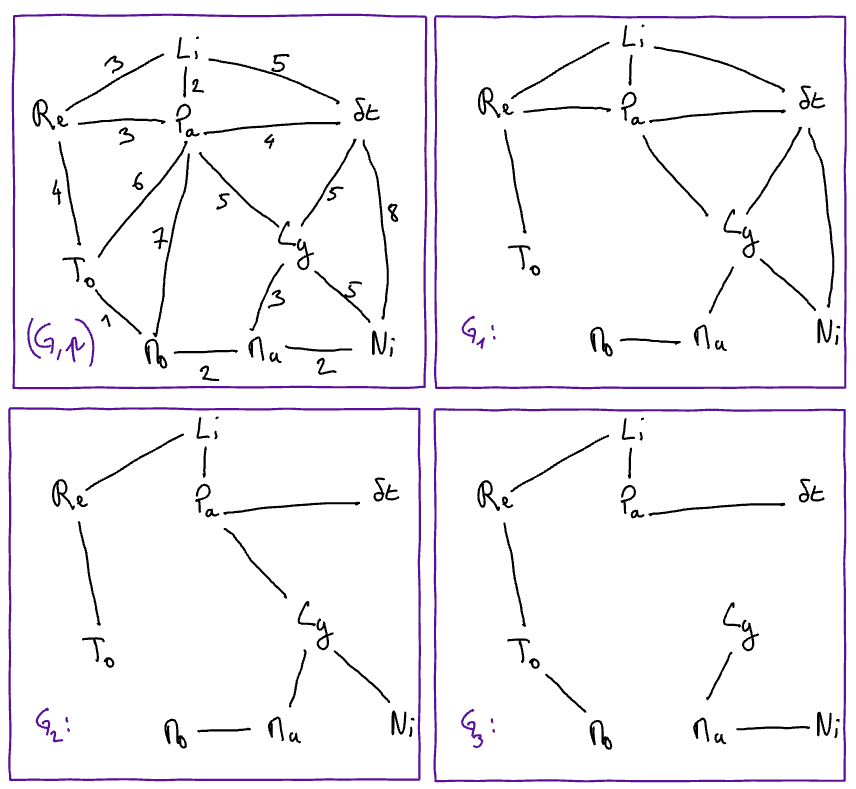
Let \(G, G_1, G_2, G_3\) be the following graphs

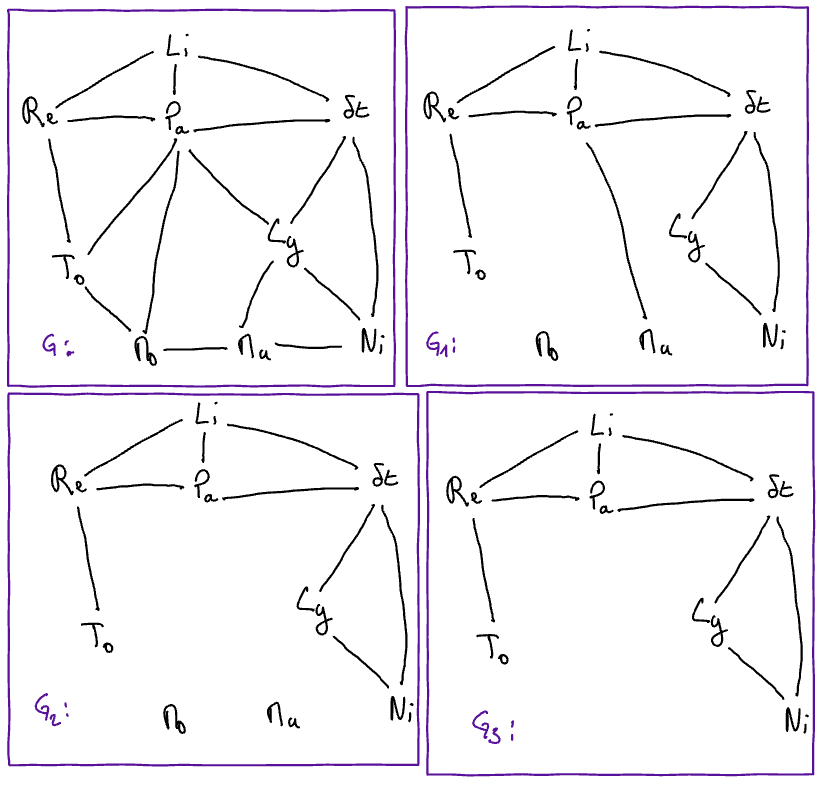
Example of graphs, some of which are spanning

Let us also consider:

  • \(G_4 = (S_4, A_4)\) with \(S4 = \{ Li, Pa, Ly, St, Re, Mo, Ma,\}\) and \(A_4 = \{ \{Li, Pa\}, \{ Pa, St\}, \{Pa, Re\} \}\); and

  • \(G_5 = (S_5, A_5)\) with \(S4 = \{ Li, Pa, Ly, To, St, Re, Mo, Ma, Ni\}\) and \(A_4 = \{ \{Li, Pa\}, \{ Pa, St\}, \{Pa, Re\} \}\).

State, for each of the following propositions, whether it is true (V) or false (F.

  • \(G_1\) is a spanning subgraph of \(G\)

  • \(G_2\) is a spanning subgraph of \(G\)

  • \(G_3\) is a spanning subgraph of \(G\)

  • \(G_4\) is a spanning subgraph of \(G\)

  • \(G_5\) is a spanning subgraph of \(G\)

Definition (reminder): connectivity

Let \(G = (V,E)\) be a non-directed graph. The graph \(G\) is connected, if the directed graph \((S, \Gamma_G)\) associated \(G\) is connected, that isn for every pair of vertices \(x\) and \(y\) of \(G\), there exists a chain from \(x\) to \(y\) in \((V, \Gamma_G)\).

Definition weight (of a weighted graph)

Let \((G,w)\) be a weighted graph such that \(G = (V,E)\). The weight of \(G\), enoted by \(W(G)\), is the sum of the weights of the edges of:math:G, that is to say

  • \(W(G) = \sum_{u \in E} w(u)\).

Let \((G,w)\) be the weighted graph et and let \(G_1, G_2\), and \(G_3\) be the subgraphs of \(G\) drawn below:

Weighted graphs and wpanning subgraphs

Fill in the following equalities to make them hold true

  1. \(P(G_1)=\)

  2. \(P(G_2)=\)

  3. \(P(G_3)=\)

Definition minimum spanning tree

Let \((G,w)\) be a weighted graph. A minimum spanning tree (of \((G,w)\)) is a graph \(G'\) such that:

  1. \(G'\) is a subgraph of \(G\);

  2. \(G'\) is connected;

  3. the weight of \(G'\) is minimum among the weights of the graphs satisfyong both conditions 1 and 2 above, that is to say

    • for any connected subgraph \(G''\) taht is spanning for \(G\), we have \(W(G') \leq W(G'')\).

Let \((G,w)\) be the weighted graph and let \(G_1, G_2, G_3, G_4\), and \(G_5\) be the subgraphs of \(G\) drawn below.

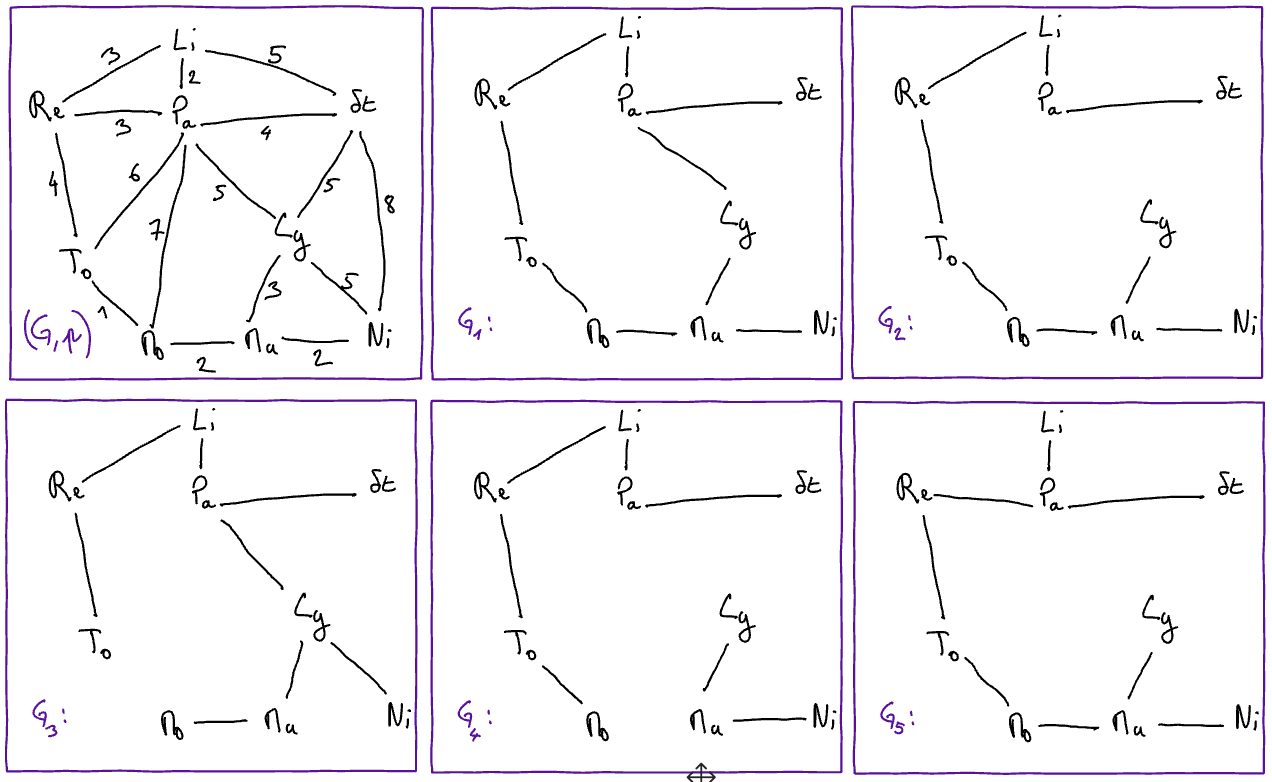
Weighted graphs and spanning subgraphs

State, for each of the following proposition, whether it is true (V) or false (F) (help: there is at least on proposition that holds true).

  • \(G_1\) is a minimum spanning tree of \((G,w)\)

  • \(G_2\) is a minimum spanning tree of \((G,w)\)

  • \(G_3\) is a minimum spanning tree of \((G,w)\)

  • \(G_4\) is a minimum spanning tree of \((G,w)\)

  • \(G_5\) is a minimum spanning tree of \((G,w)\)

The previous definition does not explicitly require that a minimum spanning tree be a tree. However, we can observe that a connected graph \(G'\) that is not a tree cannot be a minimum spanning tree. Indeed, such a graph necessarily contains an edge which is not an isthmus (otherwise it would be a tree) and the deletion of which leads to a connected graph of weight strictly less than the weight of \(G'\), thus completing the proof that \(G'\) is not a minimum spanning tree. We can therefore deduce the following property.

Property

Let \((G,w)\) be a weighted graph. Any minimum spanning tree of \((G,w)\) is a tree.

Remark

  • Given a weighted \((G,w)\), there may exist several distinct minimum spanning trees. For example, in the case of a graph where all the weights are equal (and are equal to 1), each spanning subgraph which is a tree is also a minimum spanning tree (of weight \(n-1\) if \(n\) is the number of vertices of G).

  • If there are several minimum spanning trees of \((G,w)\), the weight of each of these trees is the same.

In the field of combinatorial optimization, for a given weighted graph \((G,w)\),

  • the set \(\mathcal{R}\) containing the connected and spanning subgraphs of \(G\) is called the set of admissible solutions (of the problem) ;

  • the function \(P\) that maps its weight to every graph in \(\mathcal{R}\) is called the objective function; and

  • the problem itself consists of determinig the value

    • \(\min \{ P(G')~|~ G' \in \mathcal{R}\}\).

To solve this problem, a naive solution (“brute force method”) consists in:

  1. list all the spanning subgraphs of \(G\) ;

  2. check, for each of them, if it is connected (and therefore if it belongs to the set \(\mathcal{R}\)) ; and if it is the case

    1. compute its weight; and

    2. keep the cheapest weight

This naive algorithm is not very efficient since there is a very large number of subgraphs of \(G\) and therefore enumerating them all would take a long time. More precisely, if \(G\) is made of \(m\) edges, this number is equal to \(2^m\). Indeed, each edge of \(G\) can be included/excluded in/from a subgraph, listing all the subgraphs of \(G\) reduces to enumerating all the binary words of \(m\) bits (1 bit per edge). Thus, the complexity of the naive algorithm is at least exponential in \(O(2^m)\). In practice, it is not possible to use such an algorithm for a graph of more than a few dozens of vertices. In a next section, we will see a very efficient algorithm to solve this problem in time \(O(nm)\).

Maximum spanning tree

Definition maximum spanning tree

Let \((G,w)\) be a weighted graph. A maximum spanning tree (of \((G,p)\)) is a graph \(G'\) such that

  1. \(G'\) is a spanning subgraph of \(G\);

  2. \(G'\) is a tree;

  3. the weight of \(G'\) is maximum among the weights of all the graphs satisfying condition 1 and condition 2 above, that is to say,

    • for any subgraph \(G''\) that is spanning for \(G\) and that is a tree, we have \(P(G') \geq P(G'')\).

We remark that the definition of a maximum spanning tree is similar to that of a minimum spanning tree, with two differences:

  1. the condition of connectedness is replaced by the stronger condition “to be a tree”;

  2. we consider the highest possible weight instead of the lowest weight.

The following property indicates that minimum and maximum spanning trees are equivalent up to an inversion of the weights of the edges (and more generally up to any decreasing function of the weights). This means that to obtain a maximum spanning tree, one can

  1. start by inverting the weights of the graph; and

  2. consider a minimum spanning tree in the graph with inverted weights.

Conversely, to obtain a minimum spanning tree, we can invert the weights of the graph and find a maximum spanning tree in the graph with inverted weights.s.

Property

Let \((G,w)\) be a weighted graph and let \(G'\) be a graph. The two following propositions are equivalent:

  • \(G'\) is a minimum spanning tree of \((G,w)\); and

  • \(G'\) is a maximum spanning tree of \((G, 1/p)\),

where, for each edge \(u\) of \(G\), we have \([1/p] (u) = 1 / (p(u))\).

Proof (as an exercise, for the curious).

Exo - Computing minimum spanning trees

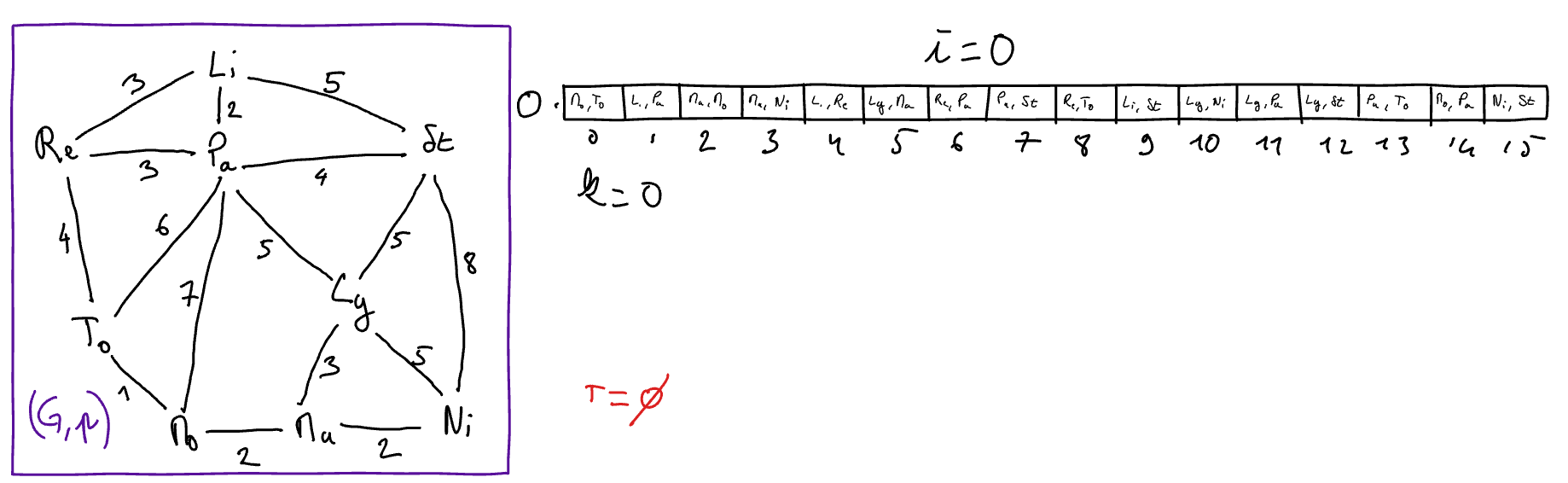
  1. Execute Kruskal’s algorithm “by hand” on the graph of the “toy example”. To this end, you will explain the state of the variables at each iteration of the main loop of the algorithm (hint: get inspired by the presentation in the course below).

  2. Indicate whether the suggestion that you made earlier (i.e. in the previous Exo section) for the spy network was correct.

  3. Implement Kruskal’s Algorithm. If you need help, all you need to do is

    • Download the new versions of source files graphes.h and graphes.c (which now contain data structures and functions to handle weighted graphs)

    • Fill in the code of the function algoKruskal in the file arbrePoidsMin.c (every annex function to sort the edges and to compute the connected components have been implemented for you :-) )

  4. Test your implementation of Kruskal’s algorithm on

  5. Use your implementations of Kruskal’s Algorithm and of Arborescence Algorithm seen in part 1 to print the list of “communications” to be established between the agents in order to broadcast the secret message from agent 007 while minimizing the probability that the message be intercepted.

Use

  • For each communication, you have to display the sender and the receiver of the message.

  • Include in your report a trace of the execution of your program.

Course - Kruskal’s Algorithm

There are several efficient algorithms for computing a minimum spanning tree from a weighted graph. Among the best known, we can cite:

We start by presenting a generic scheme (known as greedy) to obtain a minimum spanning tree before precisely describing Kruskal’s Algorithm which follows this generic principle. We then analyze the correctness and complexity of Kruskal’s Algorithm.

Generic scheme for computing minimum spanning trees

Kruskal’s algorithm progressively builds a minimum spanning tree

  • by adding edges one by one;

  • by starting from a graph which does not contain any edge.

The algorithm ends when the set of added edges forms a minimum spanning tree. If the graph \(G\) contains \(n\) vertices, the algorithm must therefore stop after adding \(n-1\) edges. The pseudo-language scheme of this generic algorithm is therefore as follows.

generic-MST Algorithm

Data: A weighted graph \((G,w)\) with \(n\) vertices and such that \(G=(V,E)\)

Result: A set \(T\) of edges such that the pair \((V,T)\) is a minimum spanning tree of \(G\)

  1. \(T := \emptyset\)

  2. \(k := 0\) // variable used to count the number of edges in T

  3. While \(k < n-1\) Do

    1. Select an edge \(u\) safe 1 for \(T\) and \((G,w)\)

    2. \(T := T \cup \{u\}\) // we add u to T

    3. \(k := k + 1\) // we update the value of the counter `k` of the number of edges in T

Notes

1

The notion of a safe edge used in this pseudo-code is defined right after.

Intuitively, when we are in the conditions of the algorithm, a safe edge is an edge which can be added to \(T\) to build a minimum spanning tree. In other words, if \(T\) is a “part” of a minimum spanning tree then \(T \cup \{u\}\) must also be a part of a minimum spanning tree, this part being a little larger since it contains an additional edge. The following definition formalizes the notion of a safe edge.

Definition: safe edge

  • Let \((G,w)\) be a weighted graph such that \(G=(V,E)\).

  • Let \(T\) be a subset of \(E\) such that \((V,T)\) is a subgraph of a minimum spanning tree of \((G,w)\).

  • Let \(u\) be an edge of \(G\) that does not belong to \(T\).

  • We say that the edge \(u\) is safe (for \(T\) en \(G\) ) if the graph \((V, T \cup \{u\} )\) is a subgraph of a minimum spanning tree of \((G,w)\).

From this definition, it can be observed that generic-MST Algorithm does indeed produce a minimum spanning tree. Indeed,

  • after initialization (line 1 and 2), the set \(T\) is empty, which implies that the pair \((V,T)\) is indeed a subgraph of a minimum spanning tree of \((G,w)\) ;

  • at each iteration of the While loop (line 3), we add a safe edge in \(T\), which implies that at each iteration the pair \((V,T)\) indeed remains a subgraph of a minimum spanning tree of \((G,w)\); and

  • when the algorithm ends the condition of the While loop is false, which implies that \(k\) is equal to \(n-1\) and therefore that \(T\) is a subgraph with \(n-1\) edges of a minimum spanning tree. As any minimum spanning tree is made of exactly \(n-1\) edges, we deduce that \(T\) is necessarily a minimum spanning tree when the algorithm halts.

In order to propose an algorithm which can be used in practice to compute a minimum spanning tree, it remains to propose an efficient means of detecting edges which are safe. This is precisely the subject of the next section.

Kruskal’s Algorithm

Kruskal’s algorithm is a particularization of generic-MST Algorithm. At each iteration, a safe edge is detected and added to the spanning tree under construction. To detect a safe edge, the idea is to find an edge of least possible weight among the edges that connect two distinct connected components of the partial minimum spanning tree which is under construction (denoted by \(T\)). To achieve this,

  • an array of the edges of the graph sorted in increasing order of weights is computed at the beginning of the algorithm; and

  • at each iteration, one searches in this array the edge of smallest index which links two distinct connected components of \(T\). We can observe that it is not necessary to go through the sorted array again from the beginning at each iteration. Indeed, it suffices to restart the search at the index of the previous edge added to \(T\) because the edges with lower indices have already been considered and are therefore either already in \(T\) , or are made up of two vertices belonging to the same connected component of \(T\).

The pseudo-language description of Kruskal’s algorithm is given below.

Kruskal’s Algorithm

Datas: A weighted graph \((G,w)\) with \(n\) vertices and \(m\) edges, such that \(G=(V,E)\)

Result: A set \(T\) of edges such that the pair \((V,T)\) is a minimum spanning tree of \((G,w)\)

  1. \(T := \emptyset\)

  2. \(k := 0\) // variable used to count the number of edges in T

  3. \(i := 0\) // variable used to browse the edges by increasing order of weights

  4. Sort the edges in \(E\) by increasing order of weights, that is

    • Compute the array \(O\) made of the \(m\) edges of \(G\) such that

      • \(E = \{O[0], \ldots, O[m-1]\}\) ; and

      • \(w(O[i]) \geq w(O[i-1])\) for any \(i\) in \(\{1, \ldots, m-1\}\)

  1. While \(k < n-1\) Do

    1. \(\{x,y\} = O[i]\) // select for x and y the extremities of the i-th edge in the sorted array

    2. If \(y\) does not belong to \(CC( (V,T) ,x)\) 2 Then // the edge {x,y} is safe

      1. \(T := T \cup \{\{x,y\}\}\)

      2. \(k := k+1\)

    1. \(i := i+1\)

Notes

2

We remind that \(CC((S,T), x)\) denotes the connected component of the graph \((V,T)\) that contains \(x\) and that this component can be obtained in linear time with ‘CC Algorithme.

Execution example (city graph)

Execution Algorithme de Kruskal (init) Execution Algorithme de Kruskal (0) Execution Algorithme de Kruskal (1) Execution Algorithme de Kruskal (2) Execution Algorithme de Kruskal (3) Execution Algorithme de Kruskal (4) Execution Algorithme de Kruskal (5) Execution Algorithme de Kruskal (6) Execution Algorithme de Kruskal (7) Execution Algorithme de Kruskal (8) Execution Algorithme de Kruskal (final)

Choix des structures de données et Analyse de complexité

To analyze the complexity of Kruskal’s algorithm, we will assume that:

Let us analyze the complexity of each line of Kruskal’s Algorithm.

  • Line 1 consists of initializing \(T\), this can be done in \(O(n)\) complexity (an empty list for each vertex of the graph)

  • Line 2 and 3 are in constant time complexity.

  • Line 4 consists of sorting \(m\) edges, which can be done with a standard sorting algorithm in \(O(n\log(n))\).

  • The continuation condition of the While loop (line 5) can be tested in constant time and it is tested at most \(m+1\) times during the execution. Indeed, in the worst case, the edge of highest weight (thus localized at index \(m-1\) in array \(O\)) belongs to the minimum spanning tree. It is therefore necessary to have traversed all the other edges of the graph before inserting it in \(T\). In this case, the body of the While loop is repeated \(m\) times and the test is executed once more. The complexity of Line 5 is therefore \(O(m)\).

  • Line 6 is executed at most \(m\) times (for the reasons given just before) and its complexity is then in \(O(m)\).

  • The test of line 7 is also repeated at most \(m\) times. To assess this test, it is necessary to find the connected component of \((V,T)\) containing \(x\). This operation is in \(O(|S| + |T|)\) when using CC algorithm. The number of edges in \(T\) is bounded by \(n-1\) since \(T\) is a tree at the end of the algorithm. Thus, the time complexity of Line 6 is \(O(mn)\).

  • Lines 7 and 8 are repeated at most \(n-1\) times (once for each edge inserted in \(T\)). The complexity of this lines is thus \(O(n)\).

  • Line 9 is repeated at most \(m\) times, its complexity is in \(O(m)\).

Overall, the complexity of Kruskal’s algorithm is therefore in \(O(m\log(m) + mn)\). This complexity can be reduced to \(O(m\log(m) + \alpha(n)n)\), where \(\alpha\) is an extremely-slow growing function (typically \(\alpha(n)\) is less than 5 when \(n\) is equal to the number of atoms in the universe), by using the Union-Find Algorithm of Robert Tarjan to dynamically handle the connected components of \(T\). Finally, it should be noted that in certain cases frequently encountered in practice, we can sort the edges in linear time (for instance when the weights take their values in a “small” subset of integers). In this case the time complexity of the algorithm is in \(O(mn)\), decreased to \(O(\alpha(n)n)\) by using Union-Find algorithm.

Proof of correctness of Kruskal’s Algorithm

To be included for a next iteration of the course graphs and algorithms :-) This proof relies on a “cut theorem” that formalizes the idea given in the beginning of the previous section.

To go further…

At ESIEE Paris, within the Laboratoire d’Informatique Gaspard Monge,, we contribute to the advancement of research on minimum spanning trees (and on Kruskal’s Algorithm) in the context of image analysis and artificial intelligence! To know more, you can for instance have a look at the following scientific articles that we wrote:

If you want to join our team, we can create with and for you E4 research projects, internships and consider a future PhD topic for the most passionate. Do not hesitate to contact us! We will talk with pleasure about our research work. We even launched a specific program in order to introduce you to research in E4 (and continuing in E5):