Discovering and exploring graphs: part 2

Common thread problem and rules of the game

Fil rouge

In the first part of this course we saw how we can model Parisian cycle paths with a graph. In this second part, we will see how to efficiently explore these cycle paths to discover the part of the Parisian map that is reachable from a given starting point. In other words, we will answer the original question:

  • Where can I cycle from home using cycle paths?

Because of the one-way cycle paths, it is quite possible that there are places in Paris that one can expect without being able to return home. We will then be interested in studying a second problem:

  • Where can I cycle to and back from my home?

In terms of graphs, this will lead us to focus on the following 3 fundamental concepts:

  • graph traversal (also known as graph search) and path;

  • connected component; and

  • strongly connected component.

We will also study efficient algorithms to extract these objects from a given graph and a starting vertex. Although we rely in this course on the particular example of cycle paths, the scope of application of these notions is much wider since they are necessary in a large part of the problems that can be solved with graphs (as, by example, those that we will see in the rest of this course: data partitioning, shortest paths, optimal-weight networks of ).

Organization of the course

Every section with a title labeled “Exo” refers to exercises related to the common thread problem.You must answer these questions in groups of 4 students and record your answers in a report. You must keep the same group as for the first part of the course. You have to

  • continue with the google document created previously;

  • share it with other group members; and

  • share it at the start of the session with the teacher.

or questions that require code, you will be asked to copy the code you produced into your report. For this type of questions, you will not be asked to write an entire program on your own but to complete a graph library written in C. Thus, you should never have to produce more than twenty lines of code per question.

The produced report will be used for your evaluation in the “Graphs and Algorithms” course.

In general, each section labeled “Exo” is followed by a section labeled “Course” which presents the concepts necessary to answer the questions related to the common thread problem.

In the flow of the course sections, you will also find small quizzes which aim to test your understanding of the course. To check your answers, all you have to do is click on the “correct” button at the end of the exercise.

This course is not a mooc! A teacher is here to help you: call hime whenever you have the slightest doubt or to check your answers. The teacher can also enter comments directly in your report. Take these remarks into account to improve your answers.

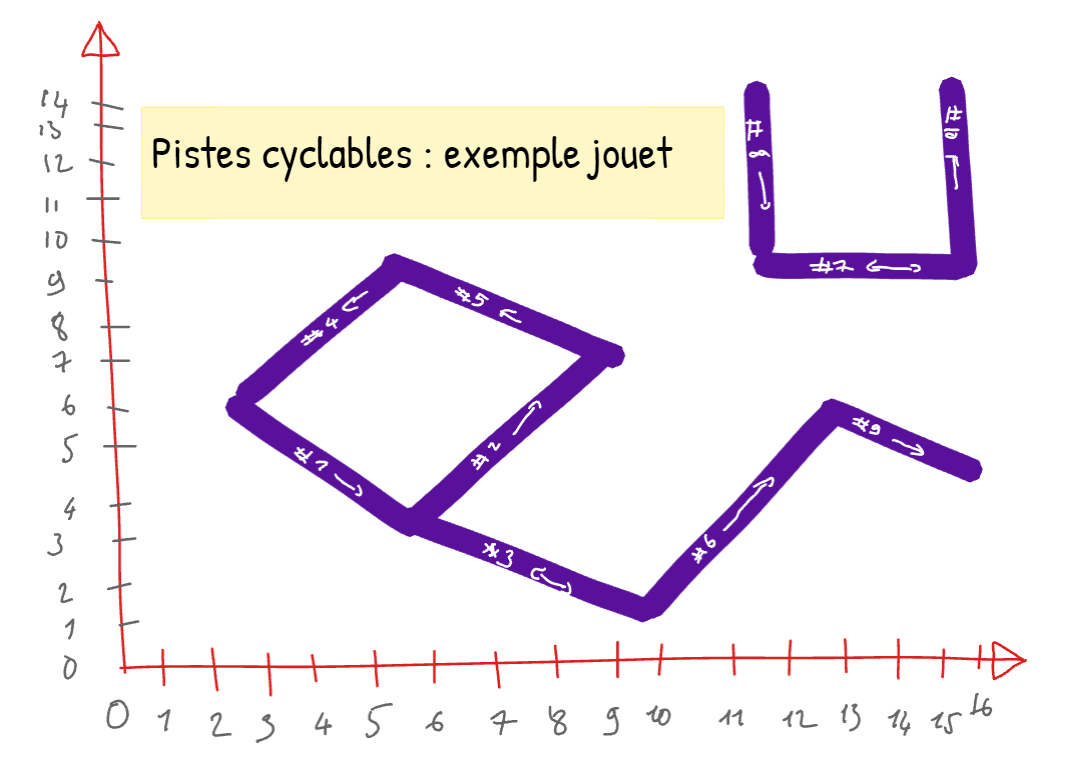
A “toy example”: reminder

Consider the following cycle paths identified by their ends in a Cartesian coordinate system:

  1. one way from (3;6) to (6;3)

  2. one way from (6;3) to (9;7)

  3. two-way between (6;3) and (10;1)

  4. one way from (6;9) to (3;6)

  5. one way from (9;7) to (6;9)

  6. one way from (10;1) to (13;6)

  7. two-way between (12;9) and (16;9)

  8. one way from (12;13) to (12;9)

  9. one way from (13;6) to (16;4)

  10. one way from (16:9) to (16;13)

Plan des pistes

Exo - Successor search: dilation algorithm

In the graph \(G = (V,A)\) that models the cycle paths of the toy example, consider the vertex \(x\) associated to the position \((3;6)\) as the starting point and give

  • the dilation \(E_1 = \delta(G,\{x\})\) of the set \(\{x\}\)

  • the dilation \(E_2 = \delta(G,E_1)\) of \(E_1\)

  • the dilation \(E_3 = \delta(G,E_2)\) of \(E_2\)

In the previous example, if we continue the dilation steps (that is to say, if we consider the seriese \(E_0, E_1, \ldots\) where \(E_i = \delta(G,E_{i-1})\) and \(E_0 = \{x\}\)), from which step do we no longer discover unexplored summits?

Complete the pseudo-code algorithm below to compute the dilation of a subset of vertices of a graph.

Dilation algorithm

Data: the number \(n\) of vertices of the graph \(G\), the successor map \(\Gamma\) of the graph \(G\), and a subset \(E\) of vertices of the graph

Results: the dilation \(D\) of \(E\) in \(G\)

  1. \(D := \emptyset\)

  2. For each \(x\) from \(0\) to \(n-1\) Do

    1. If \(x\) is in \(E\) Then

    1. Complete here!!

Assuming that the graph \(G\) is represented in memory by an array of linked lists, assess the complexity of the algorithm in the following two cases:

  1. each of the sets \(D\) and \(E\) is represented in memory by a linked list; and

  2. each of the sets \(D\) and \(E\) is represented in memory by a Boolean array.

In each case, you will assess the complexity of each row of the algorithm before assessing the overall complexity.

Now complete the following implementation of the Dilation algorithm.

#include "graphes.h"

/* ci-dessous trois macros pour pouvoir utiliser les termes, booleens, VRAI et FAUX dans les programmes */
#define booleen unsigned char
#define VRAI 1
#define FAUX 0

/***************************************************************************/
/* retourne le dilate D de l'ensemble E dans le graphe G                   */
/* les ensembles E et D sont représentés par des tableaux booleens         */
/* - la mémoire pour E est supposée allouée avec autant de case            */
/*   que de sommets dans G                                                 */
/* - la mémoire pour D est allouée a l'intérieur de la fonction            */
/***************************************************************************/
booleen * dilatation(graphe* G, booleen *E){
    booleen *D; /* tableau boolen pour stocker le résultat de la dilatation */
    int x; /* pour parcourir les sommets de G */
    pcell p; /* pointeur vers maillon pour parcourir des listes de successeurs */

    /* comme D est un sous ensemble des sommets de G on a besoin
    d'autant de cases que de sommets de G */
    D = (booleen *) calloc(G->nsom, sizeof(booleen));

    /* A completer ici, peut se faire en 4 lignes, en tout cas en au plus 7 :-) */

    return D;
}

In order to test your implementation of the dilation algorithm:

  • download the file exploration_dilatation.c and save it in your working directory

  • insert your own dilation code in this file at the place provided for it

  • compile the program (with gcc exploration_dilatation.c graphes.c -o exploration_dilatation or even better with make)

  • test it on several graphs (for example amitie.graphe, your toy-example graph, and pistes.petit.graphe 1 ) ;

  • check that the results are as expected; and

  • copy the execution traces of your programs to your report.

Notes

1(1,2,3)

Bonus : OObtain a graph visualization! To this end

  • download the source file graphe2ps and save it in your directory

  • compile it, for instance, with the command gcc graphe2ps.c graphes.c -o graphe2ps -lm

  • This program allows you to convert a graph in the form of a file .graphe into a graphical illustration in the form of a .eps file that can be visualized for instance a pdf viewer as evince.

Do not forget to include a visualization of (some) of your graphs in your report ;-) !

By executing the program of graph search by dilation (by hand or using “exploration_dilatation” on a machine), we can get convinced that, at step \(k\) of the algorithm, the vertices found are those that can be reached by “riding” through \(k\) cycle-path sections (i.e., \(k\) arcs) from the starting point.

Indicate (in natural language) a method to obtain the set of vertices of the graph from which we can reach a starting vertex by borrowing k arcs (help: you can combine several algorithms seen so far).

Course - Exploration of successors: dilation

Intuitively, in a graph, to browse over all the vertices that can be reached from a given initial vertex, we can proceed step by step by considering the successors of the initial vertex, then the successors of the successors, the successors of these successors, etc. In such a procedure, the elementary operation consists in exploring the successors of a subset of vertices. This operation is called a dilation.

Définition: Dilation

Let \(G = (V,A)\) be a graph and let \(E\) be a subset of vertices of \(G\). The dilation of \(E\) in \(G = (S,A)\), denoted by \(\delta(G,E)\), is the union of the sets of successors of the elements in \(E\) :

  • \(\delta(G,E) = \cup \{ \Gamma_G(x), x \in E \}\).

Example

Let \(G\) be the graph that is drawn below.

Example of a graph

  • The dilation of the set \(E = \{0, 3, 7\}\) in \(G\) is the set \(\delta(G,E) = \{1, 5, 4, 8\}\) since \(\Gamma_G(0) = \{1\}\), \(\Gamma_G(3) = \{5,4\}\), \(\Gamma_G(7) = \{8\}\), and \(\{1\} \cup \{5,4\} \cup \{8\} = \{1, 5, 4, 8\}\).

We can observe that a vertex \(x\) of \(G\) belongs to the dilation of \(E\) if and only if one of its predecessor belongs to \(E\). In other words, we can easily prove that the following statement holds true:

  • \(\delta(G,E) = \{ x \in S \text{ tel que } \exists (y,x) \in A \text{ wher } y \in E \}\).

Exo - Paths

In the graph \(G\) that models the data of the “toy-example” problem, give

  1. an elementary path of length 4;

  2. a non trivial circuit that is an elementary path;

  3. a non-trivial chain that is not a path;

  4. the length of a longest elementary path;

  5. a cycle that is not a circuit;

  6. a circuit that is not an elementary path;

  7. the set of vertices of the graph that can be reached by a path from the vertex at position \((12; 9)\) ;

  8. the set of vertices from which there exists a path leading to the vertex at position \((12; 9)\)

  9. the set made of each vertex that can both

    • be reached by a path from position \((12; 9)\); and

    • from which we can come back to the position \((12 ; 9)\) with a path;

  10. same work as in the previous item for position \((6;9)\) and then from position \((13;6)\).

Course - Paths

In order to study precisely the exploration of graphs, this section is devoted to the notion of a path. This notion plays an important role in graph search methods. Indeed, in a graph, a vertex can be “explored” from another if there is a path going from the second one to the first one.

Intuitively, in a graph, a path is an ordered series of vertices in which each element is linked by an arc to that which precedes it and to that which follows it.

Definition: Path

Let \(G = (V, A)\) be a graph, and let \(x\) and \(y\) be two vertices in \(S\).

A path from \(x\) to \(y\) (in \(G\)) is an ordered sequence \(\pi = (x_0, \ldots, x_\ell)\) of vertices in \(V\) such that

  • for any \(i\) in \(\{1, \ldots, \ell \}\), \(x_i\) is a successor of \(x_{i-1}\) in \(G\); and

  • \(x_0 = x\) and \(x_\ell = y\)

If \(\pi = (x_0, \ldots, x_\ell)\) is a path, we say that \(\ell\) is its length.

Example

In the graph \(G\) drawn below, \(\pi = (0,2,1)\) is a path of length 2.

Example of a graph

Some paths have remarkable characteristics and are then given a particular name.

Definition: Remarkable paths

Let \(G\) be a graph.

  • A zero-length path is calle a trivial path.

  • A non-trivial path \(\pi = (x_0, \ldots, x_\ell)\) is a circuit if its first and last vertices are equal, that is, if we have \(x_0 = x_\ell\).

  • A path \(\pi = (x_0, \ldots, x_\ell)\) is elementary if its vertices are pairwise disctinct except possibly \(x_0\) and \(x_\ell\), that is, is for any two \(i\) and \(j\) in \(\{0, \ldots, \ell\}\) with \(i \neq j\), we have \(x_i \neq x_j\) where \(\{i,j\} \neq \{0,\ell\}\).

Example

In the graph \(G\) drawn below,

  • \((3)\) is a trivial path;

  • \((0,2,1,0)\) is a circuit;

  • the circuit \((0,2,1,0)\) is elementary; and

  • \((0,1,0,2,1,0)\) is a circuit that not elementary.

Example of a graph

From the definition of an elementary path, we deduce the following property. Intuitively, this property allows us to assert that any vertex that can be reached from a given initial vertex can also be reached thanks to an elementary path of length less than the total number of vertices in the graph. We will use this property in a later section to show that a graph search algorithm is correct and efficient:

  • it indeed produces the set of all the vertices which can be reached from the initial vertex without missing a single one; and

  • it produces this result in a bonded number of steps.

Property

  • Any path \(\pi\) from \(x\) to \(y\) contains an elementary path from \(x\) to \(y\).

  • The length of an elementary circuit in \(G\) is at most equal to \(n\), \(n\) being the number of vertices in \(G\).

  • The length of an elementary path that is not a circuit is at most \(n-1\).

As seen with the example of rebel cycle bikers (those who only take one-way streets in the wrong direction), it is sometimes interesting not to consider the orientation of the arcs of a graph. In this case, it is relevant to consider the notions of chain and cycle instead of that of path and circuit.

Définition: Chain and circuits

Let \(G\) be a graph and let \(G_s\) be the symmetric closure of \(G\) 2

  • Any path in \(G_s\) is called a chain of \(G\).

  • Any elementary circuit in \(G_s\) with at least three vertices is called a cycle in \(G\).

Notes

2

See section Cours - Symmetric and Graphs for a reminder about the definition of symmetric closure

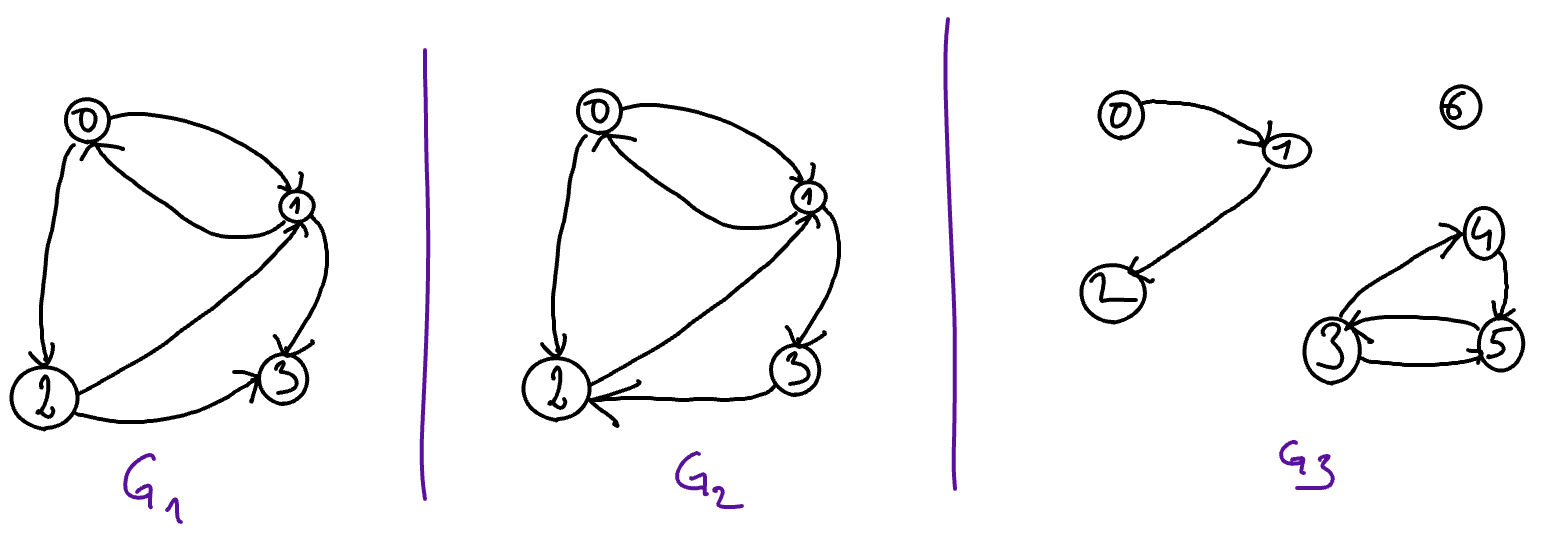
Consider the graph \(G\) drawn below and fill in the following table. In each box, indicate true (V) if you think that the sequence given at the beginning of the row satisfies the definition given at the top of the column.

Exemple d'un graphe

is a path

is a chain

is a circuit

is a cycle

\((0,2,0)\)

\((0,2,1,0,2,3)\)

\((3,2,0)\)

\((0,2,1,2,0)\)

\((2,0,1,2)\)

\((0,2,1,0)\)

Course - Partial search of a graph

In this section we will see that, given an initial vertex in a graph and a given length \(\ell\), it is possible to obtain the set of vertices reachable from this vertex by a path of length \(\ell\) by iterating \(\ell\) times the dilation algorithm studied in the previous section. We will then see that it is possible to obtain all the reachable vertices from the initial vertex by iterating a sufficient (but limited) number of times the dilation algorithm. This algorithm is in quadratic time. We will see in a next section how to improve it to obtain an algorithm in linear time with respect to the size of the graph in order to search for all the vertices that can be reached from a starting vertex

Intuitively, the search of rank \(k\) from a given starting vertex is the set of vertices that can be reached from this vertex by iterating \(k\) from the set comprising only the starting vertex.

Definition: Partial search :class: definition

Let \(G\) be a graph, let \(x\) be a vertex of \(G\), and let \(k\) be a positive integer. The (partial) search of rank \(k\) (of \(G\) ) from \(x\) is the subset of the vertices of \(G\) denoted by \(\Gamma_G^k(x)\) and defined by:

  • \(\Gamma_G^k(x) = \{x\}\), if \(k = 0\); and

  • \(\Gamma_G^k(x) = \delta(G,\Gamma_G^{k-1}(x))\), if \(k > 0\).

We can also observe that:

  • \(\Gamma_G^0(x) = \{x\}\) ;

  • \(\Gamma_G^1(x) = \delta(G,\Gamma_G^0(x)) = \delta(G,\{x\}) = \Gamma_G(x)\) ;

  • \(\Gamma_G^2(x) = \delta(G,\Gamma^1(x)) = \delta(G,\delta(G,\{x\}))\) ;

  • \(\Gamma_G^3(x) = \delta(G,\Gamma^2(x)) = \delta(G,\delta(G,\delta(G,{x})))\) ;

  • …

  • More generally, \(\Gamma_G^k(x) = \delta(G,\Gamma^{k-1}(x)) = \delta(G,\delta(G,...(\delta(G,\{x\})...))\), where the dilation is applied \(k\) times.

Example

Let \(G\) be the graph drawn below.

Example of a graph

  • We observe that

    • \(\Gamma_G^0(0) = \{0\}\) ;

    • \(\Gamma_G^1(0) = \{1\}\) ;

    • \(\Gamma_G^2(0) = \{2,6\}\) ;

    • \(\Gamma_G^3(0) = \{0,5\}\) ;

    • \(\Gamma_G^4(0) = \{1,4\}\) ;

    • \(\Gamma_G^5(0) = \{3, 6, 2\}\) ;

    • \(\Gamma_G^6(0) = \{4, 5, 0\}\).

We can now state the following property that establishes a formal link between searches of rank \(k\) and paths of length \(\ell = k\).

Property

  • Theres exists a path of length \(\ell\) from \(x\) to \(y\) if and only if \(y\) is in the search of rank \(k = \ell\) from \(x\)

Poof (for curious students).

  • We use induction to prove this property

    1. [Initiatilzatoin of the induction] Let us first establish the property when \(\ell = 0\). There exists a path of lenth \(\ell = 0\) from \(x\) to \(y\) if and only if \(y = x\) sinbce the only path of length \(0\) starting at \(x\) is the trivial path \((x)\). As the search \(\Gamma_G^0(x)\) of rank 0 from \(x\) is the set \(\{x\}\) (cf first item in the above definition), we deduce that the property is true when \(\ell = 0\).

    2. [Induction hypothesis] Let us now assume that \(\ell\) is (strictlyà positive and that the property holds tru at rank \(\ell -1\), that is to say that the follwing statement holds true:

      • there exists a path of length \(\ell-1\) from \(x\) to \(y\) if and only if \(y\) is in the search of rank \(\ell - 1\) from \(x\)

    3. [Induction] let us now prove that, under this assumption, the property also holds true at rank \(\ell\), which will complete the infuction proof. We will first prove the direct implication before establishing the backward one:

      • If \((x = x_0, \ldots, x_\ell=y)\) is a path of length \(\ell\) from \(x\) to \(y\), then, from the definition of a path, we may affirm that

          1. \(\pi' = (x_0, \ldots, x_{\ell - 1})\) is a path of lenth \(\ell -1\) from \(x\) to \(x_{\ell-1}\) and that

          1. \(y\) is a successor of \(x_{\ell-1}\).

      By induction hypothesis, we deduce from (a) that \(x_{\ell-1}\) is in the search \(\Gamma_G^{\ell-1}(x)\) of rank \(\ell-1\) from \(x\). Thus, from (b), by definition of \(\Gamma_G^{\ell}(x)\) (see the second item in the above definition), we deduce tha the vertex \(y\) is in the search \(\Gamma_G^{\ell}(x)\) of rank \(\ell\) from \(x\), which completes the proof of the forward implication.

      • If \(y\) is in the search \(\Gamma_G^{\ell}(x)\) of rank \(k = \ell\) from \(x\), then, from the definition of \(\Gamma_G^{\ell}(x)\) (see the second item in the above definition), we may affirm that there exists an element \(z\) in \(\Gamma_G^{\ell-1}(x)\) such that \(y\) is a successor of \(z\). Thus, from the induction hypothesis, there exists a path \((x_0, \ldots, x_{\ell -1} = z)\) of length \(\ell-1\) from \(x\) to \(z\). Hence, as \(y\) is a successor of \(z\), \((x_0, \ldots, x_{\ell -1}=z, x_{\ell} = y)\) is a path of length \(\ell\) from \(x\) to \(y\), which completes the proof of the backward implication.

    QED.

Exo - Coding graph search algorithms

  1. Naive graph search.

    1. Implement this algorithm by completing the code of ‘’explorationNaif’’in the source file explorationNaif.c

    2. Compile your program (gcc explorationNaif.c graphes.c -o exploration or better using make)

    3. Test your program with several graphs: amitie.graphe, your toy-eample graphe, and pistes.petit.graphe 1 )

    4. Verify that the results are correct

    5. Report the execution time for complete graph of cycle paths from vertex 1072 (AVENUE DES CHAMPS ELYSEES).

  2. Breadth-first search

    1. Implement this algorithm by completing the code of the function ‘’explorationLargeur’’ in the source file explorationLargeur.c

      • Hint: Use the list structure that was implemented for you. This structure mmust be handled exclusively with the five given functions: ‘’initListFIFO’’, ‘’termineListFIFO’’, ‘’selectionSuppressionListeFIFO’’, ‘’insertionListeFIFO’’ et ‘’estNonVideListeFIFO’’.

    2. Compile your program (gcc exploration.c graphes.c -o exploration or even better using make)

    3. Test your program with several graphs: amitie.graphe, your toy-eample graphe, and pistes.petit.graphe 1 )

    4. Verify that the results are correct

    5. Report the execution time for complete graph of cycle paths from vertex 1072 (AVENUE DES CHAMPS ELYSEES).

  3. Tell in each of these two cases (partial and complete gra^h of cycle paths) if it is possible to bike anywhere in the (partial) graph of the Parisian cycle pathsfrom the given starting points.

Course - Graph search algorithm

Course - Naive graph search algorithm

We can now present a first algorithm to compute the search in a graph. This algorithm consists of

  1. successively obtain each partial search of order \(k\), for every \(k\) from 0 eto \(n\) (set \(D\) below); and

  2. save, at each step, the union of previous partial explorations (set \(Z\) below).

Thus, according to the previous property, at the end of the algorithm the result obtained is indeed the exploration of the graph from the given initial vertex.

Naive graph search algorithm

Data: the number \(n\) of vertices of the graph \(G\), the successor map \(\Gamma\) of \(G\), and a vertex \(x\) of \(G\)

Résult: the search \(Z = \mbox{Expl}(G,x)\) from \(x\)

  1. \(E := \{x\}\); \(D := \emptyset\); \(Z := \{x\}\)

  2. For each \(k\) from \(1\) to \(n-1\) Do

    1. \(D := \delta(G,E)\) // use the algorithm seen in the exercise Exo - Exploration … dilatation

    2. \(Z := Z \cup D\)

    3. \(E := D\)

We will analyze the computational complexity of this algorithm assuming that the different subsets of vertices (\(E,D\), and \(Z\)) are represented by Boolean arrays and that the graph is represented by an array of successor lists. To this end, we analyze the time complexity of each of its lines.

  1. Line 1 consists of initializing \(E, D\) and \(Z\) represented by three Boolean arrayx. Its complexity is then \(\mathcal{O}(n)\).

  2. Line 2 is trivialy in \(\mathcal{O}(n)\) .

  3. Line 3 consists of executin the dilation algorithm at each iteration of the For each loop (\(n-1\) iterations). The time-complexity of the dilation algorithl being \(\mathcal{O}(n+m)\), the complexity of Line 3 us then \(\mathcal{O}(n(n+m))\).

  4. Line 4 consists of computing the union of two subsets of vertices at each iteration of the For each loop (\(n-1\) iterations). The two sets being represented by Boolean arrays, each union step can be performed in \(\mathcal{O}(n)\). As we need to perform \(n-1\) unions, the overall complexity of Line 4is \(\mathcal{O}(n^2)\).

  5. Line 5 consists of assigning, at each iteration of the For each loop (\(n-1\) iterations), the set \(D\), resulting from the dilatoin, to the variable \(E\). Such assignement can be done in constant time (address handling) an thus the overall complexity of Line 5is \(\mathcal{O}(n)\).

Thus, we deduce the following property that esablishes the time complexity of Naive seach algorithm.

Complexity of Naive search

When the graph is represented as an array of linked lists, and when the subsets of verices are represented by Boolean arrays, the complexity of Naive search algorithm is

  • \(\mathcal{O}(n(n+m))\),

where \(n\) and \(m\) are the numbers of vertices and of graphs, respectively, of the given graph \(G\).

Course - Breadth-first search algorithm

In this section, we present one of the most famous graph search algorithm, namely breadth-first search algorithm.

This algorithm can be obtained by improving the naive algorithm. To this end, two improvements can be made to the naive graph search algorithm in order to reduce the time complexity of Lines 3 and 4.

  1. The first improvement consists, during the execution of the dilation algorithm, of “blocking” the search from a vertex already considered during a previous iteration, that is to say, if the vertex is already in the set \(Z\) (and thus if it belongs to a partial search of rank strictly lower than the current value of the variable \(k\)). Indeed, the search from this blocked vertex is not necessary since it has already been considered in a previous iteration. Thus, we reduce the number of operations without changing the content of the set \(Z\) of explored vertices.

  2. The second improvement consists of inserting directly in \(Z\) the elements found during the dilation step in order to suppress the union operations performed at Ligne 4.

Breadth-first search algorithm is presented below. It can be seen in particular that the two lines 3 and 4 of the naive algorithm have been replaced here by lines 3 to 8 which allows for integrating the two improvements presented above.

Breadth-First Search Algorithm (version 1)

Data: the number \(n\) of verices in the graph \(G\), the successor map \(\Gamma\) of the graph \(G\) and a vertex \(x\) of the graph \(G\)

Result: the search \(Z = \mbox{Expl}(G,x)\) from \(x\)

  1. \(E := \{x\}\); \(D := \emptyset\); \(Z := \{x\}\)

  2. For each \(k\) from \(1\) to \(n-1\) Do

    1. While \(E \neq \emptyset\) Do

      1. \(y :=\) an arbitrary element of \(E\) ; \(E := E \setminus \{y\}\) // Selection-deletion

      2. For each \(z\) in \(\Gamma(y)\) Do

        1. If \(z\) is not in \(Z\) Then

          1. \(D := D \cup \{z\}\)

          2. \(Z := Z \cup \{z\}\)

    1. \(E := D\) ; \(D := \emptyset\)

Let us now analyze the time complexity of Breadth-First Search algorithm. In this analysis, we assume that

  • the successor map of the graph \(G\) is represented by an array of linked lists;

  • the sets \(E\) and \(D\) are represented by lists; and

  • the set \(Z\) is represented by a Boolean array.

At line 1, the initializations of \(E\) and of \(D\) can be done in \(\mathcal{O}(1)\) (since these sets are represented by lists) wheras the initialization of \(Z\) (represented by a Boolean array) has a \(\mathcal{O}(n)\) complexity. The complexity of Line 2 is trivialy \(\mathcal{O}(n)\).

In order to analyze the complexity of the next lines of the algorithms, we need to state the following obervations:

  • each vertex of \(G\) is inserted at most once in \(D\). Indeed, each time an element is inserted in \(D\) (line 7), it is also inserted in \(Z\) (Line 8) and, before every insertion of an element \(z\) in \(D\), we first make sure that this element \(z\) is not already in \(Z\) (Line 6). As we never suppress any element from \(Z\), we deduce that each vertex of the graph is inserted at most once in \(D\);

  • each vertex of \(G\) is inserted at most once in \(E\). Indeed, the only instruction to append an element to \(E\) is the one at Line 9 that consists of transferring in \(E\) the elements from \(D\). Thus, as each vertex is inserted at most once in \(D\) (see previous observation), we deduce that each vertex of \(G\) is inserted at most once in \(E\).

At each iteration of the while loop, element is removed from \(E\). As every vertex of \(G\) is inserted at most once in \(E\), the test of the while loop returns true at most \(n\) times. We also observe that this test returns false \(n-1\) times (1 negative test per iteration of the while loop). Thus, the time complexity of Line 3 is \(\mathcal{O}(n)\).

The instruction at Line 4 is executed at most \(n\) times (once for each positive test of the while loop) and each execution of this instruction (selection-deletion) is in \(\mathcal{O}(1)\) since \(E\) is represented by a Boolean array.

The complexity of Line 5 is \(O(n+m)\), \(m\) being the number of arcs of \(G\). Indeed, in the worst case, each vertex of the graph is selected and deleted once from \(E\). Hence, the list of successor of each vertex is browsed at most once at Line 5, leading to a \(O(n+m)\) complexity (if necessary, review the complexity analysis of SYM algorithm ).

Searching an element in a set represented as a Boolean array being a constant time operation and Line 6 being executed at most \(m\) times, we deduce that the complexity of Line 6 is \(\mathcal{O}(m)\). The (external) insertion of an element in a set being a constant time operation, Lines 7 and 8 are also in \(\mathcal{O}(m)\).

Finaly, the instructions of Line 9 can be don by swapping the adresses of \(E\) and \(D\). Thus, the complexity of this line is \(\mathcal{0}(n)\).

We therefore deduce the following property that establishes the linear time complexity of Breadth-First Search Algorithm.

Complexity of Breadth-First Search Algorithm.

When the graph is represented by an array of linked lists, when the subsets \(E\) and \(D\) are represented by lists and when the set \(Z\) is represented by a Boolean array, the complexity of Breadth-First Search Algorithm is

  • \(\mathcal{O}(n+m)\),

where \(n\) and \(m\) are the numbers of vertices and of arcs, respectively, of the given graph \(G\).

Breadth-First Search Algorithm wan be rewritten with less instruction lines. To this end, we insert the element in \(E\) directly instead of passing them through the set \(D\). This rewriting, presented hereafter, does not change the time complexity of the algorithm nor its complexity when the set \(E\) is implemented with a FIFO list (First In - First-Out).

Breadth-First Search ALgorithm (version 2)

Data: the number \(n\) of verices in the graph \(G\), the successor map \(\Gamma\) of the graph \(G\) and a vertex \(x\) of the graph \(G\)

Result: the search \(Z = \mbox{Expl}(G,x)\) from \(x\)

  1. \(E := \{x\}\); \(Z := \{x\}\)

  2. While \(E \neq \emptyset\) Do

    1. \(y :=\) the first element in \(E\) ; \(E := E \setminus \{y\}\) // selection-deletion

    2. For each \(z\) in \(\Gamma(y)\) Do

      1. If \(z\) is not in \(Z\) Then

        1. \(E := E \cup \{z\}\)

        2. \(Z := Z \cup \{z\}\)

Exo - Connectivity

  1. G ive for each vertex \(x\) of the toy-example graph:

    • the connected component containing \(x\); and

    • the strongly connected component containing \(x\).

  2. Using the terminology of graph theory, explain what is the set of locations where we can cycle to and back from home.

  3. Same question if one is allowed to use one-way tracks in the wrong direction.

Course - Connectivity

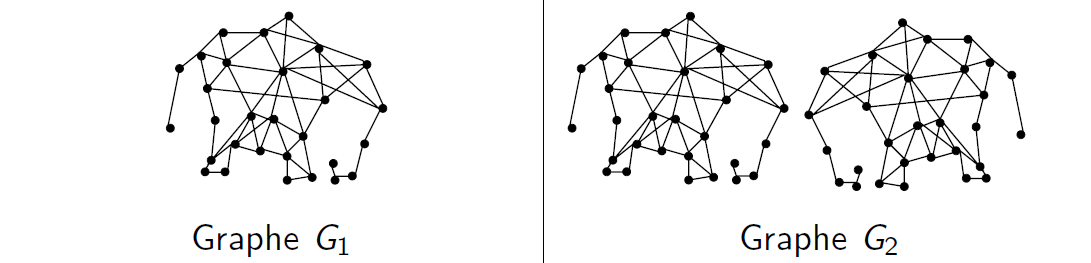
In this section we will focus on the notion of connectivity in graphs. This topological notion plays an important role in many applications or fundamental fields ranging from visual perception (Gestalt theory) to data analysis or geography and topography. For example, if we ask ourselves the question of describing the differences between the two images below, we will readily answer that:

  • picture 1 is all in one piece, it contains a single piece / object (the elephant) and that

  • picture 2 includes two pieces, it contains two objects (two elephants).

Some elephants

Connectivity in graphs allows one to formalize this notion of “in one piece” and to identify the different “pieces” of a graph. In this section, we will study, using paths, the notions of connected and of strongly connected components of a graph. We will then present, using Breadth-First Search Algorithm, an efficient algorithm to compute the connected and strongly connected components containing a given vertex of a graph.

Connectivity (and strong connectivity)

Intuitively, a graph is connected if there is a path allowing one to go from any vertex to any other. For example, this characteristic can be checked in the graph \(G_1\), depicted below, but not in \(G_2\): we say that \(G_1\) is connected but that \(G_2\) is not. When the graphs are directed, we can distinguish between two different notions depending whether or not we want to consider the orientations of the arcs.

Elephants as graphs

Definition

Let \(G\) be a graph.

  • The graph \(G = (V,A)\) is connected if, for every two vertices \(x\) and \(y\), there exists a chain 3 from \(x\) to \(y\).

  • The graph \(G = (V,A)\) is strongly connected if, for any two vertices \(x\) and \(y\), there exists a path 3 from \(x\) to \(y\)

Notes

3(1,2)

We observe that the only difference between the notions of connected graph and of strongly connected graph lies in the difference between path and chain, that is to say if the orientations of the arcs is taken into account or not. As any chain is a path, we can also observe that any strongly connected graph is also necessarily connected.

Let \(G_1\), \(G_2\), and \(G_3\) be the thre graphs depicted below. For each of them, indicate in the following table if it is connected or not.

Trois graphes

is connected

is strongly connected

\(G_1\)

\(G_2\)

\(G_3\)

Connected components (and strongly connected components)

We have seen in the previous section how to define if a graph is connected or not. In this section, we study the subparts of a graph which are connected (or strongly connected) and which are as large as possible to satisfy this property of connectedness (i.e. maximal for inclusion).

Definition : connected component

Let \(G =(V,A)\) be a graph and let \(x\) be a vertex of \(G\)

The connected component of \(G\) containing \(x\), denoted by \(\mbox{CC}(G,x)\), is the subset of \(V\) which contains every element that can be reached from \(x\) by a chain:

\[\begin{eqnarray} \mbox{CC}(G,x) = \{ y \in V \text{ such that there exists a chain from } x \text{ to } y \} . \end{eqnarray}\]

Example

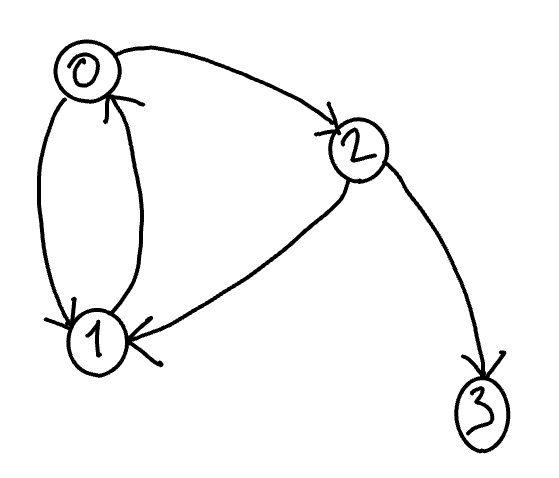
Let \(G\) be the following graph.

Exemple d'un graphe

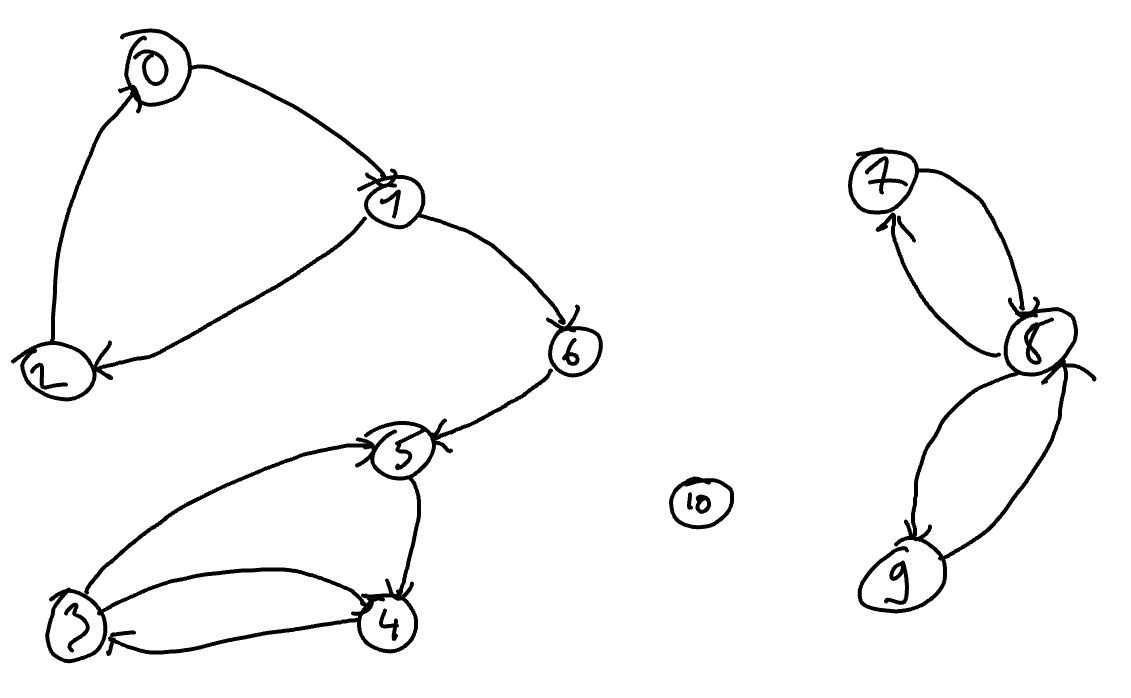
We observe that there is a chain from vertex 0 to vertices 0, 1, 2, 6, 5, 4, and 3 but not from 0 to 7, 8, 9, nor 10. We can thus affirm that the connected component containing vertex 0 is the set \(\{0, 1, 2, 6, 5, 4,3\}\) :

  • \(\mbox{C}(G,0) = \{0, 1, 2, 6, 5, 4,3\}\).

We also oberve that:

  • \(\mbox{CC}(G,0) = \mbox{CC}(G,1) = \mbox{CC}(G,2)= \mbox{CC}(G,3)= \mbox{CC}(G,4)= \mbox{CC}(G,5)= \mbox{CC}(G,6)= \mbox{CC}(G,1) = \{0, 1, 2, 6, 5, 4,3\}\) ;

  • \(\mbox{CC}(G,10) = \{10\}\) ; and

  • \(\mbox{CC}(G,7) = \mbox{CC}(G,8) = \mbox{CC}(G,9) = \{7,8,9\}\).

Let \(G_3\) be the following graph.

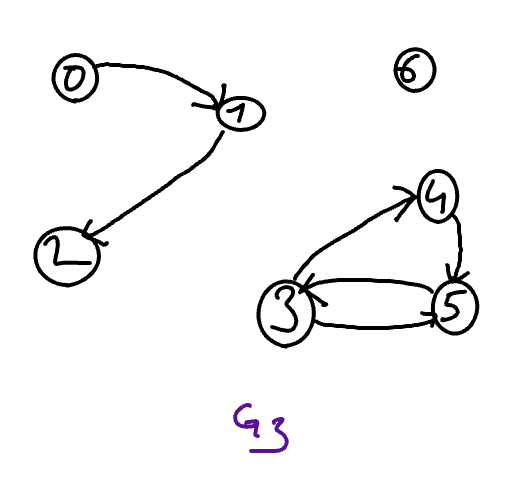
Un graphe

Complete the following table with True (V) or False (F) by indicating for each pair of vertices \(x\) and \(y\) if the second one (\(y\)) is in the connected component containing the first one (\(x\)).

\(\mbox{CC}(G,0)\)

\(\mbox{CC}(G,1)\)

\(\mbox{CC}(G,2)\)

\(\mbox{CC}(G,3)\)

\(\mbox{CC}(G,4)\)

\(\mbox{CC}(G,5)\)

\(\mbox{CC}(G,6)\)

\(0 \in\)

\(1 \in\)

\(2 \in\)

\(3 \in\)

\(4 \in\)

\(5 \in\)

\(6 \in\)

Definition: strongly connected component

Let \(G =(V,A)\) be a graph and let \(x\) be a vertex of \(G\)

The strongly connected component of \(G\) containing \(x\), denoted by \(\mbox{SCC}(G,x)\), is the subset of \(V\) that contains each vertex that can be reached from \(x\) and from which \(x\) can be reached back by a path :

\[\begin{eqnarray} \mbox{SCC}(G,x) = \{ y \in S \text{ such that there is a path from } x \text{ to } y \text{ and there is a path from } y \text{ to } x \} . \end{eqnarray}\]

Example

Let \(G\) be the following graph.

Example of a graph

From the drawing, we can make the following observations:

  1. there is a path from vertex 0 to vertex 1 and there is a path from vertex 1 to vertex 0: vertex 1 is therefore in the strongly connected component containing vertex 0;

  2. there is no path from vertex 0 to vertex 10: vertex 10 does not belong to the strongly connected component of vertex 0; and

  3. there is a path from vertex 0 to vertex 6 but there is no path from vertex 6 to vertex 0: vertex 10 does not belong to the strongly connected component of vertex 0.

We also observe that:

  • \(\mbox{SCC}(G,0) = \mbox{SCC}(G,1) = \mbox{SCC}(G,2)= \{0, 1, 2\}\) ;

  • \(\mbox{SCC}(G,6) = \{6\}\) ;

  • \(\mbox{SCC}(G,3) = \mbox{SCC}(G,4) = \mbox{SCC}(G,5) = \{3, 4, 5\}\) ;

  • \(\mbox{SCC}(G,7) = \mbox{SCC}(G,8) = \mbox{SCC}(G,9) = \{7, 8, 9\}\) ;

  • \(\mbox{SCC}(G,10) = \{10\}\) ;

Let \(G_3\) be the graph drawn below.

Un graphe

Complete the following table with True (V) or False (F) by indicating for each pair of vertices \(x\) and \(y\) if the second one (\(y\)) is in the stronly connected component containing the first one (\(x\)).

\(\mbox{SCC}(G,0)\)

\(\mbox{SCC}(G,1)\)

\(\mbox{SCC}(G,2)\)

\(\mbox{SCC}(G,3)\)

\(\mbox{SCC}(G,4)\)

\(\mbox{SCC}(G,5)\)

\(\mbox{SCC}(G,6)\)

\(0 \in\)

\(1 \in\)

\(2 \in\)

\(3 \in\)

\(4 \in\)

\(5 \in\)

\(6 \in\)

A remarkable property of connected and strongly connected components

For the curious students

In this section, we establish an important structural property of connected and of strongly connected components. A major consequence of this property is that a graph can be “split” into connected (and strongly connected) components.

Property

Let \(G = (V,A)\) be a graph. The relation “is in the connected component containing” is an equivalence relation, that is to say that the three follwoing statements hold true:

  1. [reflexivity] for any vertex \(x\) in \(G\), \(x\) is in \(CC(G,x)\)

  2. [symmetry] for any two vertices \(x, y\) in \(G\), if \(y\) is in \(CC(G,x)\), then \(x\) is in \(CC(G,y)\); and

  3. [transitivity] for any three vertices \(x, y, z\) in \(G\), if \(y\) is in \(CC(G,x)\) and \(z\) is in \(CC(G,y)\), then, \(z\) is in \(CC(G,x)\).

Proof

  1. As \((x)\) is a chain, from the definition of a connected component, \(x\) is in \(CC(G,x)\).

  2. Assume that \(y\) is in \(CC(G,x)\). Then, there exists a chain \(\pi = (x_0 = x, \ldots, x_\ell=y)\) from \(x\) to \(y\) (definition of \(CC(G,x)\)), that is, \(\pi\) is a path from \(x\) to \(y\) in the symmetric closure \(G_s\) of \(G\) (definition of a chain). As \(G_s\) is a symmetric graph,, \(\pi' = (x_\ell = y, \ldots, x_0=x)\) is also a path in \(G_s\) and, hence, \(\pi'\) is a chain from \(y\) to \(x\), which means that \(x\) is in \(CC(G,y)\).

  3. Assume that \(y\) is in \(CC(G,x)\) and that \(z\) is in \(CC(G,y)\). Then, there exists a chain \(\pi =(x=x_0, \ldots, x_\ell=y)\) from \(x\) to \(y\) and a chain \(\pi' =(y=y_0, \ldots, y_k=z)\) from \(y\) to \(z\). Then, we can observe that the series \(\pi'' =(x=x_0, \ldots, x_\ell=y=y_0, \ldots, y_k=z)\) is a chain, which implies that \(z\) is in \(CC(G,x)\). QED

Corollary

Let \(G = (V,A)\) be a graph. The set of connected compoents of \(G\) is a partition of \(S\) :

  • for any pair \((x,y)\) of vertices in \(G\), either \(CC(G,x) = CC(G,y)\) or \(CC(G,x) \cap CC(G,y) = \emptyset\).

Proof (by contradiction) As an exercise ;-)

Property

Let \(G = (V,A)\) be a graph. The relation “is in the strongly connected component containing” is an equivalence relation, that is to say that the three follwoing statements hold true:

  1. [reflexivity] for any vertex \(x\) in \(G\), \(x\) is in \(SCC(G,x)\)

  2. [symmetry] for any two vertices \(x, y\) in \(G\), if \(y\) is in \(SCC(G,x)\), then \(x\) is in \(SCC(G,y)\); and

  3. [transitivity] for any three vertices \(x, y, z\) in \(G\), if \(y\) is in \(SCC(G,x)\) and \(z\) is in \(SCC(G,y)\), then, \(z\) is in \(SCC(G,x)\).

Preuve

  1. As \((x)\) is a path, from the definition of a strongly connected component \(x\) is in \(CC(G,x)\).

  2. Assume that \(y\) is in \(SCC(G,x)\). By definition of a strongly connected component, there exists a path \(\pi = (x_0 = x, \ldots, x_\ell=y)\) from \(x\) to \(y\) and a path \(\pi' = (y_0 = y, \ldots, y_k=x)\) from \(y\) to \(x\) (definition of \(SCC(G,x)\)). Thus, from the definition of a strongly connected component, \(x\) is in \(SCC(G,y)\).

  3. Assume that \(y\) is in \(SCC(G,x)\) and that \(z\) is in \(SCC(G,y)\). Then, there exists

  • a path \(\pi_1 =(x=x_0, \ldots, x_\ell=y)\) from \(x\) to \(y\);

  • a path \(\pi'_1 =(y=y_0, \ldots, y_k=x)\) from \(y\) to \(x\);

  • a path \(\pi_2 =(y=w_0, \ldots, w_i=z)\) from \(y\) to \(z\); and

  • a path \(\pi'_2 =(z=z_0, \ldots, z_j=y)\) from \(z\) to \(y\).

We observe that the sequence \(\pi =(x=x_0, \ldots, x_\ell=y=w_0, \ldots, w_i=z)\) is a path from \(x\) to \(z\) and that the sequence \(\pi =(z=z_0, \ldots, z_j=y=y_0, \ldots, y_k=x)\) is a path from \(z\) to \(x\), which implies that \(z\) is in \(SCC(G,x)\). WED

Corollary

Let \(G = (V,A)\) be a graph. The set of strongly connected components of \(G\) is a partition of \(S\):

  • for any pair \((x,y)\) of vertices in \(G\), either \(SCC(G,x) = SCC(G,y)\) or \(SCC(G,x) \cap SCC(G,y) = \emptyset\).

Proof (by contradiction) To be done as an exercise ;-)

Exo - Coding connected component algorithm

  1. Implement SCC algorithm.

    • Hint #1: start by copying the source file of the program explorationLargeur

    • Hint #2 : copy the code of the function symEfficace that is in your source file symetrique.c

  2. Using your program, list all the “places” where we can bike to and come back

  3. [Optional] Same work as above but considering that we allow one to use one-way track in the opposite direction.

Course - Connected Component and Strongly Connected Component Algorithms

In this section, we present two algorithms. Given a graph and a vertex of this graph,

  • the CC algorithm computes in linear time the connected component containing this vertex; and

  • the SCC algorithm computes the strongly connected component containing this vertex.

These two algorithms use, in the form of a function call, the two algorithms studied in previous sections to compute symmetric and graph search. In order to establish the correctness of these calls, we start by establishing a property that characterizes connected and strongly connected components using only the notions of search and of symmetric. Then, we directly derive the two algorithms CC and SCC from this property and study their time complexity.

Property

let \(G\) be a graph, let \(G^{-1}\) be the symmetric of \(G\), and let \(G_{s}\) be the symmetric closure of \(G\). Let \(x\) be a vertex of \(G\). Then, the two following equalities hold true:

  1. \(\mbox{CC}(G,x) = \mbox{Expl}(G_s,x)\)

  2. \(\mbox{SCC}(G,x) = \mbox{Expl}(G,x) \cap \mbox{Expl}(G^{-1},x)\)

Proof

  1. Since a chain is a path \(G_s\) and since \(\mbox{Expl}(G_s,x)\) is the set of all vertices that can be reached from \(x\) with a path \(G_s\), we deduce that :\(\mbox{Expl}(G_s,x)\) contains every vertex which can be reached from \(x\) by a chain, that is to say, from the definition of a connected component,that :\(\mbox{Expl}(G_s,x)\) is precisely the connected component containing \(x\).

  2. In order to justify the second equality, we remark, from the definition of the symmetric of a graph, that the following statement holds true:

    • there exists a path from \(y\) to \(x\) in \(G\) if and only if there exists a path from \(x\) to \(y\) in the symmetric \(G^{-1}\) of \(G\).

Hence, any vertex \(y\) that belong to both the search in \(G\) from \(x\) and the search in \(G^{-1}\) from \(x\) is a vertex that can be reached from \(x\) by a path in \(G\) and from which \(x\) can be reached by a path in \(G\), whic completes the proof of the second equality. QED

We now present the two algorithms, called CC and SCC, which are directly derived from the previous property. The previous property therefore allows us to guarantee that at the end of the execution of these algorithms, the computed results are indeed the connected component and the strongly connected component containing the given initial vertex.

CC Algorithm

Data: the number \(n\) of vertices in the graph \(G\), the successor map \(\Gamma\) of the graph \(G\), and a vertex \(x\) of the graph \(G\)

Result: the connected component \(Z = \mbox{Expl}(G,x)\) containing \(x\)

  1. Get the symmetric \(G^{-1}\) of \(G\) using SYM Algorithm

  2. Build the graph \(G_s\) from \(G\) and \(G^{-1}\)

  3. Compute \(\mbox{Expl}(G_s,x)\) with Bread First Search Algorithm and save the result in \(Z\)

If the graph is represented by an array of linked list, the time complexity of Lines 1 and 3 is \(\mathcal{O}(n+m)\). Line 2 can also be performed in linear tim by adding the arcs of \(G_s\) by successively browsing the successor lists of \(G\) and of \(G^{-1}\). Thus, we deduce the following property that establishes the time complexity of CC Algorithm.

Complexity of CC Algorithm

When the graph is represented by an array of linked lists, the time complexity of CC algorithm is

  • \(\mathcal{O}(n+m)\),

where \(n\) and \(m\) are the numbers of vertices and of arcs, respectively, of the given graph \(G\).

SCC Algorithm

Data: the number \(n\) of vertices in the graph \(G\), the successor map \(\Gamma\) of the graph \(G\), and a vertex \(x\) of the graph \(G\)

Result: the strongly connected component \(Z = \mbox{Expl}(G,x)\) containing \(x\)

  1. Compute \(\mbox{Expl}(G,x)\) thanks to Breadth-First Search Algorithm and store the result in \(X\)

  2. Get the symmetric \(G^{-1}\) of \(G\) using SYM Algorithm

  3. Compute \(\mbox{Expl}(G^{-1}, x)\) thanks to Breadth-First Search Algorithm and store the result in \(Y\)

  4. \(Z := \emptyset\)

  5. For each \(x\) from \(0\) to \(n\) Do

    1. If \(x\) is in \(X\) and \(x\) is in \(Y\) Then

      1. \(Z := Z \cup \{x\}\)

In the previous algorithm, if the graph is represented by an array of linked lists, based on the complexity analyzes of SYM and Breadth-Firest Search Algorithms, we deduce that the complexity of Lines 1 to 3 is \(\mathcal{O}(n+m)\). If the set \(Z\) is represented by a Boolean array, the complexity of Lines 4 and 5 is \(\mathcal{O}(n)\). Since (i) the set resulting from Breadth-Firest Search Algorithms is represented by a Boolean array and since (ii) the search for an element in a set with this representation can be done in constant time, we deduce that the complexity of Line 6 is linear (at most 2n searches in constant time). Finally, as inserting an element into the set \(Z\) can be performed in constant time (\(Z\) being represented by a Boolean array), we deduce that the complexity of Line 7 is also \(\mathcal{O}(n)\).. Therefor, we deduce the following property which establishes that the time complexity of SCC algorithm is linear.

Complexity of SCC Algorithm

When the graph is represented by an array of linked lists, the time complexity of SCC algorithm is

  • \(\mathcal{O}(n+m)\),

where \(n\) and \(m\) are the numbers of vertices and of arcs, respectively, of the given graph \(G\).