Opérateurs connexes
Les exercices à réaliser sont situés dans la base de code que vous récupérez en vous inscrivant sur le lien GitHub classroom reçu par mail [1]. Lisez bien le readme du dépôt pour comprendre comment l’utiliser. La majorité des fonctions demandées existent déjà dans OpenCV : le but n’est pas d’utiliser les fonctions d’OpenCV mais de les coder vous même ! Nous utiliserons donc uniquement les conteneurs de base d’OpenCV et les fontions d’entrée/sortie.
Important
Au cours de ce chapitre, vous compléterez le fichier ``tpConnectedComponent.cpp`` que vous devrez pousser sur votre dépôt git avant la prochaine séance (cf. consignes détaillées envoyées par mail).
Adjacence
Dans le premier chapitre nous avons vu les traitements d’histogramme qui modifient une image sans considération pour les aspects spatiaux : la façon dont la valeur d’un pixel est modifiée ne dépend pas de sa position dans l’image. Dans ce deuxième chapitre nous nous intéresserons aux relations de voisinnage entre les pixels et aux traitements qui exploitent principalement cette information.
Une image digitale peut être vue comme une grille de pixels carrés à coordonnées entières dans \(\mathbb{Z}^2\), on parle de pavage, dans laquelle un pixel peut avoir 4 ou 8 pixels voisins :
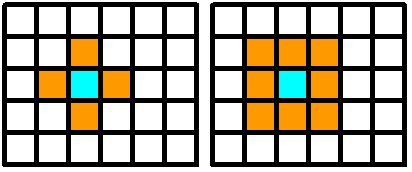
Grille des pixels. A gauche, représentation du 4-voisinnage : le pixel bleu est voisin des 4 pixels jaunes situés à gauche, à droite, au dessus et en dessous. A droite, représentation du 8-voisinnage : le pixel bleu est voisin des 8 pixels jaunes qui l’entourent (les 4 directions précendentes plus les diagonales).
On peut formaliser ces relations de voisinnage en définissant l’ensemble des pixels voisins d’un point de coordonnées \(p=(x,y)\in\mathbb{Z}^2\). L’ensemble des 4-voisins de \(p\), noté \(N_4(p)\) est donné par :
De manière similaire, l’ensemble des 8-voisins de \(p\), noté \(N_8(p)\) est donné par :
Ceci conduit en fait à définir deux graphes, le graphe de 4-adjacence et le graphe de 8-adjacence :
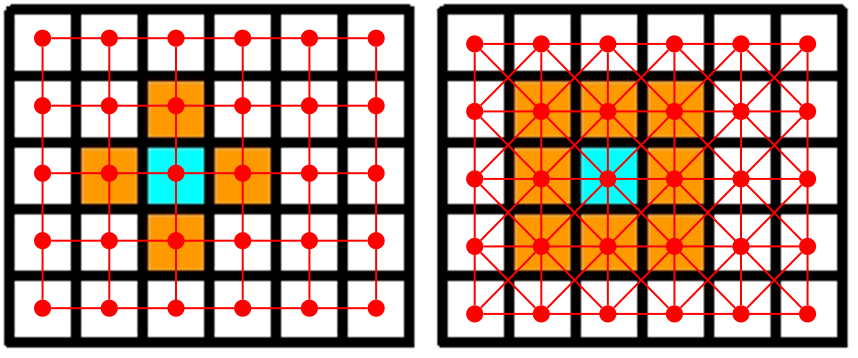
Chaque pixel représente un noeud du graphe, les arrêtes sont données par les relations d’adjacence \(N_4\) à gauche et \(N_8\) à droite.
Ce modèle permet de réutiliser les algorithmes de graphes (plus court chemin, composantes connexes, arbre couvrant de poids minimum…) pour analyser et traiter les images.
Composantes connexes
Un chemin \(A_{pq}\) d’un pixel \(p\) à un pixel \(q\) est une séquence de pixels \((x_1,\ldots,x_n)\) telle que :
\(p\) et \(q\) sont le départ et l’arrivée de \(A_{pq}\) : \(x_1=p\) et \(x_n=q\)
2 points consécutifs de \(A_{pq}\) sont voisins : \(\forall i=1,\ldots,n-1, \ x_{i+1}\in N(x_i)\)
Un ensemble de pixels \(X\) est dit connexe si, pour toute paire de pixels \(\{p, q\}\) dans \(X\), il existe un chemin de \(p\) à \(q\) dont tous les pixels sont contenus dans \(X\).
Une composante connexe d’un ensemble de pixels \(X\) est un sous ensemble \(Y\subseteq X\) tel que:
\(Y\) est connexe,
\(Y\) est maximal pour la connexité : si on ajoute un pixel de \(X\) à \(Y\) alors ce dernier n’est plus connexe.
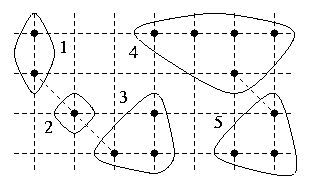
Exemple d’une image binaire, dont les pixels sont représentés par des ronds noirs. En 4-connexité, cette image comporte 5 composantes connexes. En 8-connexité, les composantes 1-2-3 et 4-5 fusionnent ne laissant que 2 composantes connexes.
L’algorithme fondamental qui nous intéressera par la suite est le parcours de composantes connexes. Il prend en entrée:
une image binaire : l’image à traiter,
un pixel \(p\) de l’image : la composante connexe contenant ce pixel sera parcourue,
une procédure prenant un pixel en paramètre : cette procédure sera appelée une fois sur chaque pixel de la composante connexe parcourue.
Il existe plusieurs variantes de cet algorithme, en voilà une qui effectue un parcours en profondeur au moyen d’une pile :
def parcoursCC(image im, pixel p, callback c):
pour tout pixel r de im:
visiter(r) <- faux
Pile s
s.empiler(p)
Tant que s n'est pas vide:
point r = s.pop()
c(r)
pour tout voisin v de r:
si v est dans im et visiter(v) est faux:
visiter(v) <- vrai
s.empiler(v)
Cet algorithme s’exécute en temps linéaire \(\mathcal{O}(n)\) (avec \(n\) le nombre pixels dans l’image) :
la condition sur
visiter(v)garantit qu’un pixel ne peut pas être mis plusieurs fois dans la pile : le nombre d’itérations de la boucletant queexterne est donc borné par le nombre pixels,le nombre d’itérations sur la boucle
pour toutinterne est constant (4 ou 8 selon l’adjacence choisie),dans le pire cas, la composante connexe s’étend sur toute l’image obligeant à visiter tous les pixels de l’image.
Astuce
Parcourir les voisins d’un pixels est une opération courante en traitement d’image. Une solution élégante est d’encoder la relation de voisinnage sous forme d’une liste de points avec des coordonnées relatives:
vector<Point2i> neighbours = {{-1,0}, {0,-1}, {0,1}, {1,0}};
Point2i pixel = {24, 12}; // coordonnées d'un pixel
//parcours des voisins de p
for(Point2i neighbour: neighbours)
{
neighbour += pixel;
}
Astuce
Une image binaire peut-être vue comme une fonction dans \(\{0,1\}\) ou comme un ensemble. D’un point de vue algorithmique/mathématique, la vision ensembliste est souvent plus simple (les ensembles sont des objets plus simples que les fonctions).
Sous OpenCV, les images sont représentées par des tableaux (donc des fonctions) et le type binaires n’est pas supporté (les opérations bits à bits ne sont pas efficaces sur les ordinateurs modernes). Les images binaires sont alors généralement représentées comme des images à niveaux de gris et on considère qu’un pixel de valeur non nulle est présent dans l’image.
Labélisation
L’étiquetage en composantes connexes ou labélisation consiste à parcourir une image binaire en assignant un numéro à chaque composante connexe de l’image. Le résultat de l’étiquetage est une nouvelle image, de même dimension que l’image binaire d’entrée, et dont la valeur d’un pixel est égale au numéro de la composante connexe auquel il appartient.
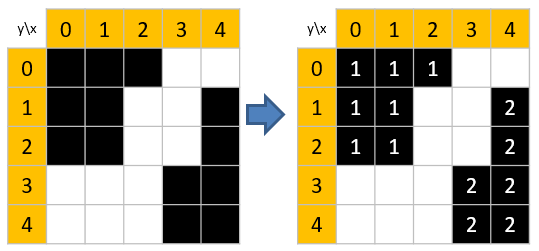
A gauche une image binaire composée de 2 composantes connexes (en noir). A droite : résultat de l’étiquetage en composantes connexes de l’image de gauche.

A gauche une image binaire (pixels blancs). A droite : résultat de l’étiquetage en composantes connexes de l’image de gauche: afin de faciliter la visualisation, une couleur aléatoire a été assignée à chaque composante connexe au lieu d’un numéro.
Adaptez l’algorithme parcoursCC pour implémenter l’étiquetage en composantes connexes (avec la 4-adjacence) dans la fonction ccLabel du fichier tpConnectedComponents.cpp. Pensez à valider votre implémentation avec la commande test.
Le filtre d’aire est un opérateur qui supprime toute les composantes connexes d’une image dont la taille (mesurée par le nombre de pixels dans la composante) est strictement inférieure à un seuil donné.
Implémentez un filtre d’aire dans la fonction ccAreaFilter (avec la 4-adjacence) du fichier tpConnectedComponents.cpp. Pensez à valider votre implémentation avec la commande test.
La fonction de labélisation implémentée précédemment réalise une exploration en profondeur (ou en largeur) des composantes connexes de l’image. Cette approche a une complexité linéaire, ce qui est optimal d’un point de vue théorique. En pratique cet algorithme a néanmoins le désavantage de réaliser des accès aléatoires en mémoire qui pénalisent ses performances (la mémoire cache est sous utilisée et les défauts de page sont fréquents).
Il existe un autre algorithme de labélisation en composantes connexes qui traite l’image en 2 passes (les pixels sont parcourus deux fois, ligne par ligne) qui a donc l’avantage de parcourir la mémoire dans l’ordre, ce qui lui permet d’être plus performant pratique. Implémentez l’algorithme de labélisation en 2 passes dans la fonction ccTwoPassLabel dans le fichier tpConnectedComponents.cpp.