Traitement d’histogramme

Les exercices à réaliser sont situés dans la base de code que vous récupérez en vous inscrivant sur le lien GitHub classroom reçu par mail [1]. Lisez bien le readme du dépôt pour comprendre comment l’utiliser. La majorité des fonctions demandées existent déjà dans OpenCV : le but n’est pas d’utiliser les fonctions d’OpenCV mais de les coder vous même ! Nous utiliserons donc uniquement les conteneurs de base d’OpenCV et les fontions d’entrée/sortie.

Important

Au cours de ce chapitre, vous compléterez le fichier ``tpHistogram.cpp`` que vous devrez pousser sur votre dépôt git avant la prochaine séance (cf. consignes détaillées envoyées par mail).

Notion d’histogramme

L’histogramme d’une image mesure la distribution des niveaux de gris dans l’image. Pour un niveau de gris x, l’histogramme permet de connaitre la probabilité de tomber sur un pixel de valeur x en tirant un pixel au hasard dans l’image.

Concrètement, l’histogramme d’une image à valeurs entières est construit de la manière suivante: pour chaque niveau de gris x, on compte le nombre de pixels ayant la valeur x.

Par exemple, soit l’image de 5 pixels par 5 pixels de côté avec des valeurs comprises entre 0 et 4 :

0

1

2

2

3

0

1

2

2

3

0

1

2

2

4

0

1

2

2

4

0

1

2

2

4

Son histogramme est une fonction qui, à chaque valeur de niveau de gris compris entre 0 et 4, associe le nombre de pixels ayant cette valeur:

Valeur de niveau de gris

0

1

2

3

4

Nombre de pixels

5

5

10

2

3

Ou bien, sous forme de diagramme baton :

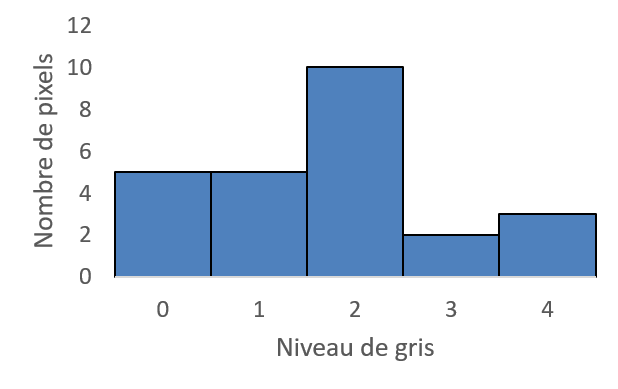
../_images/histoDemo.png

En divisant chaque valeur de l’histogramme par le nombre total de pixels dans l’image on obtient un histogramme normalisé. L’histogramme normalisé correspond à une distribution de probabilité empirique (toutes les valeurs sont comprises entre 0 et 1 et la somme des valeurs vaut 1).

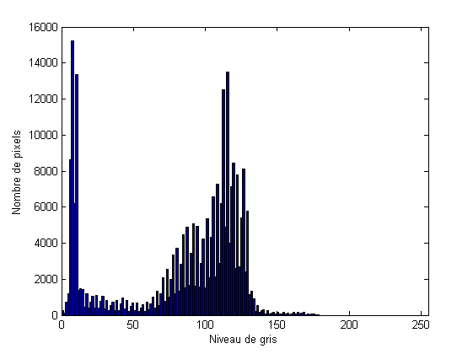
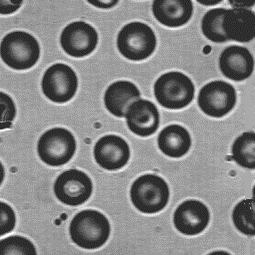
L’histogramme permet d’obtenir rapidement une information générale sur l’apparence de l’image. Une image visuellement plaisante aura généralement un histogramme équilibré (proche d’une fonction plate). Par exemple dans l’image ci-dessous, l’histogramme est tassé sur la gauche; l’image est trop sombre :

cam1 cam1H

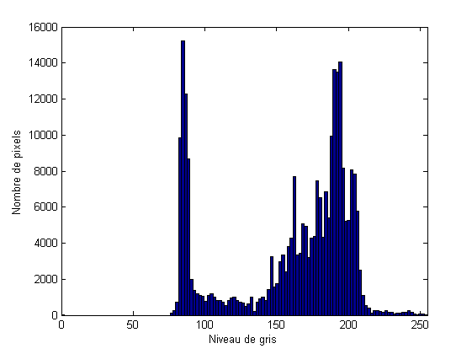
Maintenant, l’histogramme est tassé au centre; l’image est grisatre et manque de contraste :

cam2 cam2H

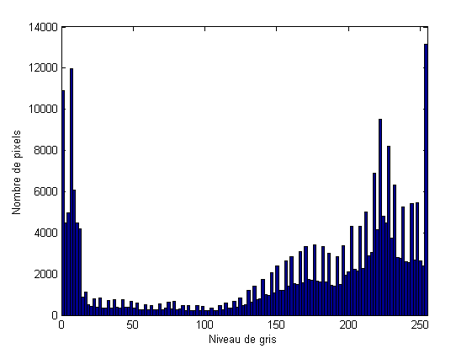
Finalement dans ce dernier exemple, l’histogramme est trop creusé au centre; les noirs sont trop noirs, les blancs trop blancs (on dit que l’image est saturée) :

cam3 cam3H

L’histogramme ne contient aucune information spatiale et des images très différentes peuvent avoir des histogrammes similaires. Par exemple les deux images ci-dessous :

adv1 adv2

ont le même histogramme:

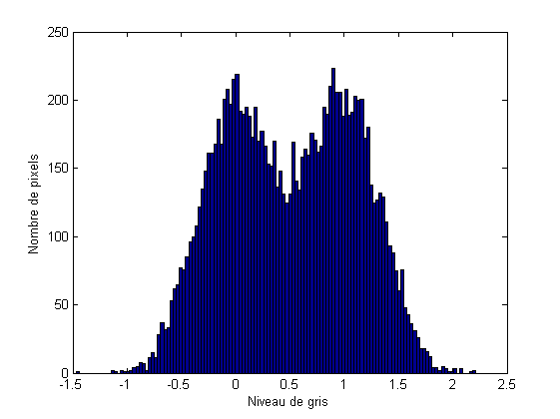
../_images/adverserialHisto.png

Formellement, pour une image \(f:E\rightarrow [0..n]\subseteq\mathbb{N}\), avec \(E\) l’ensemble des pixels, l’histogramme de \(f\) est une fonction \(T_f:[0,n]\rightarrow \mathbb{N}\) qui, à chaque niveau de gris \(v\), associe le nombre d’éléments \(x\) de \(E\) tel que \(f(x)=v\) :

\[T_f(v)=|\{x\in E; \ f(x)=v\}|\]

Transformation d’histogramme

En traitement d’image, les transformations d’histogramme modifient les images en traitant chaque pixel indépendamment. Ces transformations sont les plus simples, elles apparaissent dans presque tous les processus de traitement et d’analyse d’images : en pré-traitement pour normaliser l’image, ou en post-traitement pour améliorer la visualisation.

Etant données une image \(f : E \rightarrow V\), avec \(E\) l’ensemble des pixels et \(V\) l’espace des valeurs, et une fonction \(t : V \rightarrow V\). On définit \(f_t\) l’image \(f\) transformée par \(t\), comme la composition \(t \circ f\), c’est-à-dire :

\[\forall x\in E, f_t(x) = t(f(x))\]

Dans les logiciels de traitement d’images type Photoshop ou Gimp, la fonction \(t\) est généralement représentée par une courbe de transfert, manipulable à la souris:

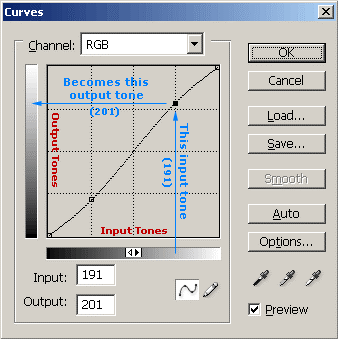
../_images/courbe_transfert.png

La fonction \(t\) est représentée par la courbe noire, on a donc sur l’axe du bas les valeurs de niveau de gris avant transformation et la courbe donne la valeur après transformation (axe des ordonnées).

Pour connaitre l’histogramme d’une image après transformation, il suffit d’appliquer la transformation à l’histogramme de l’image d’origine : l’hsitogramme ne contient pas d’information spatial et la transformation d’histogramme n’utilise aucune information spatiale.

Inversion et Introduction à OpenCV

Sous OpenCV, une image est représentée par la classe Mat (pour Matrix). Comme le nom le suggère, il s’agit d’un tableau à 2 dimensions. La mémoire des objets de type Mat est gérée automatiquement avec des smart pointer : vous n’aurez normalement pas à vous en soucier. Le type des éléments stockés dans une image est indiqué par une constante de la forme CV_8UC3 qui se lit 8 bit Unsigned Channel 3 (CV_ est juste un raccourci pour OpenCV…) : donc une image couleur (3 canneaux RGB) dont les valeurs sont de type unsigned char ([0, 255]).

Important

Dans la suite on utilisera essentiellement deux types d’images :

  • CV_32FC1 ou plus simplement CV_32F : les images en niveaux de gris (1 cannal) codées en nombre flottant. Dans ce cas la convention est d’avoir les valeurs des pixels comprises entre 0 (noir) et 1 (blanc)

  • CV_8UC1 ou plus simplement CV_8U : les images en niveaux de gris (1 cannal) codées sur 1 octet non signé ([0, 255]). Dans ce cas il faudra faire attention aux dépassements de capacités (255 + 1 == 0 sur 1 octet…)

Sauf mention contraire, le type par défaut sera CV_32FC1 ; les valeurs des pixels seront stockés dans des float.

Il existe de nombreuses façons de créer des objets de type Mat, notamment :

int height = 12;
int width = 21;
Mat image = Mat::zeros(height, width, CV_32FC1); // image initialisée à zéro de taille 12x21 avec des valeurs en float
Mat copie = image.clone(); // copie d'une image existante
Mat image2 = Mat::ones(height, width, CV_8UC1); // image initialisée à 1 de taille 12x21 avec des valeurs en uchar

L’accès aux éléments d’une image peut se faire en récupérant un pointeur sur les données brutes ou avec la fonction générique at qui retourne une référence sur un pixel :

image.at<float>(3,2) = 7; // modifie la valeur à la position: ligne 3, colonne 2
float v = image.at<float>(0,0); // lit la valeur à la position (0,0);

uchar v2 = = image2.at<uchar>(0,0); // si les valeurs sont codées sur 1 octet non signé

La taille d’une image peut être connue avec les champs cols (nombre de colonnes, donc largeur de l’image) et rows (nombre de lignes, donc hauteur de l’image):

int total = 0;
for(int y = 0; y < image.rows; y++)
        for(int x = 0; x < image.cols; x++)
                total += image2.at<uchar>(y, x);

La classe Mat permet de vectoriser certaines opérations par surcharge des opérateurs de base, ce qui permet d’éviter d’écrire des boucles for:

image = image + copie; // réalise l'addition des 2 images (somme matricielle)
image += 3; // ajoute la valeur 3 à la valeur de chaque pixel de l'image.

On souhaite définir une fonction d’inversion des niveau de gris donnée par la transformation \(inv\) définie par \(\forall x\in E, inv(x)=1-x\) (les blancs deviennent noirs et inversement).

../_images/cameracinv.png

Image du cameraman à gauche et image inversée à droite.

  1. Dans le projet situé sur le bureau de la machine virtuelle. Complétez la fonction inverse du fichier tpHistogram.cpp. Cette fonction prend en entrée une image \(f\) et doit retourner une nouvelle image \(f_{inv}\).

  2. Exécutez la commande make à la racine du projet pour compiler. Un exécutable appelé inverse est généré dans le dossier bin.

  3. Exécutez la commande ./inverse --help pour voir les options possibles. Ceci fonctionnera avec tous les exécutables générés dans les TPs.

  4. Exécutez la commande ./inverse -S pour exécuter la commande avec l’option -S pour afficher le résultat. Ceci fonctionnera avec tous les exécutables générés dans les TPs.

  5. Exécutez la commande ./test -P inverse -S pour effectuer un test unitaire sur votre programme. En cas de problème, le programme affiche la carte des différences par rapport au résultat attendu. Ceci fonctionnera avec tous les exécutables générés dans les TPs.

Seuillage

Soit une image \(f : E \rightarrow V\), la valeur maximale (respectivement minimale) de l’ensemble \(V\) est notée \(V_{max}\) (respectivement \(V_{min}\)). Par exemple dans le cas d’une image codée sur 8 bits non signé, on a \(V_{min}=0\) et \(V_{max}=255\). Un pixel ayant la valeur \(V_{min}\) ou \(V_{max}\) est dit saturé car sa valeur ne peut plus être augmentée (ou diminuée). Le seuillage est une opération qui consiste à saturer les pixels clairs (seuillage haut) ou sombres (seuillage bas) d’une image tout en laissant les autres inchangés.

Contrètement, dans le cas du seuillage haut, on se donne une valeur de seuil \(t\) dans \(V\), et la fonction de transformation \(sh_t : V \rightarrow V\) est définie ainsi :

\[\begin{split}\forall x \in V, sh_t(x)=\begin{cases}x \textrm{ si } x\leq t \\ V_{max} \textrm{ sinon}.\end{cases}\end{split}\]

Par exemple, l’image de gauche ci-dessous est une image hématologique sur laquelle ont voit des cellules sanguines. L’image de droite montre un seuil haut réalisé sur cette image : les pixels gris clairs sont maintenant blancs; les pixels plus sombres n’ont pas été modifiés.

blood bloodsh

Le seuillage bas est défini de manière symmétrique, on se donne une valeur de seuil \(t\) dans \(V\), et la fonction de transformation \(sb_t : V \rightarrow V\) est définie ainsi :

\[\begin{split}\forall x \in V, sb_t(x)=\begin{cases}x \textrm{ si } x>t \\ V_{min} \textrm{ sinon}.\end{cases}\end{split}\]

L’exemple ci-dessous montre un exemple de seuil bas : les pixels sombres sont maintenant noirs; les pixels clairs n’ont pas été modifiés.

blood bloodsb

Finalement, on peut également définir un seuillage combiné, on se donne une valeur de seuil bas \(tb\) et une valeur de seuil haut \(th\) dans \(V\), et la fonction de transformation \(s_t : V \rightarrow V\) est définie ainsi :

\[\begin{split}\forall x \in V, sb_t(x)=\begin{cases}V_{min} \textrm{ si } x \leq tb \\ x \textrm{ si } tb < x \leq th \\ V_{max} \textrm{ sinon}.\end{cases}\end{split}\]

L’exemple ci-dessous montre un exemple de seuil combiné reprenant les effets des deux exemples ci-dessus.

blood bloodsc

Le cas particulier d’un seuillage combiné où \(tb=th\) produit une image ne contenant que les valeurs \(V_{min}\) et \(V_{max}\): on parle d’image binaire et la transformation est une binarisation.

Complétez la fonction threshold du fichier tpHistogram.cpp qui réalise un seuillage combiné de l’image d’entrée.

Pensez à valider votre programme avec la commande ./test -P threshold -S pour effectuer un test unitaire sur votre programme.

Normalisation d’histogramme

Normaliser l’histogramme d’une image \(f\) consiste à appliquer une transformation d’histogramme à l’image afin d’étendre la plage de valeur de \(f\) à l’ensemble des valeurs disponibles. Concrètement, si l’on note \(f_{min}\) et \(f_{max}\) la valeur minimale et la valeur maximale de l’image, on souhaite trouver une transformation \(norm\) telle que \(norm(f_{min}) = V_{min}\) (\(V_{min}\) étant la valeur minimale que l’on souhaite atteindre) et \(norm(f_{max}) = V_{max}\) (\(V_{max}\) étant la valeur maximale que l’on souhaite atteindre). Cela n’est pas suffisant pour déterminer \(norm\), le modèle le plus simple est celui d’une fonction affine, c’est-à-fire une fonction de la forme \(ax+b\) qui trace une droite passant par les points de coordonnées \((f_{min},V_{min})\) et \((f_{max},V_{max})\).

Cela donne :

\[\forall x \in E, norm(x) = (x-f_{min})\frac{V_{max}-V_{min}}{f_{max}-f_{min}} + V_{min}\]

On peut facilement vérifier que \(norm(f_{min}) = V_{min}\), \(norm(f_{max}) = V_{max}\) et \(norm\) est une fonction affine (on peut l’exprimer sous la forme \(norm(x)=ax+b\)). L’image ci-dessous présente un exemple de normalisation d’image.

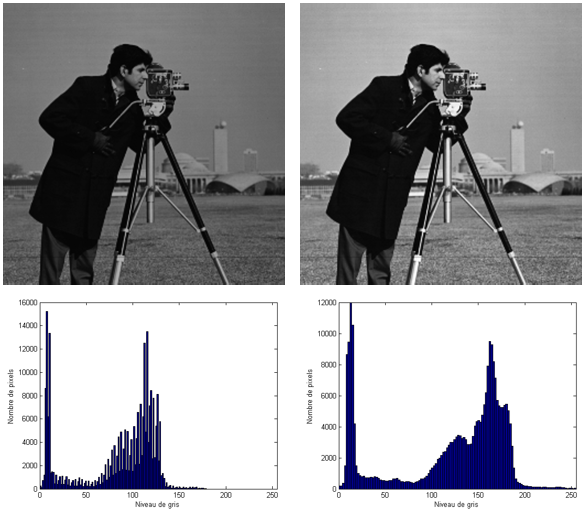
../_images/normalize.png

A gauche: image non normalisée qui n’atteind pas la valeur maximale possible dans les claires. A droite, image après normalisation : la plage de valeur s’étend sur tout l’intervalle disponible.

Attention

normalisation est un terme utilisé dans de nombreux contextes avec des sens souvent proches mais quand même… différents !

Implémentez cette transformation dans la fonction normalize du fichier tpHistogram.cpp. Pensez à valider votre implémentation avec la commande test.

Quantification

Le seuillage combiné permet de réduire le nombre de niveaux de gris à 2 dans une image à partir d’un niveau de seuil. L’opération plus générale qui consiste à réduire le nombre de niveaux de gris à \(k\) valeurs \(\{0,\ldots,k-1\}\) est appelée quantification. Le cas le plus simple est celui de la quantification uniforme. Dans ce cas, on commence par découper l’intervalle \([V_{min}, V_{max}]\) en \(k\) intervalles \(\{I_0,\ldots,I_{k-1}\}\) de longueurs uniformes. La quantification assigne alors à un pixel de valeur \(x\), le numéro de l’intervalle qui contient \(x\). Finalement, on se remet dans l’intervalle \([V_{min}, V_{max}]\).

Par exemple, pour quantifier une image prenant ses valeurs dans l’intervalle \([0,1]\) sur 3 valeurs, la transformation à appliquer est:

\[\begin{split}\forall x\in[0,1], q_3(x) = \begin{cases} 0 \textrm{ si } x <1/3 \\ 0.5 \textrm{ si } 1/3 \leq x < 2/3 \\ 1 \textrm{ sinon.}\\ \end{cases}\end{split}\]
../_images/quantif.png

Image de Lenna à différents de niveau de quantification (nombre de niveau de gris indiqué sous chaque figure).

Déterminez la fonction de transformation correspondant à la quantification uniforme sur \(k\) niveaux. Implémentez cette transformation dans la fonction quantize du fichier tpHistogram.cpp. Pensez à valider votre implémentation avec la commande test.

Egalisation d’histogramme

L’opération de normalisation d’histogramme permet d’étendre la plage de valeurs d’une image en étalant de manière uniforme les niveaux de gris de l’image sur tout l’intervalle de valeurs disponibles. Afin d’améliorer la qualité visuelle de l’image on peut chercher une transformation plus complexe (non uniforme) en partant du principe qu’une image avec un histogramme plat est généralement agréable. Concrètement, au lieu de chercher une transformation affine, on cherche une transformation croissante (on veut préserver l’ordre des niveaux des gris) telle que l’histogramme de l’image transformée soit le plus proche possible d’une distribution uniforme.

Afin de définir cette transformation, nous avons besoin de la notion d’histogramme cumulé qui mesure la distribution cumulée des niveaux de gris dans une image. Pour un niveau de gris \(x\), l’histogramme cumulé permet de connaitre la probabilité de tomber sur un pixel de valeur inférieure ou égale à \(x\) en tirant un pixel au hasard dans l’image.

L’histogramme cumulé d’une image \(f:E\rightarrow [0..n]\subset \mathbb{N}\), noté \(C_f\) est finalement donné par :

\[\begin{split}\begin{align} \forall v\in [0,n], C_f(v) & = |\{p \in E; f(p) \leq v \}| \\ &= \sum_{i=0}^{v} T_f(i) \end{align}\end{split}\]

L’histogramme cumulé se calcule donc simplement à partir de l’histogramme.

Par exemple, soit l’image de 5 pixels par 5 pixels de côté avec des valeurs comprises entre 0 et 4:

0

1

2

2

3

0

1

2

2

3

0

1

2

2

4

0

1

2

2

4

0

1

2

2

4

On obtient l’histogramme et l’histogramme cumulé :

Valeur de niveau de gris

0

1

2

3

4

Nombre de pixels

5

5

10

2

3

Histogramme cumulé

5

10

20

22

25

Où bien sous forme d’une courbe (avec l’histogramme en baton):

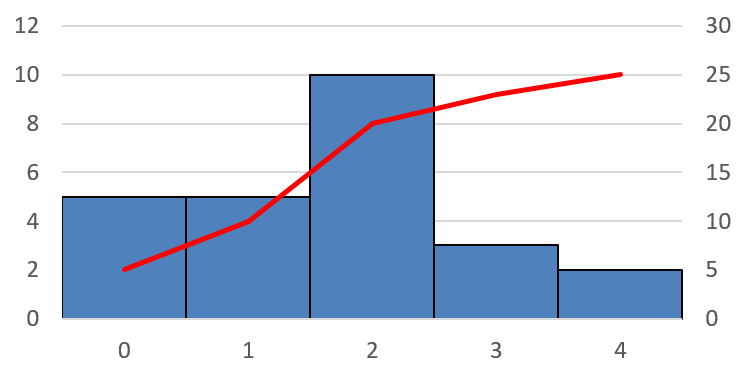
../_images/histoCumuleDemo.png

L’histogramme cumulé est une courbe croissante dont la valeur maximale est égale au nombre de pixel dans l’image.

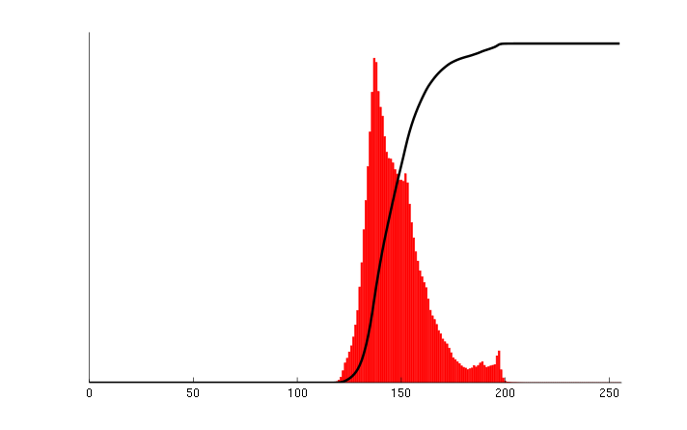
Dans l’exemple ci-dessous, l’histogramme cumulé comprend 2 phases presques plates (valeurs sombres et claires) et augmente brutalement dans les valeurs intermédaires : cette image est mal équilibrée.

badHisto badHistoCumul

On peut remarquer que, en notant \(N\) le nombre de pixel dans une image \(f\), pour une valeur de niveau de gris \(v\), \(C_f(v)/N\) est la proportion de pixels ayant une valeur inférieure ou égale à \(v\) dans l’image. Dans une image visuellement agréable, l’histogramme cumulé est proche de la diagonale, dans ce cas on devrait avoir \(v/n = C_f(v)/N\) : la proportion du niveau de gris \(v\) par rapport au niveau de gris maximal \(n\) est égale à la proportion de pixels ayant une valeur inférieure ou égale à \(v\) par rapport au nombre total de pixel.

En combinant cette observation avec le fait de vouloir obtenir une valeur minimale égale à \(V_{min}\) et une valeur maximale égale à \(V_{max}\), on obtient la formule d’égalisation d’histogramme:

\[\forall v\in[0..n], eg(v) = \frac{V_{max}-V_{min}}{N}C_f(v) + V_{min}\]

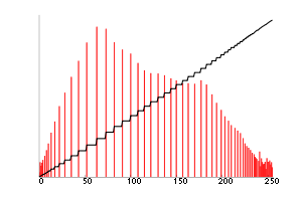
Appliquée à l’image précédente, on obtient le résultat suivant:

badHistoEg badHistoCumulEg

On peut observer que l’histogramme est bien étalé sur toute la plage de valeurs. L’histogramme cumulé est proche de la diagonale. Les niveaux de gris comprenant peu de valeurs sont tassés (visible sur les extrémités de l’histogramme), alors que les niveaux de gris comprenant beaucoup de pixels sont étalés (milieu de l’histogramme).

Implémentez cette transformation dans la fonction equalize du fichier tpHistogram.cpp. Pensez à valider votre implémentation avec la commande test.

Seuillage automatique

L’objectif de ce dernier exercice est de réutiliser les éléments acquis dans les exercices précédents pour comprendre et implémenter une transformation décrite dans un autre contexte.

La binarisation au moyen du seuillage combiné prend en paramètre un niveau de seuillage \(t\). Il existe différentes stratégie afin de déterminer un niveau de seuil automatiquement et ainsi avoir une fonction de seuillage sans paramètre.

La méthode d’Otsu fait partie des méthodes les plus connues pour cela. Elle est basée sur une approche classification : on considère que seuiller l’image à un niveau \(t\) revient à classifier les pixels de l’image en 2 classes blanc et noir. On peut alors mesurer la qualité d’un niveau de seuillage par la qualité de la classification qu’il génère. Seuiller l’image de manière automatique revient alors à trouver le niveau de seuil qui génère la meilleure classification des pixels.

Implémentez la méthode d’Otsu dans la fonction thresholdOtsu du fichier tpHistogram.cpp. Cette méthode est décrite sur de nombreux sites Web : documentation OpenCV, page Wikipedia…