Transformations géométriques
Les exercices à réaliser sont situés dans la base de code que vous récupérez en vous inscrivant sur le lien GitHub classroom reçu par mail [1]. Lisez bien le readme du dépôt pour comprendre comment l’utiliser. La majorité des fonctions demandées existent déjà dans OpenCV : le but n’est pas d’utiliser les fonctions d’OpenCV mais de les coder vous même ! Nous utiliserons donc uniquement les conteneurs de base d’OpenCV et les fontions d’entrée/sortie.
Important
Au cours de ce chapitre, vous compléterez le fichier ``tpGeometry.cpp`` que vous devrez pousser sur votre dépôt git avant la prochaine séance (cf. consignes détaillées envoyées par mail).
Transformations
Certaines transfromations géométriques sont triviales à réaliser car elles ne reposent que sur un jeu d’indices. Dans cette catégorie on retrouve notamment:
les translations par un vecteur de coordonnées entières,
les rotations d’angles multiples de \(90°\),
les symmétries verticales ou horizontales.
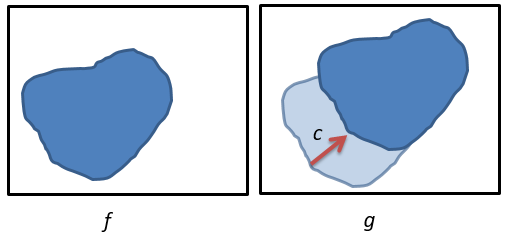
L’image g correspond à la translation de l’image f par le vecteur c. Formellement on a \(g(p)=f(p-c)\).

L’image g correspond à la transposée de l’image f. Formellement on a \(g((x,y))=f((y,x))\).
Implémentez la transposée d’image dans la fonction transpose du fichier tpGeometry.cpp. Pensez à valider votre implémentation avec la commande test.
Dans le cas général, une transformation géométrique est une fonction \(\phi:\mathbb{R}^2\rightarrow\mathbb{R}^2\) qui a chaque point du plan associe un autre point du plan. Toutes les transformations géométriques simples et leurs combinaisons entrent dans ce cadre : rotations, translations, homotéthies, symmétries…
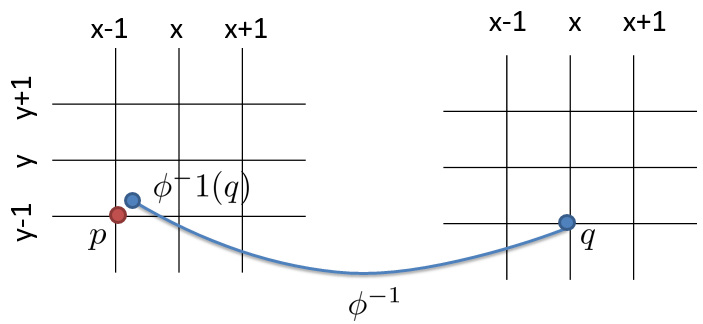
Néanmoins, l’application directe d’une transformation quelconque \(\phi\) pose problème car l’image d’un pixel \(p=(x,y)\in\mathbb{Z}^2\) de coordonnées entières par \(\phi\) ne donnera généralement pas un résultat en coordonnées entières : \(\phi(p)\notin\mathbb{Z}^2\) :
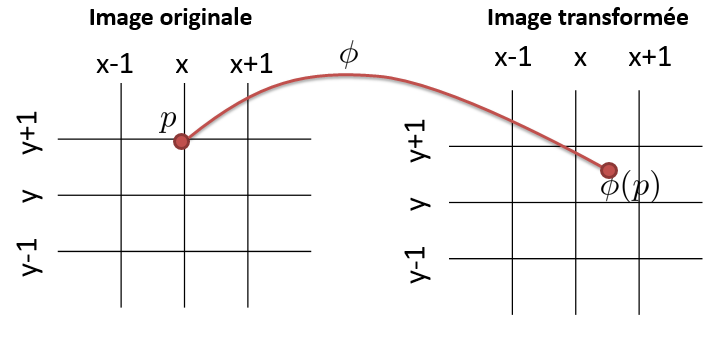
L’image du pixel \(p\) par la transformation \(\phi\) ne tombe pas exactement sur un pixel de l’image transformée : comment faire pour trouver les valeurs des pixels de l’image transformée ?
L’idée pour résoudre ce problème est d’inverser la question que l’on se pose : plutôt que de chercher la position d’un pixel de l’image d’origine après transformation, on va chercher quelle était la position d’un pixel de l’image résultat avant transformation. On va donc utiliser la transformation inverse \(\phi^{-1}\) :
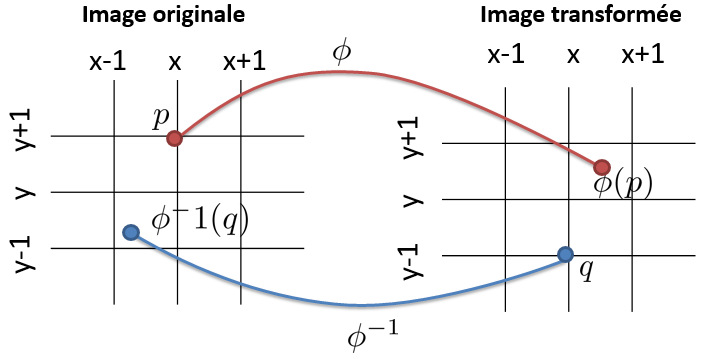
L’application inverse \(\phi^{-1}\) associe à chaque pixel de l’image transfomée un point dans l’image d’origine.
Mais l’image de \(\phi^{-1}(q)\) ne tombe pas non plus exactement sur un pixel de l’image d’origine ! Cette fois on peut néanmoins s’en sortir en interpolant la valeur de l’image d’origine au point \(\phi^{-1}(q)\) en utilisant les valeurs des pixels connues.
Interpolation 2D
Les 3 principales méthodes d’interpolation 2D sont :
plus proche voisin,
bilinéaire,
bicubique.
Schématiquement, on peut représenter ces 3 processus d’interpolation, en 1D et 2D de la manière suivante :
Dans ces illustrations, les valeurs des fonctions aux points rouges, jaunes, verts et bleus sont connues. Le but est de déterminer la valeur interpolée au niveau du point noir. Les courbes grises représentent les courbes interpolées. L’interpolation par plus proche voisin consiste à utiliser la valeur du point connu le plus proche. L’interpolation linéaire consiste à tracer des droites entre les points connus les plus proches : en 1D il faut 2 points, en 2D il en faut 4. L’interpolation cubique consiste à tracer des polynomes de degré 3 entre les points connus les plus proches : en 1D il faut 4 points, en 2D il en faut 16 (Source de l’image Wikipédia).
Sur une image ces 3 méthodes d’interpolation vont produire des images de plus en plus lisses :
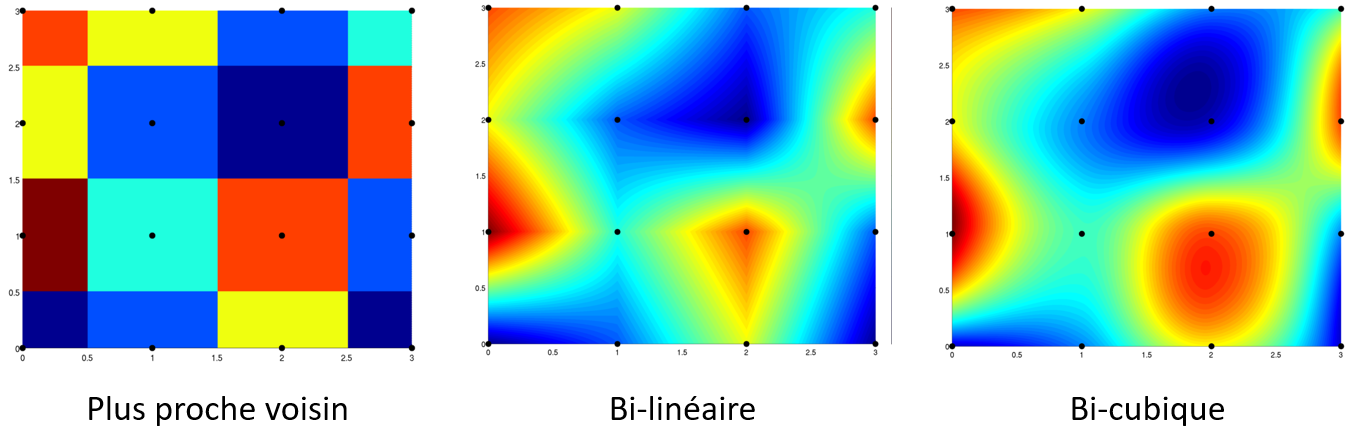
Effets des différentes interpolations sur une même image. Les points de l’image d’origine sont marqués en noir, tous les autres points sont interpolés à partir des valeurs des points noirs.
Nous allons voir le fonctionnement des 2 premières méthodes d’interpolation : par plus proche voisin et bilinéaire. L’interpolation bicubique n’est pas beaucoup plus compliquée en théorie mais sa mise en oeuvre est assez fastidieuse car il faut regarder la valeur de 16 points de l’images pour interpoler une valeur.
L’interpolation par plus proche voisin consiste simplement à attribuer à un point \(\phi^{-1}(q)\) de coordonnées réelles, la valeur du pixel \(p\) (de coordonnées entières) le plus proche de \(\phi^{-1}(q)\) :
Etant donnée une image \(f:\mathbb{Z}^2\rightarrow\mathbb{R}\), on peut définir l’image \(F:\mathbb{R}^2\rightarrow\mathbb{R}\) correspondant à l’interpolation par plus proche voisin de \(f\) de la manière suivante :
Notez que \(\lfloor x+0.5 \rfloor\) correspond à prendre l’arrondi de \(x\), c’est-à-dire l’entier le plus proche.
Implémentez l’interpolation par plus proche voisin dans la fonction interpolate_nearest du fichier tpGeometry.cpp. Implémentez la fonction expand du fichier tpGeometry.cpp qui agrandit une image en utilisant une fonction d’interpolation. Pensez à valider votre implémantion avec la commande test (l’exécutable généré s’appelle expand).
L’interpolation bilinéaire est construite à partir de l’interpolation linéaire 1D. En 1D, le principe est le suivant:
on connait la valeur de la fonction \(f\) aux points \(x_1\) et \(x_2\),
on souhaite interpoler \(f\) au point \(x_3\) tel que \(x_1 \leq x_3 \leq x_2\).
On fait l’hypothèse que \(f\) est affine (forme un segment de droite) sur l’intervalle \([x_1,x_2]\) :
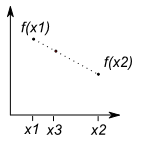
On déduit (c’est le même problème que la normalisation d’histogramme) :
Que l’on peut également écrire :
avec \(\alpha = \frac{x_3-x_1}{x_2-x1}\in[0,1]\) : \(\alpha\) représente la proportion de \(f(x_2)\) et \(1-\alpha\) la proportion \(f(x_1)\) dans \(f(x_3)\).
En 2D, on part du principe suivant :
on connait la valeur de la fonction \(f\) aux points \((x_1, y_1)\), \((x_1, y_2)\), \((x_2, y_1)\) et \((x_2, y_2)\),
on souhaite interpoler \(f\) au point \((x_3, y_3)\) tel que \(x_1 \leq x_3 \leq x_2\) et \(y_1 \leq y_3 \leq y_2\) :
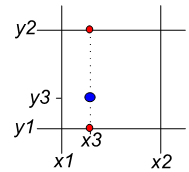
L’interpolation bilinéaire est réalisée en 3 étapes :
On réalise une interpolation 1D entre \((x_1, y_1)\), \((x_2, y_1)\) pour trouver la valeur de \(f\) au point \((x_3, y_1)\).
On réalise une interpolation 1D entre \((x_1, y_2)\), \((x_2, y_2)\) pour trouver la valeur de \(f\) au point \((x_3, y_2)\).
On réalise une interpolation 1D entre \((x_3, y_1)\), \((x_3, y_2)\), les 2 points interpolés précédemment, pour trouver la valeur de \(f\) au point \((x_3, y_3)\).
On peut montrer que ce processus revient à la formule suivante :
avec \(\alpha = \frac{x_3-x_1}{x_2-x1}\in[0,1]\) et \(\beta = \frac{y_3-y_1}{y_2-y1}\in[0,1]\).
Implémentez l’interpolation bilinéaire dans la fonction interpolate_bilinear du fichier tpGeometry.cpp. Pensez à valider votre implémantion avec la commande test (l’exécutable généré s’appelle expand).
Notez que pour appliquer la formule d’interpolation bilinéaire, on connait les coordonnées du point à interpoler \((x_3,y_3)\in\mathbb{R}^2\) mais il faut déterminer les coordonnées des points \((x_1,y_1)\in\mathbb{Z}^2\) et \((x_2,y_2)\in\mathbb{Z}^2\). Remarquez qu’on peut fixer \(x_1=\lfloor x_3 \rfloor\) et \(y_1=\lfloor y_3 \rfloor\).
Implémentez la transformation de rotation d’image dans la fonction rotate du fichier tpGeometry.cpp. Pensez à valider votre implémantion avec la commande test (l’exécutable généré s’appelle rotate).
Le choix de la fonction d’interpolation est particulièrement important dans le cas de la rotation. En prenant l’image ci-dessous :
une rotation avec les différentes méthodes d’interpolations donnent les résultats suivants :

On voit clairement des effets d’aliasing (des lignes continues deviennent discontinues) apparaitrent avec l’interpolation par plus proche voisin. L’interpolation bilinéaire améliore la situation, mais le contraste est diminué. L’interpolation bicubique donne le meilleur résultat.
Notez que la rotation change en générale la taille de l’image. Ici, on choisit de laisser les parties de l’image transformée qui ne tombent pas dans l’image d’origine en noir.