Convolution
Les exercices à réaliser sont situés dans la base de code que vous récupérez en vous inscrivant sur le lien GitHub classroom reçu par mail [1]. Lisez bien le readme du dépôt pour comprendre comment l’utiliser. La majorité des fonctions demandées existent déjà dans OpenCV : le but n’est pas d’utiliser les fonctions d’OpenCV mais de les coder vous même ! Nous utiliserons donc uniquement les conteneurs de base d’OpenCV et les fontions d’entrée/sortie.
Important
Au cours de ce chapitre, vous compléterez le fichier ``tpConvolution.cpp`` que vous devrez pousser sur votre dépôt git avant la prochaine séance (cf. consignes détaillées envoyées par mail).
Filtre moyenneur
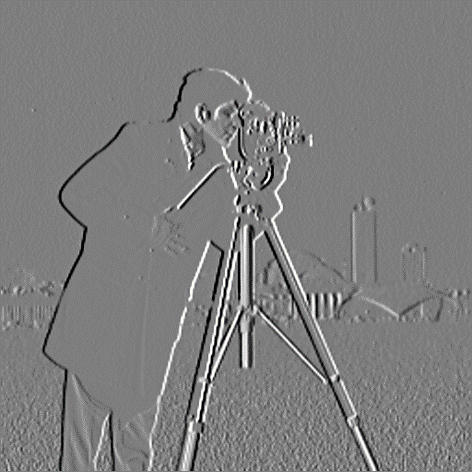
Le filtre moyenneur est une opération de traitement d’images utilisée pour réduire le bruit dans une image et/ou flouter une image. Par exemple, l’application d’un filtre moyenneur sur l’image de gauche donne l’image de droite :
En zoomant, on peut voir en détail les effets du filtre; le bruit clairement visible dans le ciel a bien été réduit mais les détails du visage et de la caméra sont floutés :
Le filtre moyenneur fait parti de la catégorie des filtres d’images locaux car pour calculer la nouvelle valeur d’un pixel, il regarde la valeur des pixels proches. Concrètement, la valeur filtrée d’un pixel \(p\) est égale à la moyenne des valeurs des pixels proches de \(p\). En général, on définit les « pixels proches de \(p\) » comme l’ensemble de pixels contenus dans un carré de largeur \(k\) centré sur \(p\) :
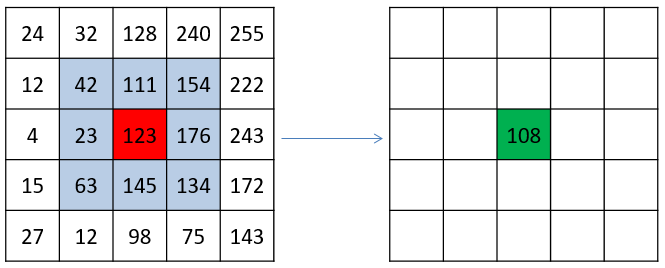
Avec un filtre moyenneur de largeur \(3\), pour calculer la nouvelle valeur du pixel rouge de l’image originale de gauche, on calcule la valeure moyenne des pixels situés dans un carré de dimension \(3\times 3\) centré sur ce pixel. Cela donne la nouvelle valeur du pixel sur l’image transformée (pixel vert sur l’image de droite) : \(\frac{42+111+154+23+123+176+63+145+134}{9}=108\)
Cette opération est répétée pour tous les pixels de l’image. On parle de fenêtre glissante pour caractériser le carré sur lequel est calculé la moyenne des pixels et qui se déplace sur l’image :
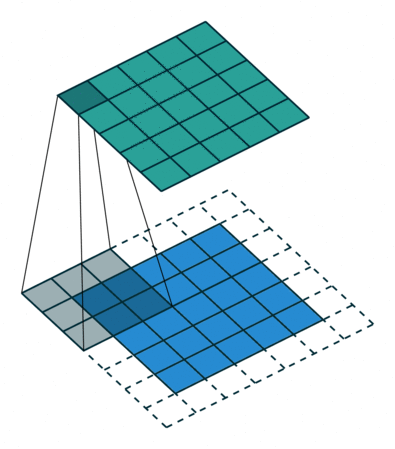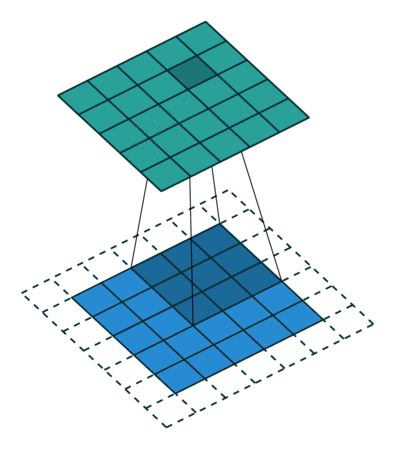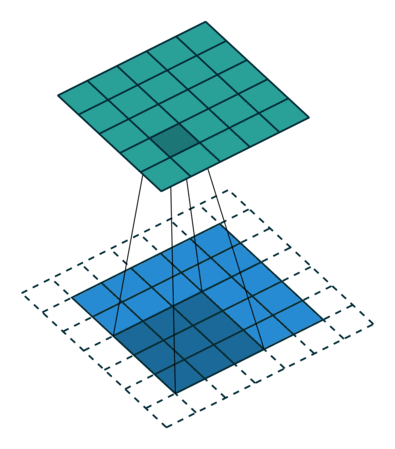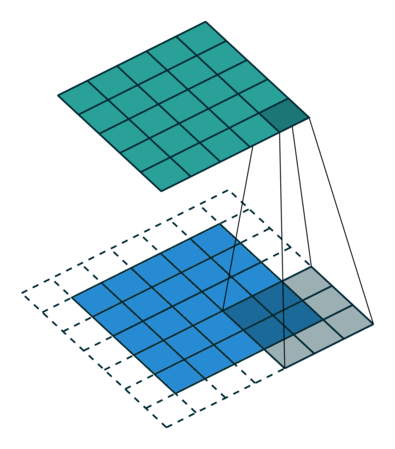
Illustration du principe de la fenêtre glissante. La fenêtre se déplace sur l’image du bas (en bleu) pour calculer les valeurs de la nouvelle image en haut (en vert). Source https://github.com/vdumoulin/conv_arithmetic.
Implémentez le filtre moyenneur dans la fonction meanFilter du fichier tpConvolution.cpp. Pensez à valider votre implémantion avec la commande test.
Notez que pour une valeur de paramètre \(k\), la fenêtre de calcul à utiliser est de taille \(2k+1\) : cette pratique commune permet de garantir que la fenêtre considérée est de dimension impaire et donc que son centre tombe précisément sur un pixel de coordonnées entières.
Convolution
La convolution, ou produit de convolution, est une généralisation du filtre moyenneur où l’on considère cette fois une moyenne pondérée. La fenêtre glissante est alors elle même une image qui contient les coefficients de pondération. On l’appelle généralement noyau de convolution ou masque de convolution (kernel ou mask en anglais) :
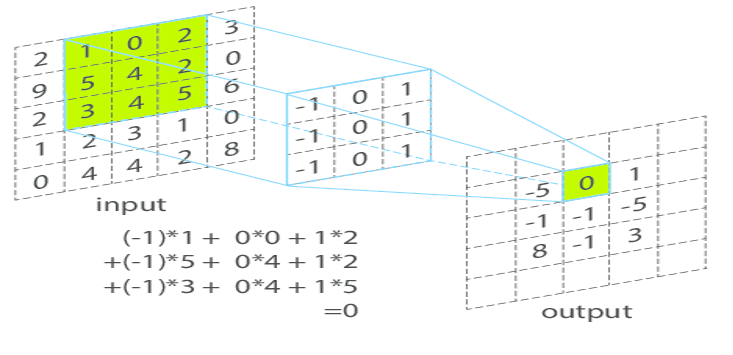
Le noyau de convolution (au centre) contient les coefficients de pondération. Le principe est alors similaire au filtre moyenneur : pour calculer la nouvelle valeur d’un pixel à droite, on calcule la moyenne des pixels de l’image originale (à gauche) se trouvant sous le masque de convolution pondérée par les valeurs du masque.
Formellement, le produit de convolution est une opération entre deux images en niveau de gris \(f\) et \(g\), notée \(f*g\) défini par:
Dans cette expression on peut reconnaitre:
\(g(x-i,y-j)\) : qui comporte une opération de translation par le vecteur \((x,y)\) et une symétrie centrale (inversion des coordonnées \(i\) et \(j\)) : il s’agit du déplacement de l’image \(g\) à la position \((x,y)\) (\(g\) joue donc le rôle de fenêtre glissante). La symétrie centrale est présente pour une raison technique et n’a pas vraiment d’importance en pratique,
la multiplication point à point de \(f\) par la translatée de \(g\) : c’est l’opération de pondération,
la sommation du tout : c’est l’opération de moyennage.
Le produit de convolution est une application bilinéaire, associative et commutative. C’est-à-dire que pour toutes images \(f\), \(g\), \(h\) et pour tout scalaire \(\lambda\), on a :
\(f\ast (g+\lambda h)=(f\ast g)+\lambda (f\ast h)\);
\((f\ast g)\ast h=f\ast (g\ast h)\);
\(f\ast g=g\ast f\).
Le choix du noyau de convolution va permettre d’obtenir différents effets :
Effet |
Noyau |
Résultat |
|---|---|---|
Identité (ne fait rien…) |
\(\begin{bmatrix} 1\end{bmatrix}\) |
|
Filtre moyenneur (lissage) |
\(\frac{1}{9}\begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1\end{bmatrix}\) |
|
Filtre gaussien \(3 \times 3\) (lissage) |
\(\frac{1}{16}\begin{bmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1\end{bmatrix}\) |
|
Filtre gaussien \(5 \times 5\) (lissage) |
\(\frac{1}{256}\begin{bmatrix} 1 & 4 & 6 & 4 & 1 \\ 4 & 16 & 24 & 16 & 4 \\ 6 & 24 & 36 & 24 & 6 \\ 4 & 16 & 24 & 16 & 4 \\ 1 & 4 & 6 & 4 & 1 \end{bmatrix}\) |
|
Filtre réhausseur (renforce les contours) |
\(\begin{bmatrix} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0\end{bmatrix}\) |
|
Filtre Laplacien (détecteur de contours) |
\(\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0\end{bmatrix}\) |
|
Implémentez le produit de convolution dans la fonction convolution du fichier tpConvolution.cpp. Pensez à valider votre implémantion avec la commande test.
Note
Le produit de convolution est intimement lié à la transformée de Fourier par le théorème de la convolution. En effet si on note par \(F\) et \(F^{-1}\) la tranformée de Fourier et la transformée de Fourier inverse, on a l’égalité suivante :
ou \(\circ{}\) représente la multiplication point à point, aussi appelé produit d’Hadamard (on multiplie les 2 valeurs d’un même pixel dans les 2 images).
Autrement dit, pour calculer \(f * g\), on peut procéder ainsi :
on calcule les transformées de Fourier des images \(f\) et \(g\),
on multiple les 2 résultats des transformées de Fourier entre eux,
on prend la transformée de Fourier inverse du résultat de la multiplication.
Cette approche présente une complexité algorithmique inférieure au calcul naïf grâce à l’algorithme de transformée de Fourier rapide (Fast Fourier Transform (FFT)). Néanmoins, la constante multiplicative est plus élevée qu’avec l’approche naïve et la convolution de Fourier n’est intéressante que lorsque le noyau de convolution est relativement grand (plusieurs dizaines de pixels de côté).
Détection de contours
La détection de contours consiste à chercher les courbes continues le long des zones de fortes variations dans l’image. Les expériences en neurosciences ont en effet montrés que la détection de contours est une des premières étapes réalisées par le cortex visuel, suggérant leur importance pour les processus d’analyse d’images.
Note
L’étude du cortex visuel à notamment progressé grâce à une série d’expériences menées sur des chats dans les années 60. Une des expériences constistait par exemple à élever un chaton dans un environnement où seules des lignes verticales sont visibles; après quelques semaines, on constatait alors l’absence de réponse du cortex visuel en présence de lignes horizontales, montrant ainsi que le cerveau du chat, en l’absence de stimulation appropriée, n’a pas pû « entrainer son détecteur de contours » sur l’axe horizontal. Plus d’information sur ce site

La détection de zones de variation des niveaux de gris de l’image correspond à l’opération de dérivation. Comme une image numérique n’est pas une fonction continue, la notion de dérivée n’est pas formellement définie et on utilisera un analogue appelé gradient. Comme une image a 2 dimensions, le gradient de l’image \(f\), notée \(\nabla f\), est une image vectorielle, donnée par les deux dérivées partielles :
Sur l’exemple ci-dessous, on peut observer une image et ses 2 dérivées partielles. On constate que les variations horizontales (respectivement verticales) apparaissent dans la dérivée partielle \(\frac{\partial f}{\partial x}\) (respectivement \(\frac{\partial f}{\partial y}\)).
\(f\) |
\(\frac{\partial f}{\partial x}\) |
\(\frac{\partial f}{\partial y}\) |
On peut également regarder le vecteur du gradient sous sa forme polaire \((||\nabla f||, dir(\nabla f))\), avec :
\(||\nabla f||\) la norme du gradient : \(||\nabla f|| = \sqrt{\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2}\) ou, pour simplifier les calculs \(||\nabla f|| = \left|\frac{\partial f}{\partial x}\right|+\left|\frac{\partial f}{\partial y}\right|\)
et \(dir(\nabla f)\) la direction du gradient : \(dir(\nabla f)=\textrm{atan2}\left(\frac{\partial f}{\partial y},\frac{\partial f}{\partial x}\right)\)
Cela donne les images suivantes (notez que les niveaux de gris de \(dir(\nabla f)\) représente des angles et son interprétation visuelle n’est donc pas évidente) :
\(f\) |
\(||\nabla f||\) |
\(dir(\nabla f)\) |
En pratique, il n’existe pas de définition unique pour le calcul des dérivées partielles \(\frac{\partial f}{\partial x}\) et \(\frac{\partial f}{\partial y}\). Plusieurs solutions exprimables sous forme de produit de convolution ont été proposées, celle que nous allons voir est appellée gradient de Sobel.
La méthode de Sobel définit les dérivées partielles de la manière suivante :
et
Le choix de ces noyaux peut s’expliquer en décomposant les noyaux de convolution selon leur contribution dans chacune des dimensions. Par exemple, pour la dérivée partielle selon \(x\), on a :
Dit autrement, le produit de convolution étant un application linéaire, on peut réécrire la définition de \(\frac{\partial f}{\partial x}\) sous la forme :
C’est à dire qu’on commence par convoluer \(f\) avec le noyau vertical, puis on convolue avec le noyau horizontal :
la première convolution réalise un lissage de l’image sur l’axe vertical (le noyau utilisé est la colonne centrale du noyau gaussien \(3 \times 3\)),
la deuxième convolution calcule, pour chaque pixel \(p\), la différence entre le pixel à droite de \(p\) et le pixel à gauche de \(p\) (c’est donc une mesure de variation).
Implémentez la fonction edgeSobel du fichier tpConvolution.cpp qui calcule la norme du gradient selon la méthode de Sobel. Pensez à valider votre implémantion avec la commande test.
Filtre bilatéral
L’objectif de ce dernier exercice est de réutiliser les éléments acquis dans les exercices précédents pour comprendre et implémenter une transformation décrite dans un autre contexte.
L’opération de convolution est efficace pour débruiter une image et lisser les zones texturées. Malheureusement, elle a également une forte tendance à flouter les contours. Il existe une variation de l’opération de convolution appelée filtre bilatéral qui résoud ce problème en introduisant une seconde pondération afin de ne pas donner trop de poids à un pixel dont la valeur est éloignée de la valeur du pixel courant.
Implémentez le filtre bilatéral dans la fonction bilateralFilter du fichier tpConvolution.cpp. Pensez à valider votre implémantion avec la commande test.
Cette méthode est décrite sur de nombreux sites Web, par exemple https://people.csail.mit.edu/sparis/bf_course/slides/03_definition_bf.pdf