Morphologie Mathématique

Les exercices à réaliser sont situés dans la base de code que vous récupérez en vous inscrivant sur le lien GitHub classroom reçu par mail [1]. Lisez bien le readme du dépôt pour comprendre comment l’utiliser. La majorité des fonctions demandées existent déjà dans OpenCV : le but n’est pas d’utiliser les fonctions d’OpenCV mais de les coder vous même ! Nous utiliserons donc uniquement les conteneurs de base d’OpenCV et les fontions d’entrée/sortie.

Important

Au cours de ce chapitre, vous compléterez le fichier ``tpMorphology.cpp`` que vous devrez pousser sur votre dépôt git avant la prochaine séance (cf. consignes détaillées envoyées par mail).

Filtre médian

L’idée du filtre médian reprend le principe de la fenêtre glissante mais ne s’intéresse pas à une combinaison linéaire des valeurs des pixels dans la fenêtre (contrairement au produit de convolution). Au lieu de cela, on va trier les pixels situés sous la fenêtre par ordre de niveau de gris croissant et prendre le pixel se trouvant au milieu : on parle d’élément médian.

Par exemple, si l’on considère la liste de valeur \((1, 3, 6, 9, 223)\) : cette liste est triée et comporte 5 éléments; le médian de cette liste est le 3ème élément, c’est-à-dire le 6. Par rapport à la moyenne, le médian à l’avantage d’être robuste aux valeurs extrêmes qui ne sont pas forcément représentatives de la distribution des valeurs dans la liste. Dans le cas précédent, la moyenne vaut \(48.4\), elle est fortement influencée par la valeur \(223\) qui n’est pas vraiment représentative du reste des éléments de la liste. Alors que le médian à \(6\) semble effectivement mieux représenter les valeurs de la liste.

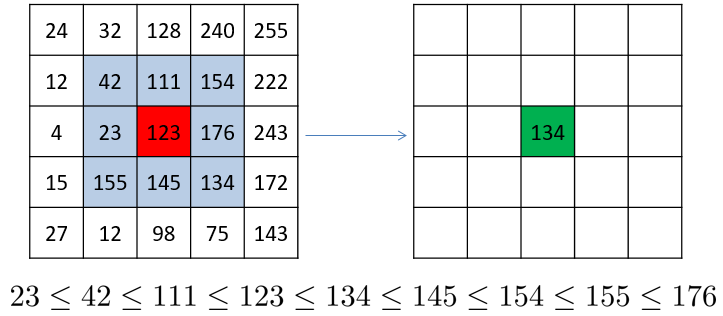
../_images/median.png — Calcule du filtre médian sur une image. La fenêtre est représentée en bleue sur l’image d’origine (à gauche). Les valeurs dans la fenêtre sont triées (ligne du bas) et l’élément médian (134) est utilisé comme nouvelle valeur sur le résultat (à droite).

Note

Les statistiques de l’INSEE sur les salaires en France présentent toujours des valeurs médianes et non des moyennes, sinon les très hauts revennus influenceraient fortement le résultat sans pour autant être représentatifs de la population.

Le filtre médian est particulièrement efficace pour réduire le bruit poivre et sel où les pixels sont aléatoirement transformés en pixels blancs ou noirs :

../_images/exMedian.png — Exemple d’application du filtre médian pour réduire le bruit poivre et sel d’une image. A gauche : image originale. Au centre : image artificiellement bruitée par du bruit poivre et sel, 1/10ème des pixels ont été aléatoirement transformés en pixels noirs ou blancs. A droite : résultat d’application d’un filtre médian \(3 \times 3\) sur l’image bruitée. On constate que l’image est bien débruitée. Le filtre médian introduit moins de flou que le filtre moyenneur.

Implémentez le filtre médian dans la fonction median du fichier tpMorphology.cpp. Pensez à valider votre implémantion avec la commande test.

Erosion et dilatation

L’érosion et la dilatation sont deux opérations opposées de la morphologie mathématique. Alors que les filtres vus jusqu’à présent se concentrent sur la modification de niveaux de gris des pixels, la morphologie mathématique cherche à modifier la forme des objets. Ainsi, le rôle d’une érosion est de réduire la taille des objets dans une image alors que la dilatation va chercher à les agrandir.

Dilatation

L’opération de dilatation utilise la notion d’élément structurant qui généralise le concept de fenêtre glissante. L’idée est que, pour pouvoir étudier la forme des objets, il faut pouvoir considérer des fenêtres glissantes avec des formes plus complexe qu’un carré : par exemple des segments, des cercles, des triangles. Dans la pratique, un élément structurant sera simplement une image binaire qui contient la forme d’intérêt.

La dilatation d’une image à niveaux de gris \(f:\mathbb{Z}^2\rightarrow\mathbb{R}\) par une image binaire \(SE\subseteq\mathbb{Z}^2\) (l’élément structurant) est notée \(f \oplus SE\) ou \(\delta_{SE}(f)\). Après dilatation, la nouvelle valeur d’un pixel est donnée par la valeur maximale des pixels sous l’élément structurant :

\[\forall x, (f\oplus SE)(x) = \delta_{SE}(f)(x) = \max_{p \in SE}f(x+p)\]

Comparé au filtre médian : la fenêtre n’est plus carré et on prend l’élément \(\max\) au lieu du médian. Afin de bien visualiser le résultat de cette opération, il est plus simple de se limiter aux images binaires dans un premier temps :

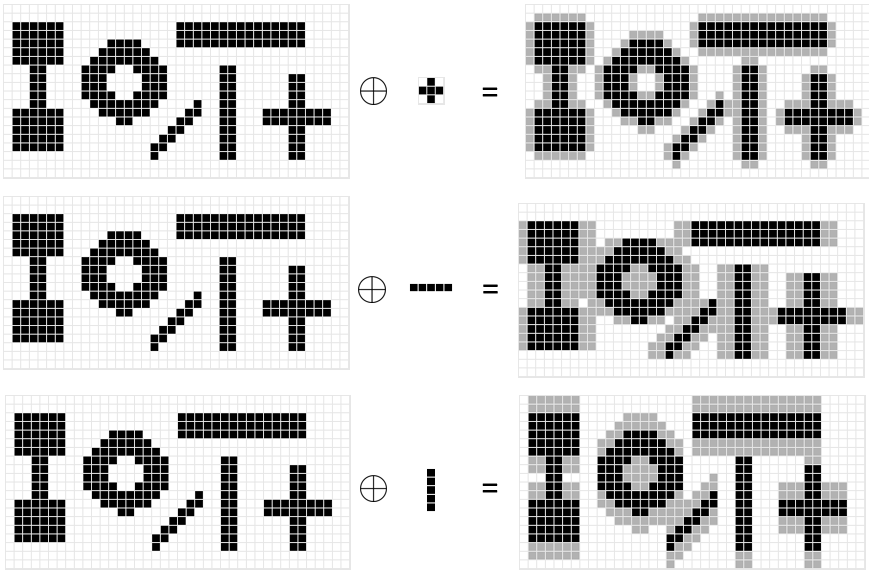
../_images/dilationBin.png — Exemple de dilatations sur des images binaires. Sur la colonne de gauche, on voit l’image originale binaire : les pixels noirs sont considérés comme faisant partis de l’image. Sur la colonne du milieu, on voit les 3 éléments structurants : 1 croix, 1 segment horizontal et 1 segment vertical. La colonne de droite montre le résultat de la dilatation de l’image par l’élément structurant : le résultat est une image binaire où les pixels noirs et gris font partis de l’image (les pixels gris ont étés ajoutés à l’image de gauche par la dilatation). On voit que la dilatation agrandit les objets présents dans l’image et que la direction et la taille de cet agrandissement dépendent de la forme de l’élément structurant.

Dans le cas des images à niveau de gris, on voit que la dilatation tend à agradandir les zones claires selon la forme de l’élément structurant :

Dilatation de l’image camera par un élément structurant circulaire, horizontal et vertical (de gauche à droite).

Implémentez la dilatation dans la fonction dilation du fichier tpMorphology.cpp. Pensez à valider votre implémantion avec la commande test.

Erosion

L’érosion est obtenue de manière similaire à la dilatation en remplaçant \(\max\) par \(\min\). Soient une image à niveau de gris \(f:\mathbb{Z}^2\rightarrow\mathbb{R}\) et une image binaire \(SE\subseteq\mathbb{Z}^2\) (l’élément structurant), l’érosion de \(f\) par \(SE\) est notée \(f \ominus SE\) ou \(\epsilon_{SE}(f)\) et est définie par :

\[\forall x, (f\oplus SE)(x) = \epsilon_{SE}(f)(x) = \min_{p \in SE}f(x+p)\]

Comme pour la dilatation, afin de bien visualiser le résultat de cette opération, il est plus simple de se limiter aux images binaires dans un premier temps :

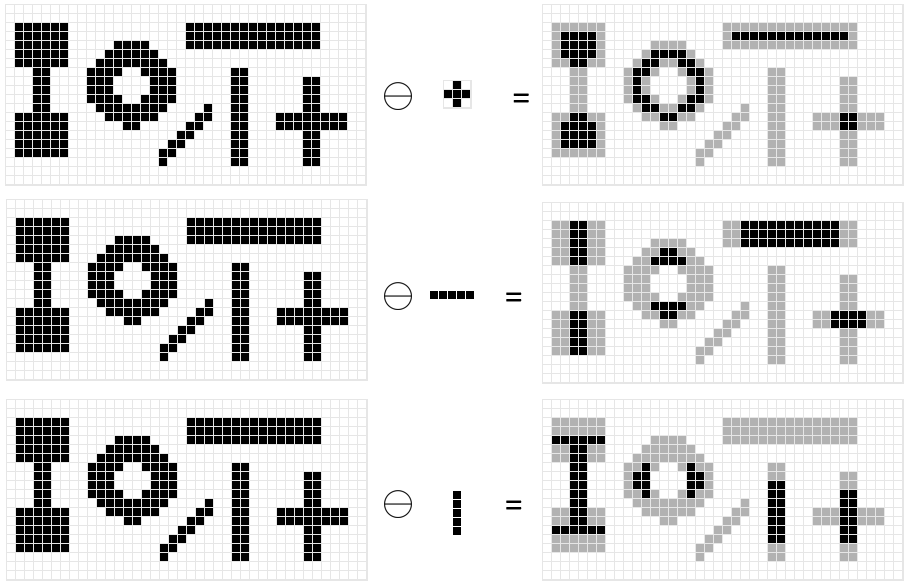
../_images/erosionBin.png — Exemple d’érosions sur des images binaires. Sur la colonne de gauche, on voit l’image originale binaire : les pixels noirs sont considérés comme faisant partis de l’image. Sur la colonne du milieu, on voit les 3 éléments structurants : 1 croix, 1 segment horizontal et 1 segment vertical. La colonne de droite montre le résultat de la dilatation de l’image par l’élément structurant : le résultat est une image binaire où les pixels noirs font partis de l’image (les pixels gris ont étés retirés à l’image de gauche par l’érosion). On voit que l’érosion réduit la taille les objets présents dans l’image et que la direction et la taille de ce rétrécissement dépendent de la forme de l’élément structurant.

Dans le cas des images à niveau de gris, on voit que l’érosion tend à agradandir les zones sombres selon la forme de l’élément structurant :

Erosion de l’image camera par un élément structurant circulaire, horizontal et vertical (de gauche à droite).

Important

Erosion et dilatation sont des opérations duales, cela veut dire que, étant donnée une image \(f\) et un élément structurant \(SE\) :

dilater l’inverse d’une image est la même chose que prendre l’inverse de l’érosion de cette image : \(\delta_{SE}(f) = -\epsilon_{SE}(-f,)\)
eroder l’inverse d’une image est la même chose que prendre l’inverse de la dilation de cette image : \(\epsilon_{SE}(f) = -\delta_{SE}(-f)\)

Cette situation est illustrée dans l’exemple ci-dessous :

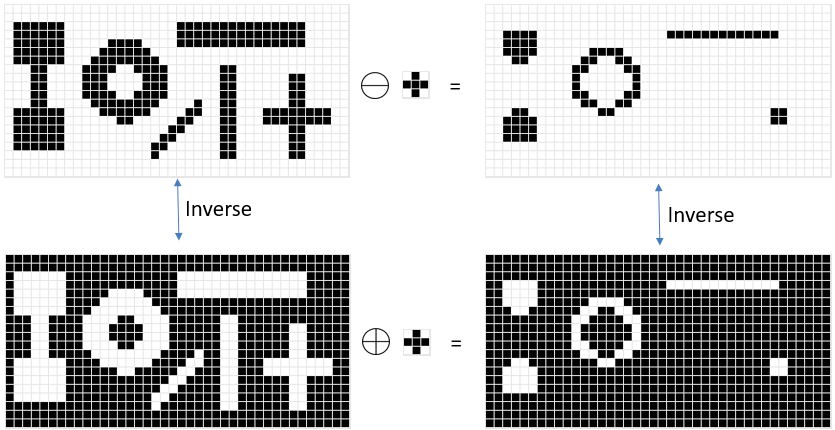
Implémentez l’érosion dans la fonction erode du fichier tpMorphology.cpp. Pensez à valider votre implémantion avec la commande test.

Vous pouvez réutiliser la fonction dilate grâce à la dualité entre érosion et dilatation.

Ouverture et fermeture

La composition des opérations de dilatation et d’érosion permet de produire de nouveaux opérateurs. Les deux plus simples sont la fermeture et l’ouverture.

Pour un élément structurant \(SE\), la fermeture \(\gamma_{SE}\) est définie comme une dilatation suivie d’une érosion : \(\phi_{SE}=\epsilon_{SE} \circ \delta_{SE}\). Cette opération bouche les trous plus petits que l’élément structurant et laisse le reste presque inchangé :

../_images/fermetureBin.png — Example de fermetures avec un élément structurant horizontal (colonne de gauche) et vertical (colonne de droite). La première ligne montre l’image de départ. La deuxième ligne montre le résultat de la dilatation. La dernière ligne montre le résultat final de la fermeture (érosion des images de la ligne précédente). L’opération de fermeture a *rempli* les espaces vides dans lequel il ne pouvait pas tenir entièrement.

Sur une image en niveau de gris, la fermeture va éclaircir les petites zones sombres :

../_images/cameraClose.png — Fermeture sur l’image camera

Pour un élément structurant \(SE\), l’ouverture \(\phi_{SE}\) est définie comme une érosion suivie d’une dilatation : \(\phi_{SE}=\delta_{SE} \circ \epsilon_{SE}\). Cette opération supprime les éléments plus petits que l’élément structurant et laisse les autres presque inchangés.

../_images/ouvertureBin.png — Example d’ouvertures avec un élément structurant en croix (colonne de gauche) et horizontal (colonne de droite). La première ligne montre l’image de départ. La deuxième ligne montre le résultat de l’érosion. La dernière ligne montre le résultat final de l’ouverture (dilatation des images de la ligne précédente). L’opération d’ouverture a *supprimé* les éléments dans lequel il ne pouvait pas tenir entièrement.

Sur une image en niveau de gris, l’ouverture va supprimer les petits éléments clairs:

../_images/cameraOpen.png — Ouverture sur l’image camera

Note

Tout comme l’érosion et la dilatation, ouveture et fermeture sont des opérations duales.

L’ouverture et la fermeture sont des opérations idempotentes : cela veut dire que l’application répétée d’un de ces opérateurs ne sert à rien : pour tout image \(f\) et tout élément structurant \(SE\), on a :

\(\phi_{SE}(\phi_{SE}(f)) = \phi_{SE}(f)\) et
\(\gamma_{SE}(\gamma_{SE}(f)) = \phi_{SE}(f)\).

Implémentez la fermeture dans la fonction close du fichier tpMorphology.cpp. Pensez à valider votre implémantion avec la commande test.

Implémentez l’ouverture dans la fonction open du fichier tpMorphology.cpp. Pensez à valider votre implémantion avec la commande test.

Gradient morphologique

Les opérateurs morphologiques permettent également de construire un gradient morphologique, contrepartie morphologique de la notion de gradient linéiare vue dans le chapitre sur le convolution. Pour une image \(f\) et un élément structurant \(SE\), on va définir un gradient interne, un gradient externe et un gradient morphologique. Les exemples présentés sont basés sur un élément structurant en forme de croix et sur l’image binaire habituelle :

Le gradient interne est défini par \(f-(f\ominus SE)\) la différence entre l’image et son érodé, c’est-à-dire l’ensemble des pixels retirés par l’érosion. On obtient le résultat suivant :
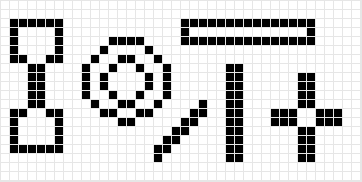
Le gradient externe est défini par \((f\oplus SE)-f\) la différence entre le dilaté et l’image, c’est-à-dire l’ensemble des pixels ajoutés par la dilatation. On obtient le résultat suivant :
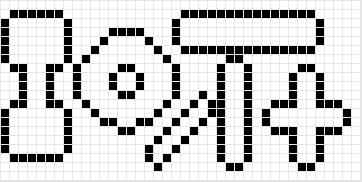
Le gradient morphologique est défini par \((f\oplus SE)-(f\ominus SE)\) combinaison des deux approches précédentes.On obtient le résultat suivant :

L’application sur des images à niveaux de gris se fait sans problème :

A gauche : image originale. A droite : gradient morphologique de l’image.

Implémentez le gradient morphologique dans la fonction morphologicalGradient du fichier tpMorphology.cpp. Pensez à valider votre implémantion avec la commande test.