Modélisation

Comment l’intelligence artificielle peut-elle traiter des problèmes très variés et reposant sur des données de nature très différente : images, sons ou textes ? Dans ce chapitre, nous répondons à cette question en montrant que toute problématique, indépendamment de sa forme initiale, peut être formulée comme un problème purement numérique.

Les données en entrée

Différents univers

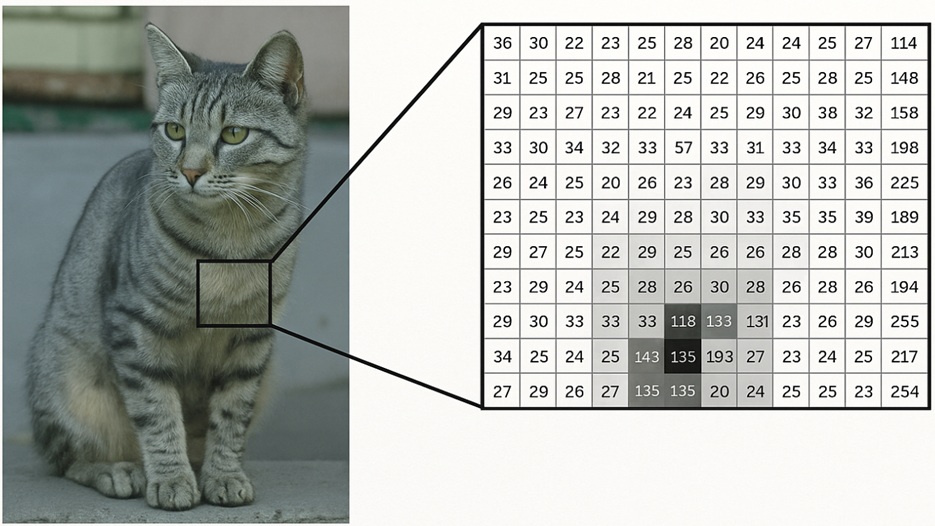
• Image : En premier lieu, on peut citer les images : par nature, elles sont déjà représentées sous la forme d’une grille bidimensionnelle de pixels, chacun décrit par trois valeurs (RGB). Cette structure correspond directement à un tenseur de données, aisément exploitable comme entrée d’un réseau de neurones. On pourra ainsi utiliser un tenseur 3D : 3 x L x H

  

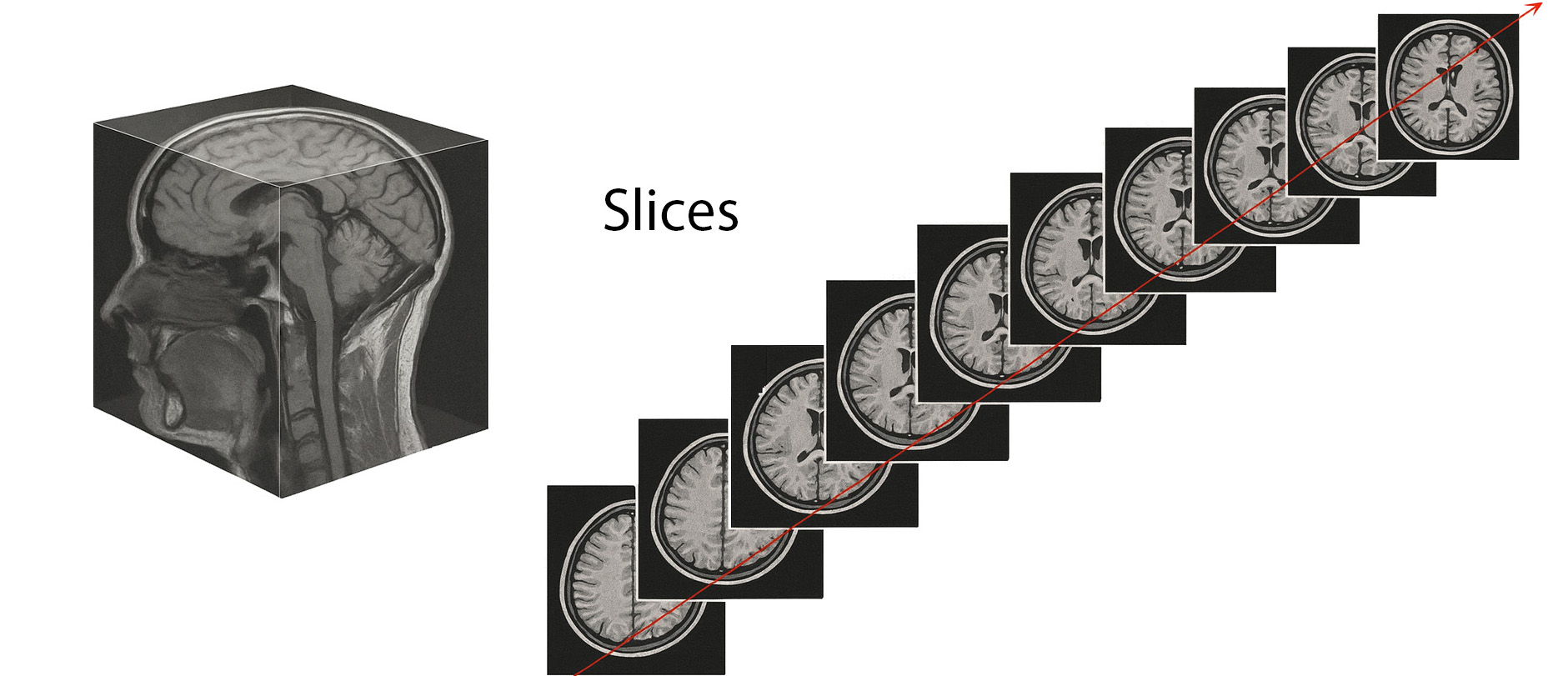
• IRM/SCAN : Chaque acquisition (~2 secondes) récupère une tranche appelée slice, composée de voxels 3D. L’empilement de ces tranches permet de reconstruire une représentation 3D du corps humain. Comme pour les images, ce type de données se traduit immédiatement en tenseur 3D : nb slices x L x H

  

• Vidéo : Une vidéo peut être vue comme une suite d’images (frames). Ainsi, comme pour le scanner 3D, la vidéo est stockée sous la forme d’un tenseur 4D : nb frames x 3 x L x H

  

• Parole : Grâce à un enregistreur audio, nous récupérons un signal échantillonné à 44 kHz, qui se traduit par un vecteur 1D de données :

  

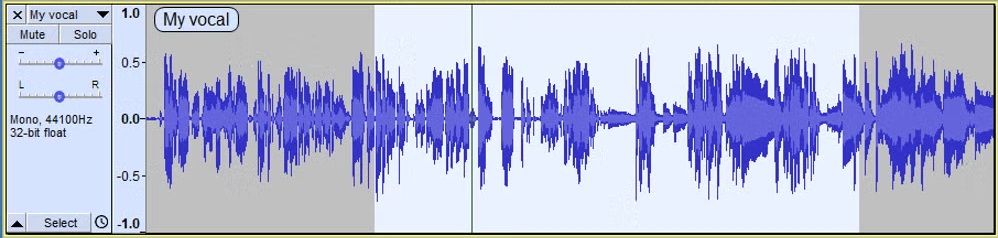
• Météo : Plusieurs données météorologiques, regroupant température, pression et hygrométrie, peuvent être regroupées dans un vecteur. Échantillonnées à intervalles réguliers, on peut ainsi les stocker dans un tenseur 2D : nb mesures x nb échantillons

  

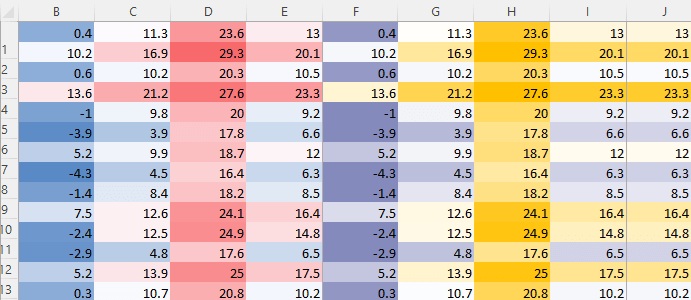
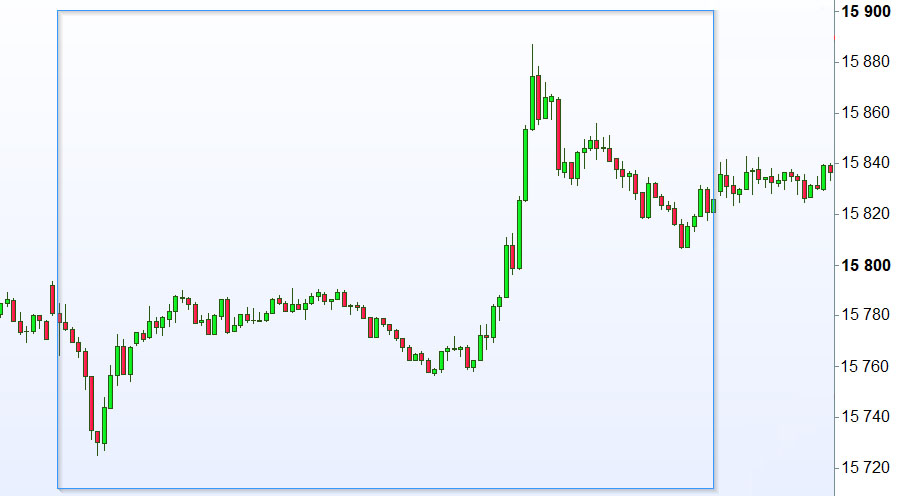
• Finance : Dans le cadre de l’analyse des signaux boursiers, nous récupérons des données très proches de celles de la météo. Ainsi, pour un intervalle de temps choisi (1 s, 1 min, 1 heure, 1 jour…), nous avons une bougie sur le graphique représentant 4 valeurs OHLC : Opening, Highest, Lowest, Closing. Nous pouvons donc stocker ce signal boursier dans un tenseur 2D : nb échantillons x 4

  

• IA et jeux : Prenons l’exemple du jeu d’échecs. Sa structure se prête naturellement à une représentation matricielle, mais il est nécessaire de choisir un codage compatible avec le deep learning. Une représentation naïve consisterait à attribuer un identifiant numérique à chaque type de pièce (1=pion noir, 2=fou noir…) et à coder l’échiquier sous la forme d’une matrice 8×8. Cependant, ce codage introduit une relation artificielle entre les pièces : un simple décalage de valeur pourrait, par exemple, transformer un pion en fou. Il est donc préférable d’utiliser un encodage différent, avec une matrice par type de pièce. Pour la matrice associée aux pions noirs, la valeur 1 indique la présence d’un pion à la position indiquée. Le plateau de jeu est ainsi représenté par un tenseur de dimension 12×8×8 car il y a en tout 12 types de pièces.

Normalisation

Même si chaque échantillon est stocké dans un tenseur 1D / 2D / 3D / 4D, il est fort probable que les différents échantillons soient de dimensions différentes :

• Image : résolutions différentes, format paysage ou portrait

• Scan 3D : appareils différents, avec des voxels plus ou moins fins (0.3 mm ou 0.1 mm)

• Vidéo / parole : durées différentes

Ainsi, on utilise des stratégies de normalisation de taille :

• Troncature : on coupe à une longueur maximale

• Padding : on complète les zones vides avec des zéros ou en utilisant des symétries

• Fenêtrage : on découpe le signal en segments de taille fixe

• Représentation intermédiaire :

  • Analyse par spectrogramme pour le son

  • Transformation du texte en vecteurs de tokens

On peut remarquer que la normalisation s’effectue également au niveau des plages de valeurs :

• Par exemple, entre une image correctement exposée et une image plus sombre, les intensités de pixels peuvent varier d’un facteur deux ou trois. Sans normalisation, ces écarts introduisent un biais lié à l’illumination. Il est donc d’usage de recentrer et de mettre à l’échelle les valeurs, pour chaque plan de couleur, afin de rendre l’apprentissage plus stable : \(\bar{x} = (x_R - \mu_R)/\sigma_R\)

Données non matricielles

Si une image est structurellement très proche d’un tenseur, il n’en est pas de même pour toutes les sources de données :

• Graphe : On peut par exemple utiliser un graphe pour modéliser un réseau social : les nœuds représentent les utilisateurs et les arêtes leurs relations. Ici, la structure est très éloignée d’une matrice. Pourtant, il est possible de modéliser ce graphe à l’aide d’une matrice d’adjacence, où \(M_{ij} = 1\) s’il existe une arête reliant le nœud i au nœud j.

• Nuage de points : Données récupérées par un LIDAR pour la conduite automobile, ce type de structure discrète reste difficile à injecter directement dans un réseau de neurones. Il est alors nécessaire de passer par des transformations intermédiaires, telles que la voxelisation ou des projections 2D, afin de produire des représentations assimilables à des images.

• Échantillonnage irrégulier : Les données acquises avec des intervalles de temps irréguliers ne peuvent pas être représentées dans une grille. Il faut alors adopter d’autres stratégies, comme encoder explicitement le temps \(t\) correspondant à la réception de l’information. On peut aussi interpoler l’information afin de simuler une donnée continue.

La réponse

En sortie du réseau, on obtient une information matricielle contenant des valeurs numériques. Pour certaines applications, ces valeurs correspondent directement aux éléments recherchés :

• Régression : Cette problématique consiste à prédire une ou plusieurs valeurs continues, comme un prix, une température ou une position.

• Génération : À partir d’une entrée (par exemple du texte), le réseau produit un contenu de sortie, comme une image. Ce principe est notamment utilisé dans des modèles de génération d’images.

• Détection : Dans une image, on cherche à localiser des objets d’intérêt. En sortie, le réseau fournit les coordonnées d’un rectangle englobant, sous la forme : centre, dimensions et score de confiance (par exemple dans les architectures de type YOLO).

En revanche, pour d’autres types de problèmes, il est nécessaire de construire une étape supplémentaire afin d’adapter la sortie du réseau à la problématique considérée. Voici quelques exemples :

• Détections multiples : Si l’on cherche à détecter plusieurs objets sur une même image, il faudrait idéalement que le réseau puisse générer une liste de zones d’intérêt. Or, la sortie d’un réseau de neurones est de taille fixe. Pour contourner cette contrainte, on fixe un nombre maximal de prédictions, par exemple 100 et ainsi le réseau va fournir toujours 100 zones d’intérêt de la forme \((x_i, y_i, L_i, H_i, score_i)\). Pour ne sélectionner que les prédictions valables, on conserve celles dont le score est supérieur à un certain seuil. On aurait pu choisir une approche différente en demandant au réseau de donner uniquement les éléments d’intérêt ainsi que leur nombre. Mais cette tâche s’avère bien plus difficile en pratique pour un gain inexistant.

  

• Classification : On cherche par exemple à déterminer à quel animal correspond une image. En supposant que nous traitions 100 animaux différents, nous allons faire en sorte que le réseau produise en sortie un vecteur de 100 valeurs, correspondant chacune à une sorte de score/probabilité pour chaque classe. La prédiction finale est obtenue en calculant l’argmax du tenseur 1D.

  

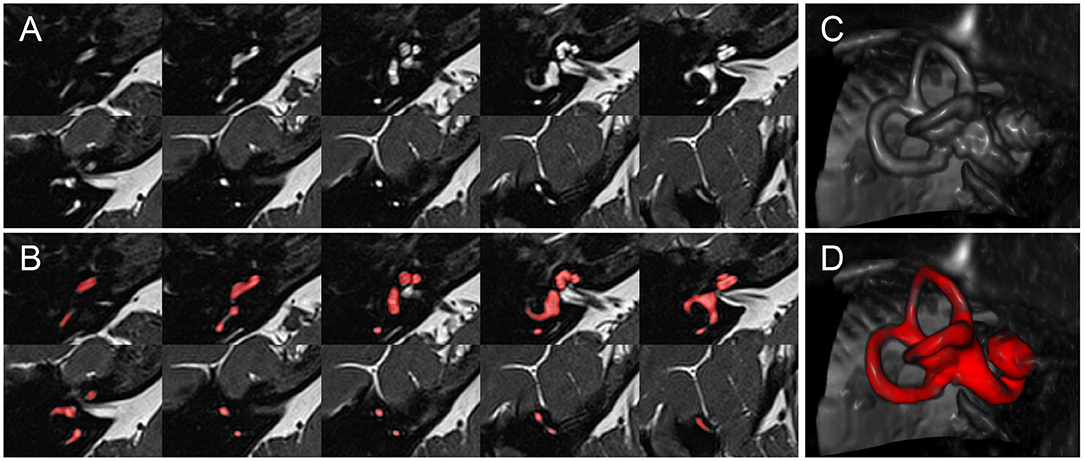
• Segmentation : On cherche ici à détecter un élément dans une image 2D ou 3D. Prenons l’exemple d’une IRM du cerveau dans laquelle on souhaite localiser l’oreille interne. L’objectif est d’obtenir un masque de valeurs 0/1 indiquant les voxels appartenant à l’oreille interne. Pour cela, le réseau produit en sortie un tenseur 3D de mêmes dimensions que l’IRM d’origine. Ces valeurs, sous forme de nombres réels, sont ensuite seuillées (par exemple à 0.5) afin de construire le masque final.

  

Conclusion

L’IA = une fonction mathématique

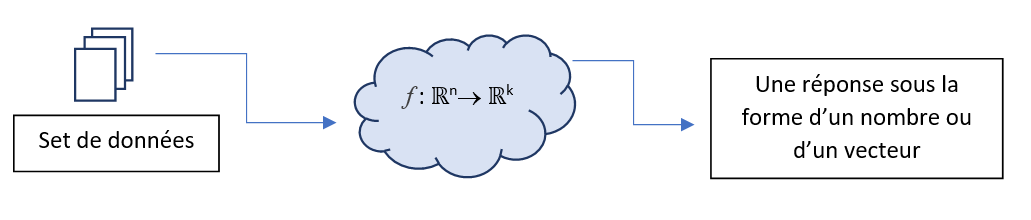
Nous avons vu que les informations manipulées en entrée et en sortie sont représentées sous forme de nombres stockés dans des tenseurs de différentes dimensions (1D, 2D, 3D, 4D, etc.). D’un point de vue abstrait, tout tenseur peut être considéré comme équivalent à un tenseur unidimensionnel contenant le même nombre d’éléments, indépendamment de sa structure initiale. En conclusion, concevoir une intelligence artificielle traitant \(n\) valeurs numériques en entrée pour produire \(𝑘\) valeurs numériques en sortie revient à définir une fonction mathématique \(f\) de \(\mathbb{R}^n\rightarrow \mathbb{R}^k\).

Voici donc notre premier système :