Les optimiseurs
Nous avons présenté la méthode de descente du gradient (gradient descent) utilisée pour minimiser l’erreur durant l’apprentissage. Il s’agit de la méthode historique : conceptuellement simple, facile à comprendre et implémentable en quelques lignes. Avec le temps, de nombreuses variantes ont été proposées afin de :
Corriger certaines limites des méthodes précédentes
Accélérer la convergence
Rendre l’apprentissage plus stable
Ces améliorations reposent sur des outils mathématiques de plus en plus sophistiqués. En pratique, ces méthodes sont directement mises à disposition dans les bibliothèques de deep learning dans la catégorie optimiseurs (optimizers).
Dans ce chapitre, nous présentons les approches principales que vous utiliserez le plus souvent en pratique.
Les optimiseurs classiques
Descente du gradient
La descente du gradient (Gradient Descent) classique utilise un pas fixe, aussi appelé learning rate. Le gradient de la fonction d’erreur totale est calculé à partir de l’erreur produite par l’ensemble des échantillons. Les paramètres du réseau sont ensuite mis à jour dans la direction opposée au gradient de la fonction d’erreur :
Avantages :
Méthode simple à comprendre
Formulation mathématique directe
Inconvénient :
Le calcul du gradient sur l’ensemble du jeu de données fait que chaque itération devient très longue
En pratique, cette méthode est rarement utilisée telle quelle. Par exemple, une epoch (traitement de l’ensemble des échantillons) peut prendre sur une base d’un million d’images plusieurs heures de calcul sur un GPU grand public.
Gradient stochastique et mini-batch
Voulant abandonner le calcul exact du gradient sur l’ensemble du DataSet, apparaît la méthode du Stochastic Gradient Descent (SGD) qui tire au hasard (stochastique) un seul échantillon dans la base afin de construire une estimation du gradient. Bien sûr, avec un seul échantillon, cette évaluation sera de mauvaise qualité et la courbe d’apprentissage deviendra trop bruitée.
En conséquence, on n’utilise pas la méthode SGD en pratique. Elle a toutefois posé les bases de la stratégie courament utilisée aujourd’hui et appelée mini-batch gradient descent :
En début d’epoch, on mélange le dataset (shuffle)
On découpe virtuellement le dataset en lot de taille égale : les mini-batchs.
On traite itérativement chaque mini-batch pour estimer le gradient et appliquer une descente
Lorsque l’on a traité tous les lots, l’epoch est terminée, on passe à l’epoch suivante
Avantages :
Mises à jour plus fréquentes => convergence généralement plus rapide.
Chaque échantillon est utilisé une fois et une seule fois par epoch
Inconvénients :
Le gradient est plus ou moins bruité en fonction de la taille des batchs choisie
Le mini-batch offre en pratique un compromis efficace entre stabilité et rapidité.
Bien que le mini-batch gradient descent constitue une base solide, il présente encore des limites en termes de stabilité et de vitesse de convergence. Les optimiseurs tels que Momentum ou Adam ont été introduits pour améliorer ces aspects.
Momentum
Afin de réduire le bruit du gradient et d’accélérer la convergence, on introduit un mécanisme appelé momentum. Le momentum ne constitue pas un algorithme d’optimisation à part entière, mais un terme d’inertie ajouté à la formule de descente de gradient. On va donc associer ce mécanisme à un autre algorithme comme le mini-batch gradient descent.
L’idée consiste à ne pas utiliser uniquement le gradient courant, mais à le pondérer avec une partie des gradients passés afin de lisser les changements trop bruités lors de l’optimisation.
Pour cela, on introduit un paramètre supplémentaire \(\gamma \in [0,1[\) contrôle l’importance accordée aux gradients passés ainsi qu’une variable auxiliaire notée \(V\) :
La mise à jour des paramètres du réseau s’effectue alors selon :
Avantage :
La technique du Momentum réduit les oscillations et améliore la stabilité de la convergence mais peut la ralentir.
Optimiseur adaptatif : Adam
Présentation
L’optimiseur Adam combine plusieurs idées introduites précédemment :
Estimation adaptative du pas pour chaque poids dans W
Prise en compte du momentum
Adam est aujourd’hui largement utilisé car
Il converge rapidement
Il nécessite peu de réglages
Il fonctionne correctement dans la majorité des cas
En pratique, Adam constitue un excellent choix par défaut pour entraîner un réseau de neurones.
Budget matériel
Avertissement
La performance, l’adaptibilité et la fiabilité de l’opérateur Adams, ce n’est pas gratuit ! En effet, en écrivant « Estimation adaptative du pas pour chaque poids dans W », cela implique que pour chaque poids dans le réseau, Adam maintient 2 float en plus du poids pour stocker l’estimation en question.
Et alors ? Et bien, cela fait mal. Prenons l’exemple de GPT-3, qui contient environ 175 milliards de paramètres. Si l’optimiseur Adam est utilisé pour l’apprentissage, quatre valeurs en tout doivent être stockées pour chaque poids :
Le poids
Le gradient
Les deux moments de l’optimiseur Adam
En utilisant une représentation en float32 (4 octets par valeur), cela représente :
de mémoire (ouille). La taille des données du mini-batch sont estimées pour GPT3 à 3 millions de tokens ce qui fait 12 Mo ce qui reste négligeable par rapport au reste.
L’entraînement de GPT3 a utilisé des GPU NVIDIA V100 disposant de 32 Go de mémoire. Il faut donc environ 90 GPU pour stocker le modèle, le gradient et l’optimiseur. A sa sortie, le prix d’une carte V100 avoisiné les 30 000 $. On obtient donc un coût matériel minimal d’environ :
Ce chiffre correspond uniquement au stockage en mémoire du modèle et de l’optimiseur ; il ne tient compte ni de l’électricité, ni de l’infrastructure réseau, ni des coûts humains. Les estimations publiques du coût total de calcul pour l’entraînement de GPT-3 se situent autour de 5 millions de dollars. On constate ainsi que ce simple raisonnement par ordre de grandeur permet d’aboutir à une estimation cohérente, illustrant le coût réel de l’entraînement de ce très grand modèle déjà ancient !
Quel optimiseur choisir ?
Pour un problème donné, le graphique ci-dessous présente les performances des différents optimiseurs :
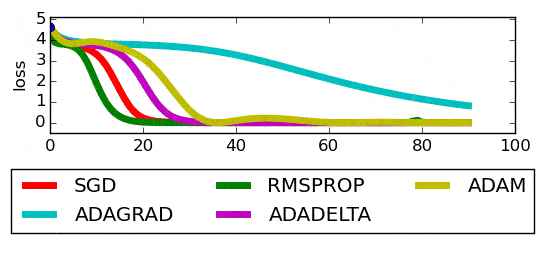
A partir de cet exemple, il ne faut jamais conclure qu’il existe un optimiseur universellement meilleur. Si l’on constate qu’un optimiseur « bat » les autres, cette conclusion est uniquement valable pour ce problème avec ces données.
En pratique, on peut retenir les recommandations suivantes :
Utiliser Gradient Descent pour tester rapidement et voir si tout fonctionne
Utiliser Adam comme choix par défaut fiable et efficace
Utiliser mini-batch + momentum pour un contrôle fin de l’apprentissage
L’optimisation reste en grande partie empirique : lorsque un optimiseur permet d’obtenir une convergence satisfaisante, l’objectif principal est atteint.
Quizzz
Si l’on prend des échantillons au hasard dans la base, l’algorithme de gradient descent est dit stochastique.
Le learning rate est optimal lorsque sa valeur est proche de 1.
L’approche Gradient Descent fonctionne mais elle reste plus lente.
L’optimiseur Adam consomme moins de mémoire que les poids du réseau.
Le paramètre de Momentum permet de lisser l’évaluation du gradient d’une itération à l’autre.
Si je dois choisir un optimiseur fiable et efficace sans paramètre à régler, je choisis SGD.
Le facteur de learning rate correspond au pas dans les méthodes de descente gradient.