L’apprentissage
La question légitime qui interpelle tout élève est la suivante : comment une machine peut-elle apprendre ? Nous allons répondre à cette question dans ce chapitre et présenter quelques notions clés utilisées dans l’apprentissage supervisé.
Les paramètres d’apprentissage
Dans le chapitre précédent, nous avons montré qu’une IA peut s’apparenter à une fonction mathématique \(f\). Cependant, pour pouvoir « apprendre », il faut que cette fonction puisse « évoluer » en s’améliorant si possible. Pour cela, nous ajoutons des paramètres supplémentaires, dits paramètres internes ou paramètres d’apprentissage ou encore poids (weights en anglais). Ces valeurs vont être utilisées comme des entrées supplémentaires de la fonction \(f\) au même titre que les données à traiter. Ainsi, nous obtenons le système suivant :
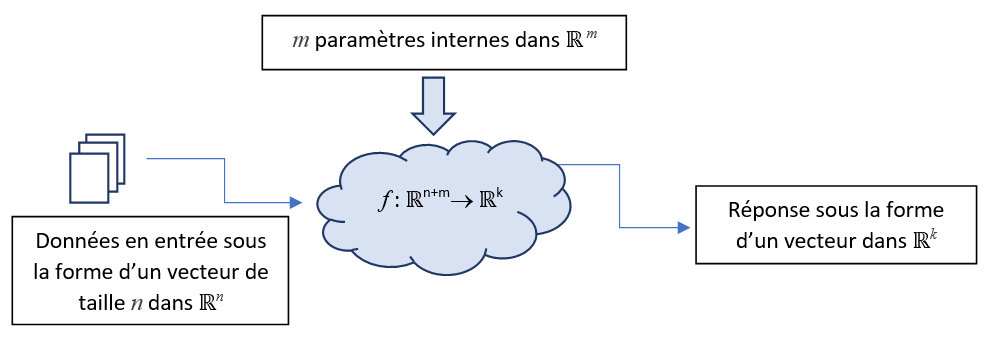
L’ajout de ces poids va permettre à notre système d’apprendre, en effet, si les réponses fournies par la fonction f sont incorrectes, on peut maintenant faire évoluer ces paramètres internes pour tenter d’obtenir une meilleure réponse.
Durant la phase d’apprentissage, il faut distinguer :
Les données en entrée qui doivent être vues comme des données « constantes » au sens où elles n’évoluent pas.
Les paramètres internes qui sont modifiés de manière itérative pour améliorer les performances de l’IA
Comment initialiser les paramètres internes en début d’apprentissage ? Impossible de répondre à cette question. Les paramètres sont donc initialisés aléatoirement par convention. De cette façon, en relançant un apprentissage, on démarre avec une « seed » différente.
L’apprentissage supervisé
Nous disposons d’une fonction pouvant apprendre, mais comment la guider ? L’approche la plus courante aujourd’hui s’appelle l’apprentissage supervisé qui consiste pour chaque échantillon en entrée à connaître la réponse exacte associée.
Par exemple :
Pour l’évaluation de l’âge d’une personne à partir d’une photo, nous connaissons pour chaque image l’âge exact de la personne.
Pour la classification d’images, on dispose d’une base d’images ainsi que la catégorie associée à chaque image : chien, chat, grenouille…
Pour la description automatique d’images : on dispose d’une phrase décrivant le contenu de chaque image.
Pour la transcription automatique (Speech to Text), plusieurs phrases enregistrées à l’oral constituent la base d’apprentissage et pour chacune d’entre elles, nous connaissons sa transcription.
L’apprentissage supervisé, pour être efficace, doit disposer de plusieurs milliers d’échantillons en entrée. Plus le nombre d’échantillons est important, plus la qualité de l’apprentissage augmente.
On peut citer quelques bases annotées utilisées régulièrement dans la formation et la recherche :
CIFAR10 : base d’images pour la classification d’images. 60 000 images, résolution de 32x32 en couleur, 10 classes : avion, voiture, oiseau, chat, daim, chien, grenouille, cheval, navire et camion.
CIFAR100 : 100 classes cette fois et 600 images par classe.
OXFOR102 : 102 classes de fleurs !
Fashion MNIST images en niveaux de gris de vêtements et autres articles de Zalando en 28x28.
FOOD 101 101 catégories de plats, 1000 images/classe.
FGVC Aircraft 102 catégories, 10 000 images.
Birdsnap 500 espèces d’oiseaux, 100 images par catégories.
ImageNet : base d’images qui sert de référence pour le problème de classification : 1000 classes, plus d’un million d’images en couleur de taille variable.
COCO : base d’images pour la segmentation et la description d’images : 80 000 images accompagnées de leurs descriptions.
Note
L’apprentissage non supervisé est une thématique de recherche consistant à catégoriser, par exemple, des photos d’animaux sans connaissance a priori des espèces présentes sur les images.
La fonction d’erreur
Lorsque le système nous fournit une estimation, nous pouvons évaluer sa qualité en utilisant une fonction d’erreur notée \(Err()\) permettant d’indiquer si l’estimation est éloignée de la réponse attendue. Par convention, la fonction d’erreur doit être positive et sa valeur doit augmenter lorsque la réponse s’éloigne de la valeur recherchée.
Prenons comme exemple le problème de l’estimation de l’âge d’une personne. En apprentissage supervisé, la base d’images contient pour chaque image, l’âge de référence noté : \(ref\). Notons \(est\) l’âge estimé par la fonction \(f\). Voici un exemple de fonction d’erreur que nous pouvons utiliser dans ce contexte :
Voici différents scénarios pour une personne de 37 ans :
Age estimé : 37, \(Err(37,37) = |37-37| = 0\) car on a trouvé la bonne réponse
Age estimé : 39, \(Err(37,39) = |37-39| = 2\) faible erreur, 2 ans trop vieux
Age estimé : 30, \(Err(37,30) = |37-30| = 7\) l’erreur augmente car l’écart augmente
Age estimé : 87, \(Err(37,87) = |37-87| = 40\) soit 40 ans trop vieux, l’erreur est forte
Nous constatons dans cet exemple que si l’erreur diminue, alors la qualité de la réponse augmente et réciproquement.
Note
Dans cet exemple, la valeur de l’erreur correspond à un nombre d’années. Mais rarement l’erreur aura une unité. Ainsi, dans le cas général, nous ne saurons pas si 0.1 ou 150 est associé à une erreur importante ou non.
L’erreur d’un échantillon
Prenons un échantillon dans notre base d’apprentissage. Nous utilisons la fonction \(f\) pour obtenir une estimation et nous injectons cette réponse directement dans la fonction d’erreur \(Err()\) pour obtenir une évaluation de sa qualité :
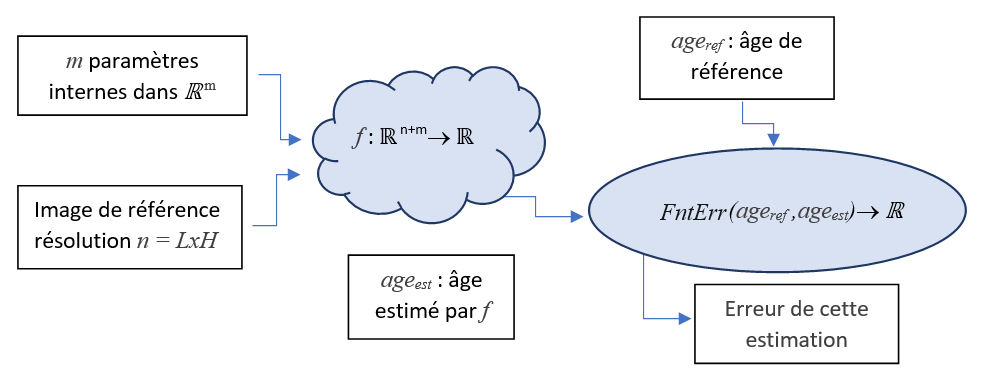
On peut donc construire une nouvelle fonction \(ErrEch()\) qui à partir d’un échantillon \(I\) donne directement l’erreur associée à cet échantillon :
Avec :
\(I\) : donnée en entrée (une image par exemple)
\(ref_I\) : réponse de référence associée à l’échantillon \(I\)
\(f\) : fonction d’apprentissage
\(W\) : paramètres d’apprentissage (weights)
L’erreur totale
Pour estimer l’erreur totale sur l’ensemble des échantillons de la base d’apprentissage, il suffit de sommer les erreurs associées à chaque échantillon :
Nous remarquons que :
L’erreur totale est une fonction qui dépend uniquement des poids W associés au réseau.
La fonction est à valeurs dans \(\mathbb{R}\)
Par conséquent, le problème d’apprentissage équivaut à minimiser l’erreur totale. Il peut donc se réécrire comme un problème d’optimisation :
On reconnaît ici un problème d’optimisation classique : la recherche du minimum d’une fonction.
Algorithme naïf
A ce niveau, nous pouvons déjà fournir un algorithme d’apprentissage ulta-naïf.
Nous tirons aléatoirement des poids W”
Si l’erreur totale associée à ces nouveaux poids est meilleure
Alors nous mettons à jour les poids W
Function OptimNaif(DataSet) :
ErreurMin = +∞
Tant qu’il reste du temps :
# on génère aléatoirement des poids W’
pour i allant de 0 à len(W) :
W’[i] = random.uniform(-1,1)
Erreur = ErrTot(W')
# si l'erreur est plus faible, on conserve les nouveaux poids W'
Si Erreur < ErreurMin :
W = W’
ErreurMin = Erreur
Ainsi, en itérant, on arrive à diminuer l’erreur, l’apprentissage est opérationnel !
La méthode du gradient
Dans le cours d’optimisation, vous avez vu que l’on peut itérativement améliorer les poids \(W\) pour réduire l’erreur totale en utilisant la méthode du gradient. Ainsi, à l’itération i, on applique la formule suivante :
Où
La valeur \(pas\) représente une valeur réelle
\(\nabla ErrTot\) représente le gradient de la fonction \(ErrTot\)
Notons \([w_0,w_1,...,w_{m-1}]\) les \(m\) paramètres internes dans \(W\). Nous rappelons que le gradient correspond aux dérivées partielles de la fonction \(ErrTot\) par rapport à chaque paramètre interne \(w_i\) :
La méthode du gradient nous garantit qu’avec un pas suffisamment petit, on diminue l’erreur totale à chaque itération.
L’optimum
Nous cherchons à minimiser la fonction \(ErrTot\) par rapport aux paramètres internes \(W\). En utilisant la méthode du gradient, nous descendons le long d’une pente à chaque itération. Nous finissons par atteindre un minimum local dans lequel l’algorithme va se mettre à osciller. Il est difficile de savoir à ce niveau comment sortir de cette zone pour trouver un meilleur optimum. On pourra relancer la phase d’apprentissage à partir d’une autre position de départ pour espérer trouver un meilleur optimum.
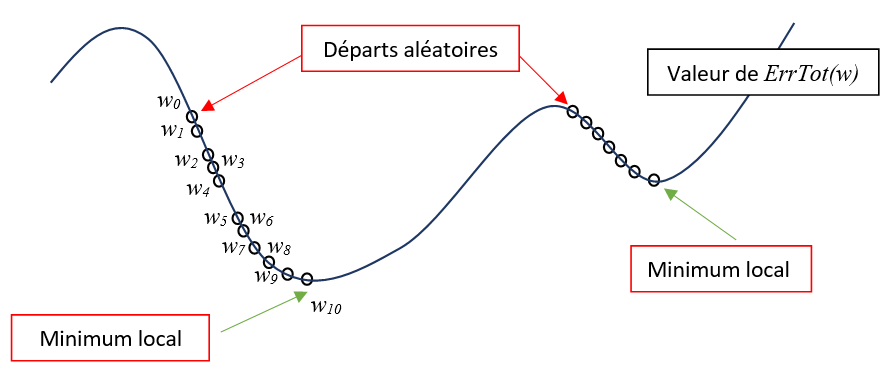
Ainsi, aucune méthode d’optimisation ne peut garantir la convergence vers l’erreur minimale. En effet, il nous est impossible de déterminer un fois un minimum atteint, s’il s’agit d’un minimum local ou d’un minimum global.
Les écueils de l’apprentissage
Voici les différents écueils que vous pouvez rencontrer lors de la mise en place d’une méthode d’apprentissage :
La non convergence : une phase d’apprentissage peut ne pas converger ! En effet, il se peut que la courbe de l’erreur oscille fortement à chaque itération montrant que les poids trouvés sont associés à un apprentissage instable.
Le succès minimal : il ne faut pas se laisser impressionner par un taux élevé de bonnes réponses pris isolément. Par exemple, un système qui prédit le sexe d’une personne avec un taux de réussite de 60% ne fait en réalité que 10 % de mieux qu’une prédiction aléatoire, dont la performance de référence est de 50%.
L’évidence : dans des situations évidentes, l’apprentissage va chercher la voie la plus simple ! Par exemple, pour classifier des images de grenouilles, de dauphins et de lions, très rapidement le réseau va atteindre 100% de prédictions correctes, même en utilisant 1 seul neurone ! En effet, pour produire une bonne réponse, le réseau n’a pas besoin de déterminer la nature du sujet photographié car il lui suffit d’analyser la teinte moyenne de l’image pour classifier facilement ces trois catégories :
vert pour la catégorie grenouille
jaune pour la catégorie lion
bleu pour la catégorie dauphin
Des ensembles déséquilibrés : si vous cherchez à classifier des images de chats et de chiens et que vous fournissez 1000 photos de chats et 10 photos de chiens, l’apprentissage va atteindre 99% de bonnes réponses très rapidement. Pour cela, il suffit au réseau de répondre toujours « chat » ce qui donne immédiatement 99% de réussite. Ce comportement vient du fait que vous avez une majorité de photos de chats dans votre base.
Note
Lorsque vous manquez d’échantillons pour votre apprentissage, une technique consiste à utiliser de la data augmentation pour simuler des données supplémentaires. On peut par exemple créer des images à partir de légères translations et rotations des images d’origine. On peut aussi ajouter du bruit ou des tâches dans l’image d’origine pour rendre la prédiction plus robuste aux perturbations.
Exercices
Les paramètres à conserver en production
L’apprentissage comporte deux phases distinctes :
La phase d’apprentissage consiste, à partir d’une base de vérités terrains, à faire évoluer les paramètres internes afin de minimiser l’erreur totale.
Une phase d’exploitation où les paramètres internes sont maintenant figés. Le système se comporte comme un expert auquel on présente de nouvelles informations pour connaître sa réponse.
Que doit-on conserver comme information une fois la phase d’apprentissage terminée ? Ces informations doivent être suffisantes pour traiter de nouvelles données (phase d’exploitation).
Les images contenues dans la base d’apprentissage |
|
La fonction \(f\) |
|
La fonction d’erreur |
|
Les réponses contenues dans la base |
|
La méthode d’optimisation |
|
Les paramètres internes de \(f\) |
Compréhension et mots-clefs
La fonction d’erreur peut donner des valeurs dans \(\mathbb{R}^3\).
La fonction \(f\) est toujours une fonction à valeur dans \(\mathbb{R}\).
Dans le processus d’apprentissage, la fonction d’erreur est optionnelle.
Les poids et le gradient contiennent autant d’éléments.
L’erreur totale correspond à la somme des erreurs depuis le début de l’apprentissage.
Différentes séquences d’apprentissage finissent toujours par converger vers des poids identiques.
Pour apprendre, la fonction \(f\) utilise des paramètres internes.
Pour l’apprentissage, l’utilisation d’une fonction d’erreur est optionnelle.
L’apprentissage supervisé consiste à vérifier que l’erreur diminue tout au long du processus d’apprentissage.
Le monitoring de l’apprentissage
Durant l’apprentissage, le modèle ajuste ses paramètres en minimisant l’erreur totale. L’évolution de cette quantité peut être représentée graphiquement sous la forme d’une courbe appelée training loss. L’analyse de cette courbe permet notamment de vérifier :
si l’erreur totale diminue → l’optmisation se passe correctement
si la décroissance est régulière au fil des itérations → suggère une convergence vers un minimum
si l’erreur oscille ou diverge → gradient trop élevé ou une instabilité de l’optimisation
En parallèle, il est courant d’évaluer l’erreur totale sur un jeu de données distinct, non utilisé dans l’apprentissage. Ces données constituent le jeu de validation, et la courbe correspondante est appelée validation loss. Dans une situation idéale, les courbes de training loss et de validation loss présentent des évolutions similaires :
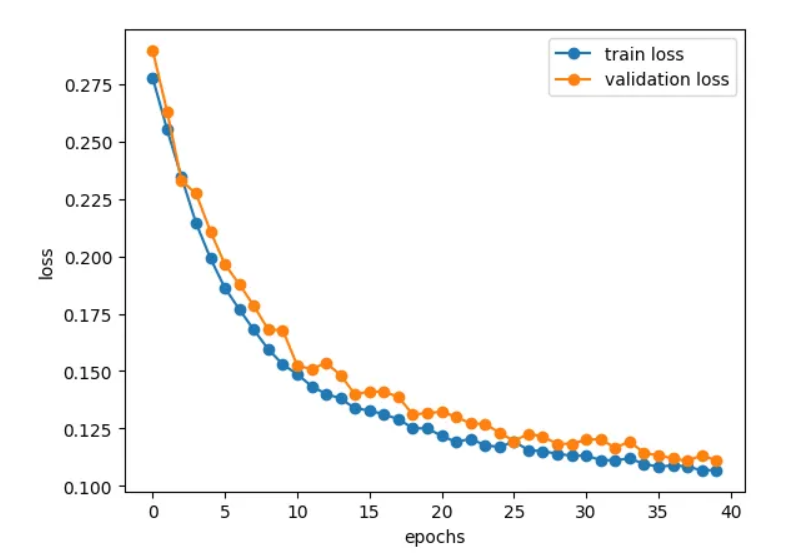
Lorsque la training loss continue de diminuer tandis que la validation loss cesse de décroître ou augmente, on observe un phénomène de surapprentissage : le modèle apprend alors de manière excessive les données d’entraînement, au point de mémoriser les réponses associées aux échantillons. Le réseau est alors capable de fournir de très bonnes réponses sur les données du set d’apprentissage mais se trompe lorsqu’on lui présente de nouvelles données. On dit alors que le réseau généralise mal à de nouveaux échantillons.
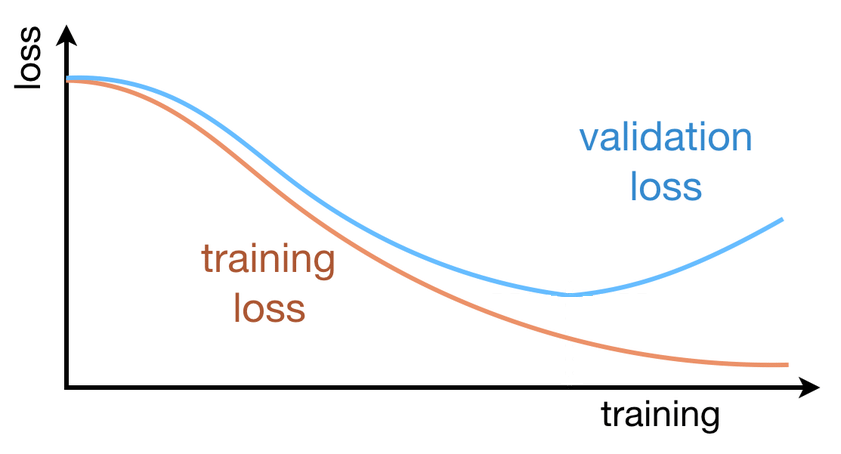
En début d’apprentissage, on surveille les courbes : validation loss et de train loss, car ces deux courbes indiquent si l’optimisation se déroule correctement et si le réseau « apprend » effectivement. En fin d’apprentissage, la performance du modèle est évaluée grâce à une autre mesure appelée accuracy (précision) correspondant au taux de bonnes réponses. L’accuracy répond à une question simple, mais essentielle : dans quelle proportion le modèle fournit-il une bonne réponse ? Exprimée sous forme de pourcentage, elle se comprend immédiatement et ne nécessite aucun bagage mathématique particulier ; elle est donc particulièrement adaptée pour communiquer des résultats. L’accuracy donne ainsi une évaluation globale des performances du modèle.
Comme pour la loss, l’accuracy est calculée à la fois sur le jeu de train ainsi que sur le jeu de validation. Nous présentons un exemple dans les courbes ci-dessous. Nous remarquons tout d’abord que les courbes d’accuracy sont inversées par rapport aux courbes de loss. En effet, les courbes de loss diminuent au fil des itérations pour idéalement tendre vers 0. Les courbes d’accuracy augmentent au fur et à mesure des itérations pour tendre idéalement vers 100%.
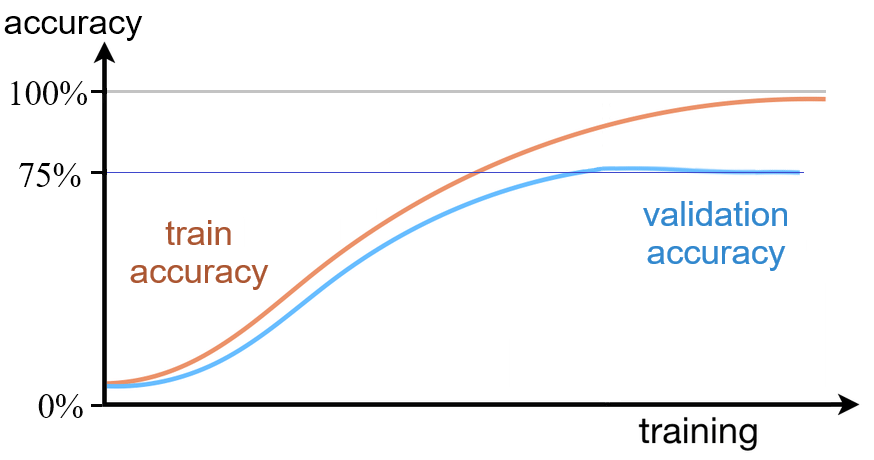
Les courbes de validation accuracy et de train accuracy permettent aussi de détecter le surapprentissage. Dans le graphique ci-dessus, on constate que la train accuracy continue à augmenter pour atteindre un quasi sans faute proche de 100% alors qu’à partir d’une certaine itération, la courbe de validation accuracy stagne et n’évolue plus. Les progrés obtenus sur le set de train ne se généralisent pas sur le set de validation, on est donc en présence d’un surapprentissage.
L’usage veut que l’on détecte plus facilement le surapprentissage sur les courbes de Loss car la divergence apparentrait plus tôt. L’apparition d’un décalage entre les deux courbes de train accuracy et de validation accuracy vient alors confirmer la présence du surapprentissage.
Lorsque vous effectuez plusieurs entraînements, si l’on doit classer les réseaux par performance, on le fera sur la courbe de validation accuracy car elle indique la performance réelle du réseau à la fin de l’entraînement. La courbe de Loss elle ne permet pas de comparer l’efficacité réelle des différents réseaux.
L’accuracy s’exprime sous la forme d’un pourcentage.
On détecte le surapprentissage lorsque l’erreur totale se met à osciller.
Les courbes de Loss diminuent vers 0 et les courbes d’accuracy croissent vers 100%.
La phase de validation consiste à présenter les données servant d’entraînement pour évaluer le taux de réussite.
Le surapprentissage se détecte lors de l’apparition d’un écart entre la courbe de validation loss et de validation accuracy.
On classe la performance de plusieurs réseaux en comparant leur train accuracy.
Les courbes de Loss diminuent vers 0 et les courbes d’accuracy croissent vers 100%.
On monitore 4 courbes durant l’apprentissage : validation loss, accuracy loss, validation train et accuracy train.
On peut détecter le surapprentissage grâce aux courbes de loss ou d’accuracy
Exercice
Apprentissage d’une fonction binaire
Nous cherchons à apprendre la fonction booléenne \(EstPositif(x)\) valant \(0\) si \(x < 0\) ou \(1\) sinon. Pour cela, on utilise les échantillons ci-dessous qui vont servir de référence pour l’apprentissage :
\(x_i\) |
\(Res_i\) |
|---|---|
-5 |
0 |
0.5 |
1 |
Nous choisissons comme fonction d’apprentissage :
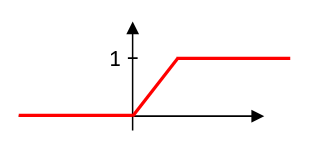
où \(x\) correspond à l’entrée et \(a\) au seul paramètre interne permettant l’apprentissage. Nous choisissons comme fonction d’erreur l’écart entre le résultat et la valeur de référence :
La prédiction \(f(-5,1)\) est-elle correcte ?
La prédiction \(f(0.5,1)\) est-elle correcte ?
Pour \(a=1\), calculez la valeur de l’erreur totale pour les échantillons donnés.
Pour \(a=1.2\), calculez la valeur de l’erreur totale pour les échantillons donnés.
En augmentant la valeur de \(a\) à la question précédente, l’erreur totale a-t-elle diminué ?`
Comme prochaine valeur de \(a\), vaut-il mieux tester \(1.4\) ou \(0.8\) ?
Pour \(a=4\), l’erreur totale est nulle. La fonction \(f(x,4)\) correspond-t-elle à la fonction \(EstPositif(x)\) ?