Les réseaux convolutionnels
Dans ce chapitre, nous présentons les réseaux convolutionnels (Convolutional Neural Networks – CNN), une famille particulière de réseaux de neurones. Un réseau est qualifié de convolutionnel dès lors que son architecture comporte au moins une couche de type Convolution. Historiquement, l’introduction de ces couches a constitué une avancée décisive, permettant aux réseaux de neurones de franchir un cap majeur en termes de performance.
La couche Conv2D
Principe
Considérons le cas d’une image en niveau de gris se modélisant sous la forme d’un tableau 2D. Pour calculer le résultat d’une convolution 2D, nous avons besoin :
D’un tableau de taille (H,W) représentant l’image
D’un noyau de taille (u,v)
La résultat de la convolution sera un tableau 2D construit de la façon suivante :
On considère toutes les sous-images de taille (u,v) dans l’image d’origine
Pour chaque sous-image : on calcule sa convolution avec le noyau
On assemble les valeurs issues des convolutions pour former le tenseur de sortie
La sous-image et le noyau ayant même taille, la convolution entre ces deux tableaux ca consister à effectuer une multiplication membre à membre suivie d’une sommation des valeurs.
On peut extraire H-u+1 sous-images dans la hauteur et W-v+1 sous-images dans la largeur, ainsi, le tenseur de sortie aura une taille de (H-u+1, W-v+1).
En résumé, voici l’algorithme de la convolution 2D :
def ConvBase(TImage,Tnoyau) :
H,W = TImage.shape
u,v = Tnoyau.shape
# tableau résultat
Hr = H-u+1
Wr = W-v+1
sizeR =(Hr,Wr)
R = np.empty(sizeR)
# Calcul
for x in range(W):
for y in range(H):
sousImage = ExtractImage(TImage,x,y,u,v)
value = Conv(sousImage,Tnoyau) # multiplication membre à membre et sommation
R[x,y] = value
return R
Avec :
Voici un exemple utilisant une image 4x4 et un noyau 2x2 :
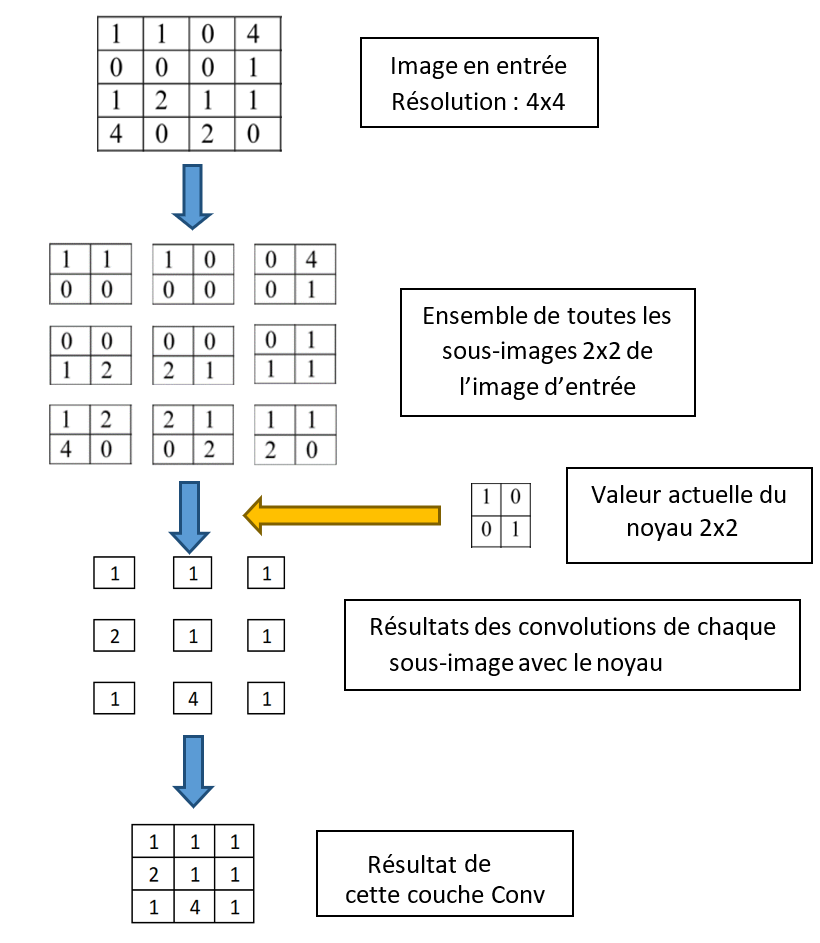
Note
Pour essayer de gagner en performance, on ne calcule pas la convolution en chaque point de l’image, mais seulement tous les k pixels. Ce saut est appelé pas ou stride. Il permet de réduire le temps de calcul et la taille du tenseur de sortie d’un facteur k².
Note
Pour éviter que la taille du tenseur en sortie rétrécisse à cause du terme en (H-u+1, W-v+1), on peut élargir virtuellement l’image d’entrée sur les bords en ajoutant des 0 grâce au paramètre de marge ou zero padding. Cette augmentation virtuelle de la taille de l’entrée permet d’obtenir une sortie de taille identique (H,W).
Gestion des canaux
Nous généralisons maintenant la convolution 2D aux cas des images avec plusieurs canaux. Dans ce contexte, on ajouter une dimension supplémentaire à l’image et au noyau pour avoir plusieurs canaux :
Une image (C,H,W)
Un noyau de taille (C,u,v)
Vous remarquez que pour représenter une image RVB dans un tableau, on utilise le mode Channels First où la première dimension correspond au canal des couleurs.
Comment gérer la convolution dans ce contexte ? On va traiter chaque couche indépendamment. Par exemple, pour une image RVB, on effectue 3 convolutions : la couche Rouge de l’image avec la couche Rouge du noyau, puis la verte, puis la bleu. Les 3 convolutions obtenues sont ensuite sommées pour former le résultat final. Voici l’algorithme de principe :
def ConvC(TImage,Tnoyau) :
C,H,W = TImage.shape
C,u,v = Tnoyau.shape
# tableau résultat :
size = (C,H-u+1, W-v+1)
R = np.zeros(size)
for i in range(1,Channels):
R += ConvBase(TImage[i],Tnoyau[i])
return R
Noyaux multiples
Le noyau présent dans une couche convolutionnelle permet de détecter et d’apprendre une caractéristique feature : un rond, un trait, une forme spécifique utile pour le problème considéré. Evidemment, il faut apprendre plusieurs caractéristiques pour produire une réponse de qualité ! Par conséquent une couche convolutionnelle va donc gérer plusieurs noyaux. Pour éviter d’ecrire une boucle pour traiter chaque noyau de la convolution, il est plus simple d’empiler les résultats produits par chacun des K noyaux dans un seul tenseur. Pour cela, il faut ajouter une dimension supplémentaire au tenseur des noyaux et au tenseur de sortie. Ainsi, nous avons :
Une image (C,H,W)
Un tenseur des noyaux : (K,C,u,v)
Un tenseur de sortie : (K,H',W')
Voici l’algorithme de principe :
def ConvNC(TImage,Tnoyaux) :
C,H,W = TImage.shape
K,C,u,v = Tnoyaux.shape
# tableau résultat :
size = (K,H-u+1, W-v+1)
R = np.empty(size)
for i in range(K):
R[i] = ConvC(TImage,Tnoyau[i])
return R
Série d’images
Pour terminer, nous rappelons que dans un réseau, on traite plusieurs images dans un seul batch. Pour éviter une boucle sur les images à traiter, il est plus simple d’ajouter une dimension supplémentaire dans le tenseur d’entrée permettant d’empiler les images dans un seul tableau. Ainsi, le tenseur représentant N images correspond à un tableau 4 dimensions (N,C,H,W). Dans la même logique, le tenseur de sortie gagne une dimension supplémentaire correspondant au nombre d’images : (N,K,H',W')
Ainsi, le tenseur de sortie est un empilement des résultats produits par chaque image :
def Conv2Dfinal(TImages,Tnoyaux) :
N,C,H,K = Timages.shape
K,C,u,v = Tnoyaux.shape
size = (N,K,H-u+1,W-v+1)
R = np.empty(size)
for i in range(N):
R[i] = ConvNC(TImages[i],Tnoyaux)
return R
En conclusion :
Pour une couche Conv2D traitant :
Un tenseur d’images de taille (N,C,H,W)
Un tenseur de noyaux de taille (K,C,u,v)
Avec :
N : nombre d’images
C : nombres de canaux
K : nombre de noyaux
La taille du tenseur en sortie de la couche Conv2D est : (N,K,H',W')
Avec H'=H-u+1 et W'=W-v+1.
Exemple
Pour 512 images RVB de résolution 256x256 avec une couche convolutionnelle apprenant 12 features de taille 5x5, le tenseur en sortie de cette couche convolutionnelle aura une taille (512,12,252,252).
Pour une couche Conv2D, le nombre de features s’appelle la profondeur de la couche Conv. Le pas, la marge et la profondeur de la couche CONV sont des hyperparamètres d’apprentissage du réseau : ils sont choisis par l’utilisateur en début d’apprentissage et n’évoluent pas durant l’apprentissage. La couche Conv participe aux calculs Forward du réseau et son résultat contribue à l’erreur finale. Ainsi les valeurs contenues dans ses noyaux correspondent à des poids qui vont ainsi être optimisés par la méthode du gradient.
Interprétation des features
Mais à quoi peuvent correspondre les features présents dans les noyaux, c’est une question difficile ! Cependant, on sait qu’au niveau de la couche d’entrée, ces features correspondent à des détecteurs de contours. Par exemple, voici les features appris pour le problème de la classification des chiffres manuscrits :

Exercices
Exercice 1
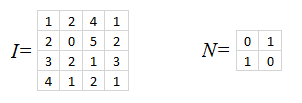
Exercice 2
Donnez la taille de la sortie d’une couche Conv2D en fonction des informations suivantes :
Entrée
Taille Noyaux
Sortie
(1,1,10,10)
(1,3,3)
(1,1,8,8)
(9,1,32,32)
(1,5,5)
(7,3,12,12)
(1,3,3)
(5,3,28,28)
(9,5,5)
La couche POOL
Objectif
L’objectif d’une couche Pool est de réduire la quantité d’informations qui transitent d’une couche à l’autre. Par exemple, pour un tableau 2D, on peut choisir de le diviser en blocs de taille 2x2 et d’effectuer pour chaque bloc une opération du type : moyennage, min ou max… Le tableau résultat aura donc une taille 4 fois moindre.
Nous présentons un exemple de MaxPool-2D avec une réduction 2x2 :

La couche DropOut
Cette couche permet de mettre à zéro aléatoirement certaines valeurs d’un tableau ceci avec une probabilité donnée. Il n’y a pas réduction de la taille des données, mais simplement une simulation d’une perte d’information. L’intérêt est d’améliorer l’indépendance entre les différents features. En effet, supposons que le réseau doive trouver deux features A et B. Sans la technique de DropOut, il pourrait aussi bien sélectionner les features A et A+B, car les traitements sur les couches suivantes pourraient reconstruire les features A et B idéaux. En désactivant de temps à autre le feature A ou B, cela force le réseau à converger sans tenir compte des valeurs des features voisins.
Les couches DropOut ne sont utiles que durant la phase d’apprentissage et non durant la phase de validation. Ainsi, elles seront activés durant la phase d’apprentissage et ignorées pendant la phase de validation.
On donne pour cette couche une probabilité p d’effacer une donnée. Cela sous-entend que la somme des valeurs en sortie est abaissée (en moyenne) d’un facteur 1-p par rapport à l’entrée. Pour compenser cette perte, un facteur 1/(1-p) est appliquée aux valeurs conservées pour préserver le niveau moyen des valeurs d’entrée. Voici un exemple de l’application d’une couche Dropout avec une probabilité de 0.5 sur un tableau rempli de valeurs 1. Vous remarquez que sur les 10 valeurs présentes 6 ont été mises aléatoirement à zéro. Les valeurs de sortie sont multipliées par 2 = 1/p pour compenser le niveau d’entrée. En relançant ce test, on obtient des résultats différents.
Input : tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
Output : tensor([0., 0., 0., 0., 2., 2., 0., 0., 2., 2.])
Lecture d’illustration
Etudions l’exemple suivant :
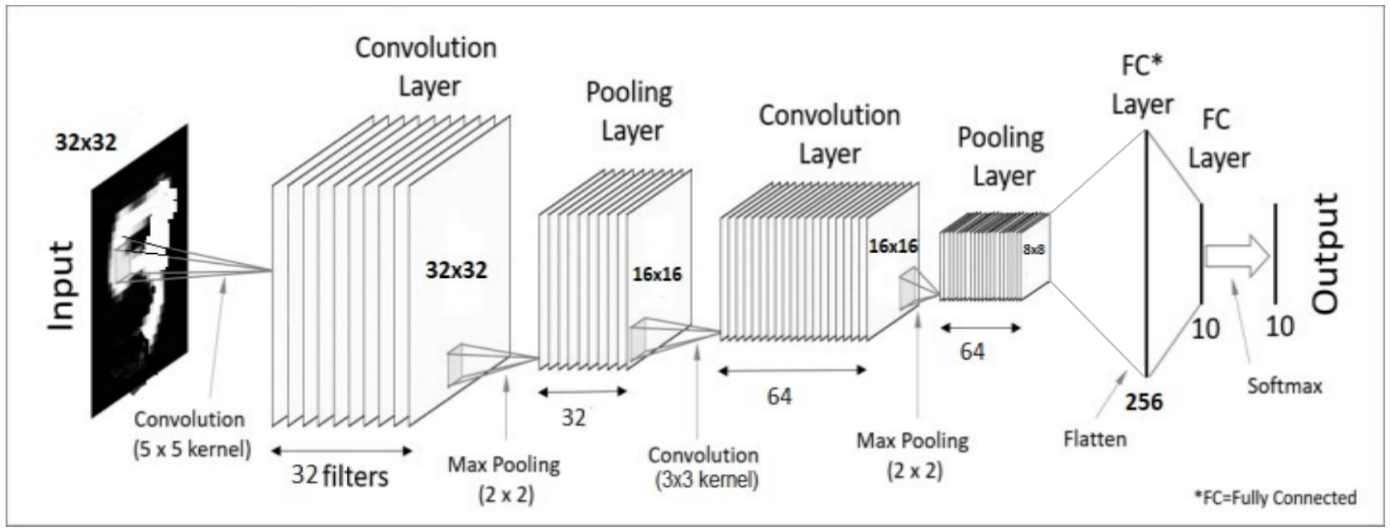
Nous analysons ce réseau de gauche à droite. Sur ce schéma, les tableaux en entrée/sortie des différentes couches sont représentés par des empilements de rectangle. Les opérations effectuées par chaque couche sont notées en bas des illustrations.
En entrée, on trouve une image 2D de résolution 32x32 en niveaux de gris.
La sortie de la première couche est le résultat d’une convolution 2D donnant un tableau de taille (32,32,32). Il y a donc 32 features dans cette couche Conv. Les features étant de taille 5x5, la résolution de sortie aurait dû être de 28x28 et non 32x32, un paramètre de zéro padding a dû être utilisé pour compenser la perte de résolution.
La couche de Max-Pooling réduit la résolution par 2, ce qui donne un tableau (32,16,16). Il y a toujours 32 canaux car l’opération de MaxPooling2D ne s’applique qu’aux deux premières dimensions.
Une nouvelle couche Conv de 64 features est appliquée. Le tableau d’entrée ayant une taille de (32,16,16), celui de sortie une taille de (64,16,16) et celui du noyau 3x3, le noyau de la couche Conv2D a été construit avec un tableau (64,32,3,3). Cette couche traite donc le tableau d’entrée comme une image 16x16 de 32 canaux.
La couche de Max-Pooling suivante réduit la résolution par 2, ce qui donne un tableau (64,8,8) en sortie. Le nombre de canaux reste inchangé.
Le tableau [64,8,8] subit un « flatten » pour être aplati sous la forme d’un tableau 1D de taille 64x8x8 = 4096.
On trouve ensuite une couche Linear (aussi appelée Fully Connected). La grandeur 256 indique sûrement le nombre de neurones présents dans cette couche. La fonction d’activation n’est pas précisée, on peut supposer qu’il s’agit d’une fonction ReLU. Chaque neurone de cette couche est connecté aux 4096 entrées de la couche précédente.
La dernière couche correspond à une deuxième couche Linear. Elle contient 10 neurones qui calculent 10 scores correspondant aux 10 catégories étudiées.
Pour finir, les valeurs obtenues étant quelconques, négatives comme positives, on applique la fonction Softmax qui transforment ces 10 valeurs en 10 probabilités de somme 100%.
Les deux parties d’un réseau
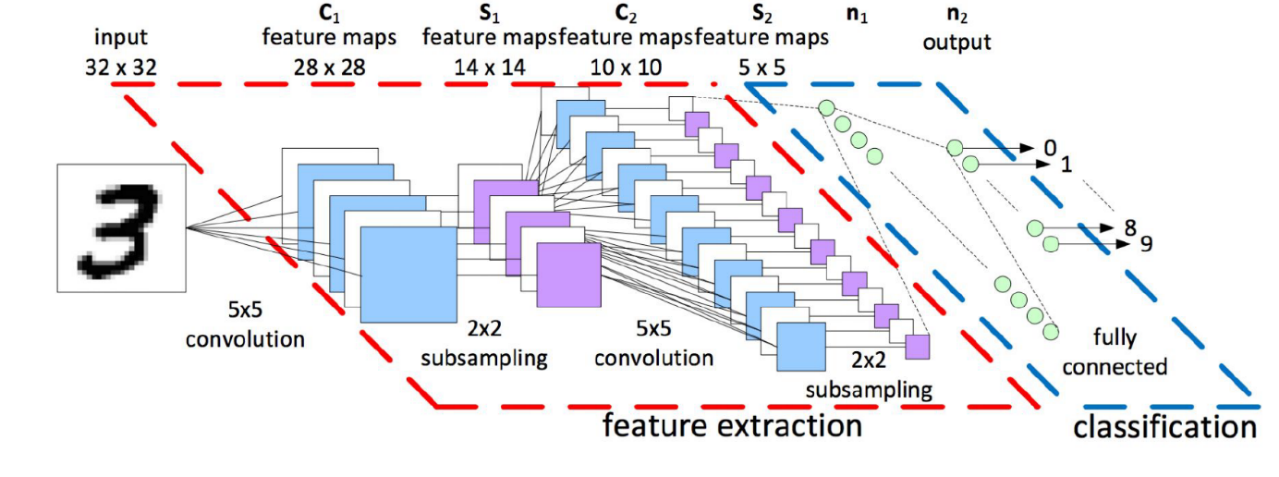
La partie gauche du réseau, proche de l’entrée, cherche à évaluer des features permettant à la partie droite du réseau de faciliter sa décision. Ainsi, les réseaux utilisés en classification d’images ont tendance à se séparer en deux parties :
La partie gauche, proche des données d’entrée, a pour objectif d’estimer et de trouver un ensemble de critères « feature extraction » ceci en empilant plusieurs couches Conv.
La partie droite doit construire sa réponse et apprendre à classifier l’image à partir des critères évalués par la partie gauche du réseau. Pour mettre en place cette partie, on utilise plusieurs couches Linear empilées.
On peut ainsi transférer des réseaux déjà entraînés vers d’autres problèmes. Par exemple pour un réseau entraîné sur la classification d’images, on peut reprendre ce réseau tel quel, garder sa partie gauche car on suppose qu’elle contient des détections de features dans une image et remettre à zéro la partie droite afin d’apprendre sur un nouveau set d’images spécialisées : bâtiments, bactéries, véhicules. Cela permet d’économiser un temps précieux d’apprentissage.