Les fonctions d’erreur

La réponse en sortie d’un réseau de neurones est généralement assez simple à interpréter, du moins dans ses grandes lignes :

Pour un problème de régression, la sortie correspond à la valeur prédite.

Pour un problème de classification, le score le plus élevé indique la classe retenue.

Pour un problème de segmentation d’images, un masque binaire (0/1) indique les pixels ou voxels retenus.

Pour un problème de détection, les coordonnées des rectangles dans l’image indiquent les zones d’intérêt.

En revanche, définir une fonction d’erreur adéquate à connecter à la sortie du réseau afin de permettre l’apprentissage reste une tâche délicate. À titre d’exemple, plusieurs fonctions de loss sont présentées dans ce chapitre.

Mean Squared Error

Cette fonction d’erreur calcule la moyenne des carrés des différences entre deux séries de valeurs. Ainsi, la MSE entre un vecteur \(r\) contenant des valeurs de référence et un vecteur \(e\) contenant les valeurs estimées est définie par :

\[\frac{1}{n} \cdot \sum_{i=0}^{n-1} (e_i - r_i)^2\]

Par exemple, avec r=[6, 1, 5, 3, 5] et e=[10, 1, 2, 3, 5], on obtient :

\[\begin{split}\begin{array}{c|c|c|c} r & 6 & 1& 5 & 3 & 5 \\ \hline e & 10 & 1& 2 & 3 & 5 \\ \hline |e_i-r_i| & 4 & 0& 3 & 0 & 0 \\ \hline carré & 16 & 0& 9 & 0 & 0 \\ \end{array}\end{split}\]

Ainsi la somme des carrés est égale à 25. Comme il y a 5 éléments, nous obtenons au final une MSE de 5.

Pour les valeurs suivantes, calculez l’erreur MSE associée :

[ 1, 2, 3, 4 ] et [ -1, 4, 5, 2 ]

Dice

Dans un problème de segmentation d’images 2D, la sortie du réseau de neurones est généralement un masque de probabilités, de même dimension que l’image d’entrée. Chaque pixel est associé à une probabilité d’appartenir à l’objet recherché dans l’image.

Coefficient de Dice

Pour simplifier, considérons deux masques binaires 2D, notés r (référence) et e (estimation) où chaque pixel prend la valeur 0 ou 1, la valeur 1 étant associée à la zone d’intérêt. La notation \(|r|\) correspond au nombre de pixels valant 1 dans le masque r. L’opération \(v=e\cap r\) est défini ainsi :

v(i,j) = 0 si r(i,j) = 0 ou e(i,j) = 0

v(i,j) = 1 si r(i,j) = 1 et e(i,j) = 1

Le coefficient de Dice est défini par :

\[\mathrm{Dice}(r, e) = \frac{2 \lvert r \cap e \rvert}{\lvert r \rvert + \lvert e \rvert}\]

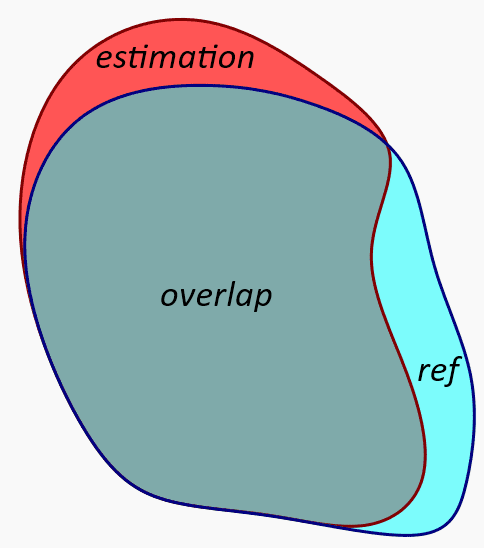
La valeur \(\mathrm{Dice}(r, e)\) mesure le taux de recouvrement (overlap) entre les deux ensembles de pixels. Elle vaut 1 lorsque les deux masques sont identiques, et 0 lorsqu’ils ne se recouvrent pas.

Dans le cas de masques probabilistes à valeurs dans [0,1] cette expression peut s’écrire sous la forme suivante :

\[\mathrm{Dice}(r, e) = \frac{2 \sum_i r_i.e_i}{\sum_i r_i + \sum_i e_i}\]

Fonction DiceLoss

Dans le cadre de l’apprentissage automatique, on convertit cette mesure de similarité en une fonction de perte à minimiser, appelée Dice loss :

\[\mathrm{DiceLoss}(r, e) = 1 - \mathrm{Dice}(r, e)\]

En pratique, les sorties du réseau prennent des valeurs continues dans l’intervalle \([0,1]\) et la référence est un masque binaire à valeurs dans {0,1}. Dans ce contexte, le coefficient de Dice est bien défini et permet au réseau d’apprendre la forme de référence.

Cette fonction d’erreur favorise directement un bon recouvrement global des objets, ce qui la rend particulièrement adaptée aux tâches de segmentation d’images.

La fonction Dice Loss est utilisée principalement dans les problèmes de segmentation d’images.

Si le Dice vaut 0.5 avec |r|=|e|, alors cela veut dire que le recouvrement est de 50%.

Si le Dice vaut 1 alors les deux surfaces sont séparées.

Cross Entropy

Softmax

Dans le problème de la classification d’images, le réseau de neurones associe à une image plusieurs valeurs réelles correspondant à une sorte de score pour chaque catégorie étudiée. Il est naturel de supposer qu’une valeur supérieure aux autres correspond à une catégorie plus probable. Mais comment interpréter des valeurs négatives ou nulles ? Pour cela, nous utilisons la fonction Softmax qui permet de transformer toute série de valeurs \(X=(x_j)_{0\le j<n}\) en une distribution de probabilités. La i-ème composante du vecteur \(Softmax(X)\) est définie ainsi :

\[Softmax\left(X\right)_i = \frac{\exp(x_i)}{\sum_{j=0}^{n-1}{\exp(x_j)}}\]

Questions :

Justifiez que les valeurs obtenues par la fonction Softmax() sont dans l’intervalle [0,1]

Vérifiez que leur somme est égale à 1

Voici un exemple :

\[\begin{split}\begin{array}{c|c|c|c}& Input & exp(x_i) & Total & exp(x_i)/Total\\ \hline x_0 & -1 & 0,368 & & 1,59\% \\ x_1 & 1 & 2,718 & 23,172 & 11,73\% \\ x_2 & 3 & 20,08 & & 86,68\% \\ \hline \end{array}\end{split}\]

Nous pouvons remarquer deux propriétés intéressantes :

Croissance : si une valeur en sortie du réseau augmente alors la probabilité correspondante en sortie de la fonction Softmax augmente aussi

Stabilité : si les valeurs en sortie du réseau se translatent d’une constante, les probabilités sont inchangées

Pour le tenseur d’entrée suivant, calculez les probabilités obtenues en sortie grâce à l’application de la fonction Softmax. Donnez les valeurs en pourcent avec 2 chiffres :

\(x_i\)	Probabilités
\(ln(1)\)
\(ln(1)\)
\(ln(3)\)

La somme des valeurs en sortie de la fonction Softmax donne 1.

Si une valeur d’entrée \(x_i\) diminue et que les autres restent identiques, alors sa probabilité augmente.

Les probabilités associées aux valeurs [2,8,9] sont les mêmes que celles associées aux valeurs [4,16,18].

Des valeurs en entrée [1,1,1,1] donnent des probabilités équiprobables.

Si une valeur d’entrée \(x_i\) double, alors sa probabilité associée double aussi.

La fonction Softmax peut gérer des entrées avec des valeurs négatives.

Si toutes les valeurs d’entrée sont strictement négatives, alors l’évaluation de la fonction Softmax produit une erreur d’exécution.

Les probabilités associées aux valeurs [2,8,9] sont les mêmes que celles associées aux valeurs [12,18,19].

Si une valeur d’entrée reste constante et que toutes les autres valeurs diminuent, alors sa probabilité augmente.

Logit

Il s’agit d’un terme ayant un sens spécifique dans le domaine de l’apprentissage automatique. Le logit désigne les valeurs brutes (non normalisées) en sortie du réseau. Ainsi, dans les problèmes de classification, le logit est le vecteur de valeurs qui va ensuite être transmis à la fonction Softmax pour normalisation. Le logit est un vecteur de valeurs quelconques (non-normalisées) alors que le vecteur en sortie de la fonction Softmax est un vecteur de probabilités dont les valeurs sont dans l’intervalle [0,1] et dont la somme vaut 1.

Cross-Entropy Loss

On note r et e deux probabilités discrètes l’une correspondant à la référence terrain et l’autre à l’estimation du modèle. Ainsi on a :

\[\sum_i r_i = 1 \quad \text{et} \quad \sum_i e_i = 1\]

La Cross-Entropy Loss entre les distributions de probabilités r et e est définie par :

\[\mathrm{CrossEntropyLoss}(r, e) = - \sum_{i \,:\, r_i > 0} r_i \, \ln(e_i)\]

Cette formule n’est pas symétrique, la référence r est hors du log et la probabilité estimée e dans le log. On admet que l’entropie croisée est minimale lorsque les deux distributions sont identiques, c’est-à-dire lorsque \(r_i = e_i\) pour tout \(i\). Minimiser la Cross-Entropy Loss revient donc à faire tendre la distribution prédite e vers la distribution de référence r.

En classification

Dans le problème de classification, la distribution de référence \(r\) correspond à une distribution nulle partout sauf pour la catégorie \(k\) correspondant à la classe de référence pour laquelle nous avons \(r_k=1\).

L’expression de l’entropie croisée se réécrit donc dans ce contexte :

\[CrossEntropyLoss(r,e) = - \ln{\left(e_k\right)}\]

Sous Pytorch

Avertissement

Dans PyTorch, la fonction CrossEntropyLoss prend en entrée des logits et non des probabilités.

Cependant, lors de l’appel de la fonction CrossEntropyLoss de PyTorch, on applique d’abord la fonction Softmax aux logits puis ensuite la CrossEntropyLoss. Pourquoi cela ? La fonction Softmax est basée sur des fonctions exponentielles. Or ces dernières générent des overflow pour des valeurs de logits >89 ou aussi des underflow pour les logits les plus faibles. En combinant le calcul du Softmax et de la Crossentropy dans une même fonction, PyTorch peut combiner et transformer ces deux formules afin de réduire cette instabilité numérique. Cette amélioration ne serait pas possible si l’on découpait ce calcul en deux étapes.

En résumé, la fonction CrossEntropyLoss accepte en entrée :

les logits

la valeur k indiquant la catégorie de référence

Exemples

import torch
import torch.nn as nn

logits = torch.tensor([[2.0, 1.0, 0.1]])
target = torch.tensor([0])

loss_fn = nn.CrossEntropyLoss()
loss = loss_fn(logits, target)

>> tensor(0.4170)

Ce qui par vérification donne :

import math
p = math.exp(2) / (math.exp(1) + math.exp(1) + math.exp(0.1))
-math.log(p)

>> 0.417030

Probabilité (%)	100	90	50	20	10	5	1
Cross-Entropy Loss	0.000	0.105	0.693	2.303	1.609	2.996	4.605

Efficacité

Prenons un exemple où la vraie classe est chat :

le modèle prédit chat avec 90% → loss faible de 0.1

le modèle prédit chat avec 50% → loss faible de 0.7

le modèle prédit chat avec 10% → loss élevée de 2.303

le modèle prédit chat avec 1% → loss très élevée de 4.605

La Cross-entropy Loss augmente lentement lorsque l’on s’éloigne des 100%, mais très rapidement lorsque l’on s’éloigne des 10% :

Passer de 100% → 90% : +0.105

Passer de 20% → 10% : +0.693

Que cela sous-entend-il ? Examinons le gradient par rapport aux logits :

\[\frac{\partial L}{\partial z_k} = e_k - r_k\]

où :

\(L\) est la Cross-Entropy Loss
\(z_k\) est le logit associé à la classe \(k\)
\(e_k\) est la probabilité prédite pour la classe \(k\), obtenue après application de la fonction softmax
\(r_k\) est la probabilité de référence pour la classe \(k\) (égale à 1 si \(k\) est la classe correcte, 0 sinon dans le cas one-hot)

Ce résultat montre que le gradient correspond simplement à la différence entre la probabilité prédite et la probabilité de référence. Ainsi, lorsque la probabilité prédite \(e_k\) est faible, le gradient pour le logit k reste proche de 1 ce qui reste elevé. Ainsi, même pour des probabilités faibles, la Cross-Entropy Loss permet une correction rapide de la probabilité estimée sur la classe de référence. Cela garantit un apprentissage beaucoup plus rapide et efficace.

Mauvaise gestion du bruit

La Cross-entropy Loss pénalise fortement une probabilité faible sur la classe de référence. Ainsi, face à un label de référence incorrect ou face à un outlier, la Cross-entropy Loss va avoir tendance à surapprendre ce cas particulier pour diminuer la Loss globale. Cet « contorsion » maladroite va pénaliser les capacités d’apprentissage du modèle. La Cross-entropy Loss est donc très sensible au bruit.

Polarisation

La Cross-Entropy Loss encourage le modèle à produire des probabilités très proches de 0 ou de 1. Cela peut conduire à des prédictions excessivement polarisées, même dans des situations ambiguës où plusieurs classes sont plausibles (en effet, sur certaines images d’un dataset, la différence entre deux catégories n’est pas toujours évidente). En utilisant la Cross-Entropy Loss, le modèle ne peut hésiter même lorsqu’il le devrait.

Remarque

La Cross-Entropy Loss n’est pas directement liée à la précision (accuracy) du modèle. En effet, il est possible qu’un modèle obtienne 90% de prédictions correctes tout en ayant une Cross-Entropy Loss élevée, tandis qu’un autre modèle peut avoir une Loss plus faible mais seulement 80 % de bonnes prédictions.

Pourquoi ? La Cross-Entropy Loss dépend de la probabilité attribuée à la classe correcte. Plus cette probabilité est élevée, plus la Loss est faible. À l’inverse, si la probabilité attribuée à la classe correcte est faible, la Loss sera élevée, même si la prédiction reste correcte.

La précision (accuracy) dépend uniquement du fait que la probabilité de la classe correcte soit la plus élevée parmi toutes les classes, sans tenir compte de sa valeur absolue. Ainsi, dans un problème à 100 classes, une probabilité de 2% pour la classe correcte peut suffire pour faire une prédiction correcte si toutes les autres classes ont une probabilité d’environ 1%. La prédiction est correcte et l’accuracy augmente. Cependant, du point de vue de la Cross-Entropy Loss, une probabilité de 2 % reste très faible, ce qui entraîne une Loss élevée.

La Cross Entropy Loss donne plus de poids aux erreurs importantes.

Dans PyTorch, la fonction de CrossEntropy Loss prend en entrée des probabilités.

Avec \(k=0\) et \(e_0=\frac{1}{e}\) et \(e_1=1-e_0\), alors l’entropie croisée vaut \(1\).

L’erreur associée à l’entropie croisée est nulle lorsque les probabilités sont équiprobables.

La Cross Entropy Loss produit des résultats polarisées en faisant tendre les probabilités vers 0% ou 100%.

Une Cross Entropy Loss élevée implique une mauvaise accuracy.

La Cross Entropy Loss est efficace car elle produit un gradient fort même lorsque les probabilités sont faibles.

La Cross Entropy Loss est nulle lorsque les probabilités de référence sont égales aux probabilités estimées.