1 - Repères et objets
Orientation des axes
Le repère de la scène 3D utilise une orientation non standard afin d’éviter la tentation de copier-coller du code depuis internet. Il vous est demandé explicitement d’utiliser ce repère car toutes les formules données dans la documentation vont utiliser ce repère particulier.
Consigne à respecter La convention pour le projet est de travailler avec les repères ci-dessous :
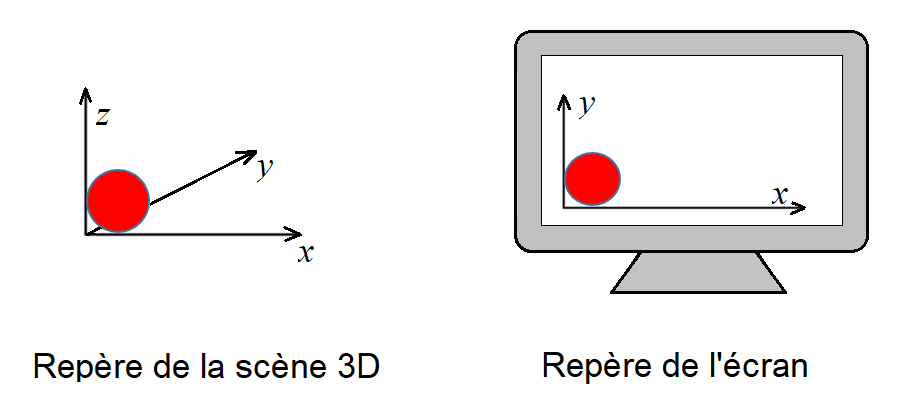
Quelques remarques sur les axes :
L’axe des abscisses de l’écran et de la scène sont tous les deux nommés x.
L’axe vertical y de l’écran correspond à l’axe z de la scène.
Les coordonnées de la scène 3D sont des nombres à virgule
Les coordonnées de l’écran sont des entiers.
Consigne à respecter Créez des variables différentes pour représenter les coordonnées dans le repère 3D et dans le repère écran.
La sphère
Modélisation
Consigne à respecter Pour modéliser nos sphères, nous utilisons les coordonnées sphériques présentées ci-dessous.
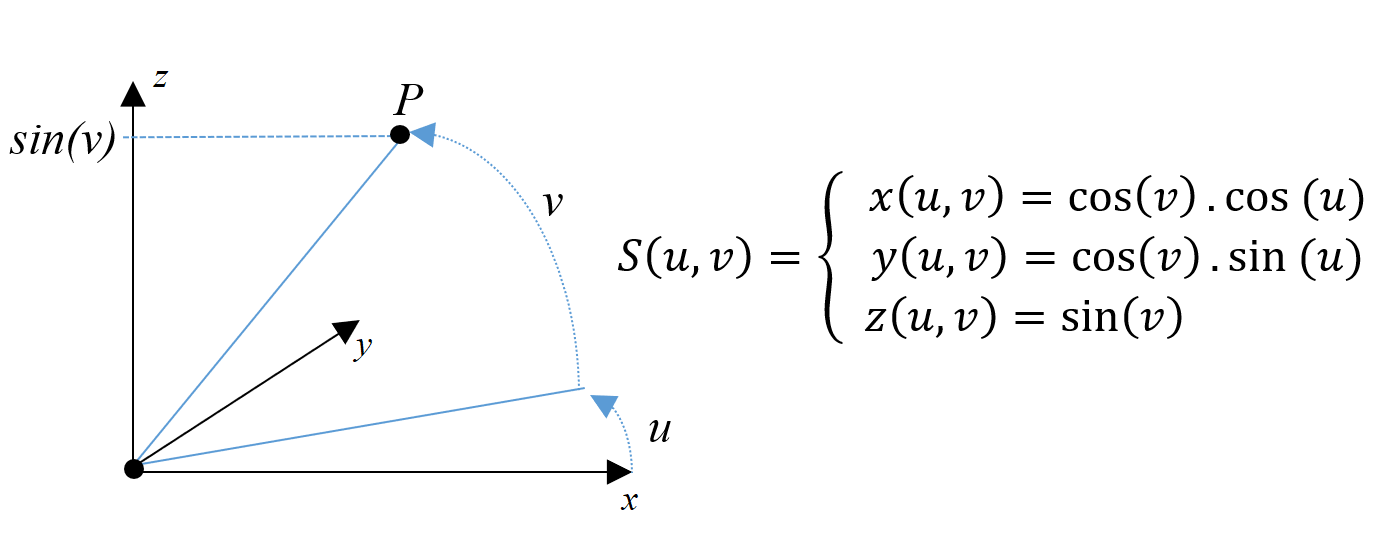
Pour positionner un point P sur une sphère de rayon 1, nous pouvons le faire à partir de deux angles u et v. Prenons une image en utilisant un canon d’artillerie. Pour positionner le tir, on fait d’abord tourner le canon sur son axe vertical pour qu’il pointe vers sa cible. L’angle u correspond à l’orientation du canon. Ensuite, les canonniers élèvent l’extrémité du canon pour régler la distance de tir. L’angle v correspond à cet angle d’élévation. Les deux rotations peuvent s’effectuer dans n’importe quel ordre, au final le canon sera placé de la même manière.
Espace de définition des paramètres
Rôle des paramètres :
Lorsque u varie dans l’intervalle \([0,2\pi]\), le point courant décrit un cercle horizontal. Il effectue un tour complet autours de l’axe vertical. On peut considérer que ce paramètre règle la longitude du point courant.
Lorsque v varie dans l’intervalle \([\frac{\pi}{2},\text{-}\frac{\pi}{2}]\), le point courant décrit un demi-cercle dans un plan vertical, allant d’un pôle à un autre. On peut considérer que ce paramètre règle la latitude du point courant.
Consigne à respecter Les paramètres de la sphère évoluent dans : \((u,v)\in [0,2\pi]\times[\pi/2,\text{-}\pi/2]\)
Sphère quelconque
Pour décrire une sphère dans une scène, il faut ajouter des paramètres supplémentaires : le rayon \(R\) et les coordonnées du centre C. Ainsi, nous obtenons pour une sphère \(M(u,v)\) la formulation suivante :
Normale en un point
Connaître la normale en un point de la surface d’un objet permet de calculer les effets d’illumination. Pour la sphère, il est inutile de se lancer dans des calculs complexes. Il suffit de remarquer que la normale correspond au rayon joignant le centre de la sphère et le point courant.
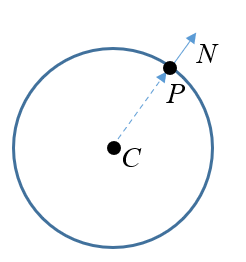
Ainsi nous avons : \(Normale(u,v)=S(u,v)\)
Remarque : l’expression de la normale est indépendante de la valeur du rayon.
Exercice
Placez les points suivants sur la surface de la sphère unitaire
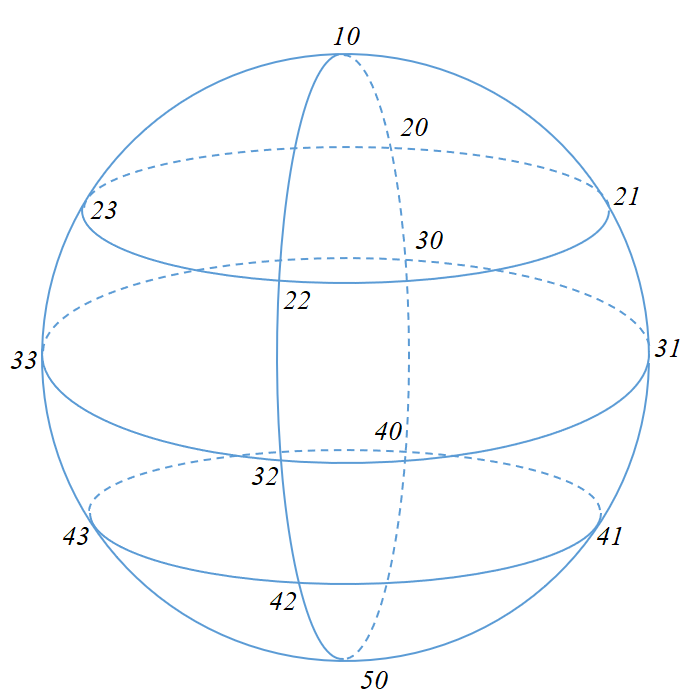
Pour chaque couple u,v, donnez la position correspondante sur le schéma :
Expression |
Type |
Valeur |
|
|---|---|---|---|
\((0,0)\) |
\((\pi,0)\) |
||
\((\frac{3\pi}{2},0)\) |
\((\frac{\pi}{2},0)\) |
||
\((0,\frac{\pi}{2})\) |
\((\pi,\frac{\pi}{2})\) |
||
\((0,\text{-}\frac{\pi}{2})\) |
\((0,\text{-}\frac{\pi}{4})\) |
||
\((\pi,\frac{\pi}{4})\) |
\((\frac{\pi}{2},\text{-}\frac{\pi}{4})\) |
Dans le code du projet
Pour afficher une sphère, dans le code fourni ci-dessous, nous avons échantillonné plusieurs points à la surface d’une sphère unitaire. Pour cela, nous incrémentons les valeurs de u et de v dans une double boucle, ceci en utilisant un pas constant. Une fois un point obtenu à la surface d’une sphère unitaire, nous multiplions ses coordonnées par le rayon de la sphère et nous ajoutons les coordonnées du centre. Nous obtenons ainsi un point 3D dans une scène 3D.
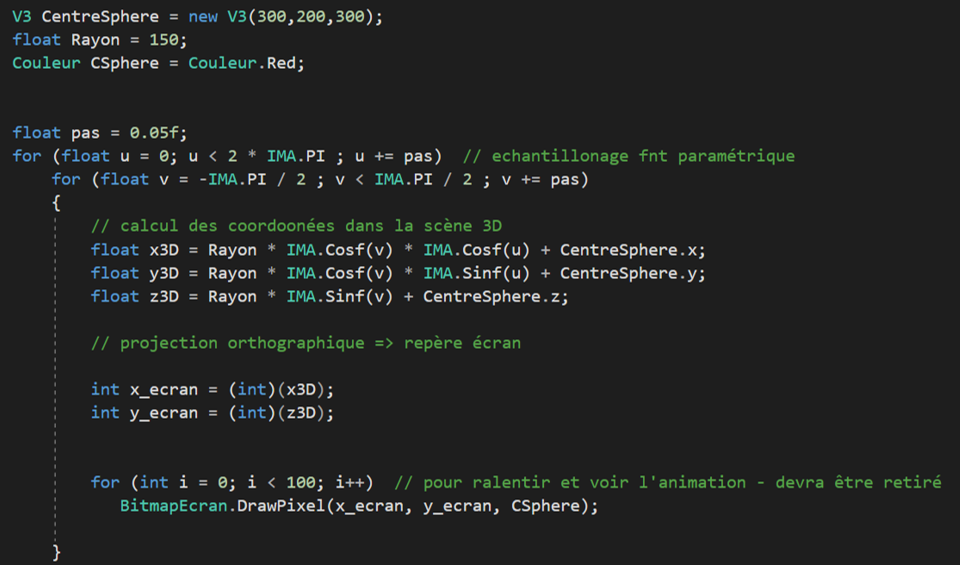
Dans un deuxième temps, nous cherchons à afficher le point 3D dans le repère de l’écran. Pour cela, nous effectuons une projection orthographique :
\(x_{ecran} = (int) x_{3D}\)
\(y_{ecran} = (int) z_{3D}\)
La projection orthographique ne gère pas la perspective (rétrécissement des objets lorsqu’ils s’éloignent de la caméra). Une fois les coordonnées écran calculées, nous affichons le point en tenant compte de la couleur de la sphère.
Travail à effectuer Retirez la ligne for(int i = 0 ; i < 100 ; i++) pour accélérer l’affichage. Modifiez la valeur du pas d’échantillonnage afin d’augmenter le nombre de points présents sur la sphère. Trouvez une valeur adéquate afin que la sphère apparaisse pleine à l’écran (sans trou) comme dans l’exemple ci-dessous :
Le parallélogramme en 3D
Modélisation
Le parallélogramme dans la scène 3D se positionne de manière quelconque, il n’est pas forcément horizontal ou vertical. Comme pour la sphère, nous allons le modéliser en utilisant une surface paramétrique :
Avec :
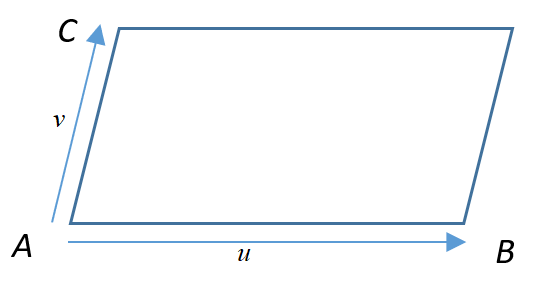
Exercice
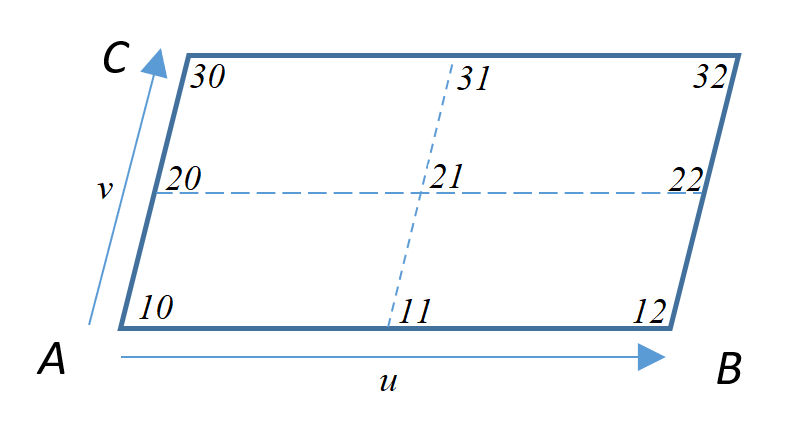
Pour chaque couple u,v, donnez la position correspondante sur le schéma :
Expression |
Type |
Valeur |
|
|---|---|---|---|
(0,0) |
(0,1) |
||
(1,0) |
(1,1) |
||
(0,½) |
(½,0) |
||
(½,½) |
Dans le code du projet
Pour afficher un rectangle plongé dans notre scène 3D, nous avons échantillonné plusieurs points à sa surface. Pour cela, nous choisissons une origine à ce rectangle (le point A), ainsi que deux vecteurs correspondant aux deux côtés émergeant de A. En incrémentant les valeurs de u et de v dans une double boucle, ceci en utilisant un pas constant, nous arrivons à calculer la position de plusieurs points 3D présents à la surface de ce rectangle. Les plages de valeur des paramètres u et v sont comprises entre 0 et 1.
Travail à effectuer Retirez la ligne for(int i = 0 ; i < 100 ; i++) pour accélérer l’affichage. Modifiez la valeur du pas d’échantillonnage afin d’augmenter le nombre de points présents sur le rectangle afin qu’il apparaisse plein (sans trou) comme dans l’exemple ci-dessous :

Le triangle en 3D
Modélisation
Le cas du triangle correspond à un cas particulier du parallélogramme, car il correspond à la moitié de la surface du parallélogramme :
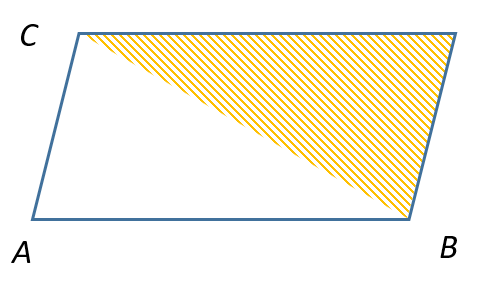
Exercice
Travail à effectuer Dans le code du projet, ajoutez une contrainte entre les paramètres u et v (une condition) afin que l’affichage produit corresponde au triangle ci-dessous :
