3 - Textures
Historique
Quels facteurs ont joué dans l’amélioration du rendu des jeux vidéo ?

On constate une montée en gamme. Pourtant, on compare ici des surfaces de bâtiments, c’est-à-dire des géométries relativement pauvres car assez plates. La différence de qualité se fait principalement dans l’augmentation de la densité des textures. A gauche, sont utilisées des textures 256x256 (une texture par habit, mur, visage, sol, drapeau, ciel…). Comptez environ 80 textures RGB pour cette scène, cela fait un total de 256x256x80x3 = 16Mo soit le maximum pour la mémoire GPU de l’époque. En 2004, on passe au Giga de mémoire sur les cartes graphiques, ce qui permet d’embarquer des textures 1024x1024 ou plus. A cette époque où la résolution d’écran standard était 1024x768, nous avions donc une texture aussi fine que la matrice du moniteur. Ainsi, regarder un mur de face, revenez à regarder une photo de ce mur, résultat photoréaliste garanti !
Coordonnées uv
Texture
Une texture correspond à une image 2D qui va servir à peindre un objet. Afin de rendre indépendante la texture de la résolution de son image d’origine, nous utilisons des coordonnées uv normalisées dans l’espace [0,1]x[0,1]. Ces coordonnées permettent de se repérer sur la surface de la texture. Ainsi la coordonnée uv=(0,0) correspond à la couleur présente en bas à gauche sur l’image d’origine :
Projections
Il y a plusieurs moyens de « peindre » un objet à partir d’une texture. Un des plus classiques est la projection. Vous pouvez voir plusieurs exemples ci-dessous où une texture de damier est projetée en mode planaire, cylindrique et sphérique sur une sphère :
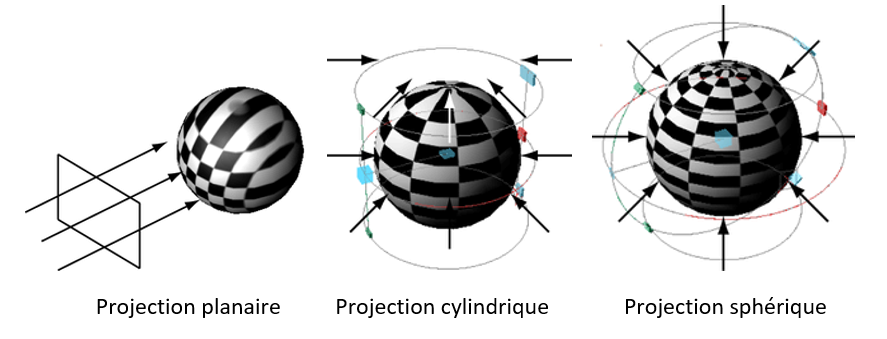
Ces techniques nécessitent des opérations complexes pour calculer la projection inverse permettant d’identifier la coordonnée uv associée à chaque point de la surface de l’objet. Nous allons présentée une autre approche moins gourmande en calculs et couramment utilisée sur les GPU. Cette approche est parfois déroutante pour certains élèves car elle n’a pas d’interprétation physique ou mathématique. Elle est juste simple à mettre en place.
Correspondance uv
Dans notre projet, les objets géométrique sont des surfaces paramétriques utilisant 2 paramètres (s,t). Ces deux valeurs permettent d’obtenir les coordonnées d’un point à la surface de l’objet. Les paramètres (s,t) évoluent sur un domaine propre à chaque surface. Nous allons appliquer une transformation linéaire pour amener chacun des ces paramètres dans l’intervalle [0,1]. Ces deux nouvelles valeurs normalisées vont définir nos deux valeurs (u,v). Nous les utilisons pour lire une couleur sur la texture. Pour terminer, nous associons au point 3D calculé la couleur trouvée. Voici un schéma qui résume ce traitement :
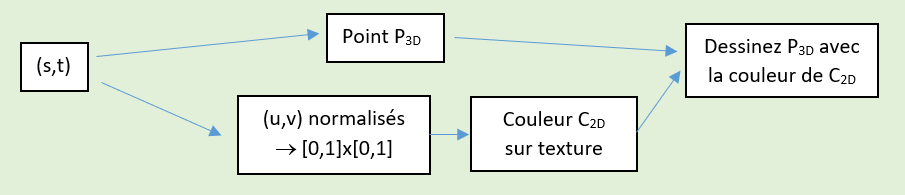
Voici par exemple ce que cela donne dans le cas de la sphère :
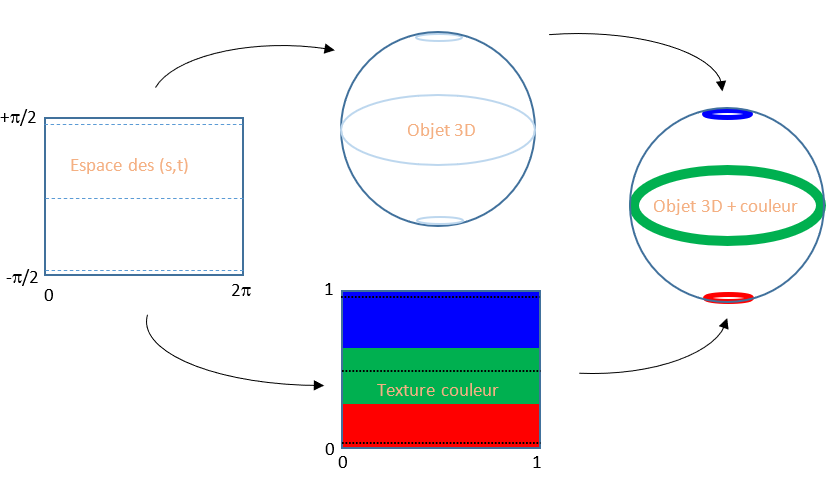
Cette projection pourra sembler familière à certains car elle correspond à la projection de Mercator, la projection utilisée sur les planisphères. Elle en subit d’ailleurs les mêmes défauts. Par exemple, le Groenland apparaît comme une île immense alors sur le planisphère alors que dans la réalité, sa surface est bien plus faible. En utilisant cette projection, la portion de texture utilisée au niveau des pôles est écrasée pour finalement couvrir une faible surface, c’est l’effet Knacki Ball, où la peau qui recouvre ces mini-saucisses finit écrasée aux extrémités. Voici un rendu utilisant une texture quadrillée afin de montrer l’effet de pincement de la texture aux pôles :

La classe Texture
Dans le projet, la classe Texture permet de gérer le chargement et l’utilisation d’un fichier image comme texture. On trouve :
Un constructeur prenant en paramètre un chemin de fichier. L’image est automatiquement chargée en mémoire par la librairie dot net qui sait lire plusieurs formats d’image comme bmp, png ou jpg.
Une fonction qui à partir des coordonnées uv retourne un objet Couleur avec des valeurs RVB normalisées. Cette fonction accepte des valeurs uv en dehors de l’intervalle [0,1] en ne tenant compte que de la partie fractionnaire des valeurs uv. Pour calculer la couleur à partir d’une coordonnée uv, cette fonction effectue une interpolation linéaire des couleurs à partir des 4 pixels avoisinants.
Travail à effectuer Identifiez parmi les fichiers du projet celui contenant cette classe. Parcourez le fichier et identifiez les noms de chaque fonction.
Mise en place
Travail à effectuer A partir des fichiers joints au projet, appliquez des textures sur vos sphères. Injectez cette information couleur dans les modèles d’illumination précédemment mis en place.
Voici le résultat obtenu à partir des textures OR et METAL.

Consigne à respecter Attention la texture doit recouvrir une fois et une unique fois la totalité de l’objet, ni plus, ni moins. Vous disposez d’une texture uvtest.jpg vous permettant de déboguer votre application de texture. En utilisant cette texture damier de 8x8 sur une sphère, vous devez voir apparaître 8 cases sur la hauteur et seulement 4 cases sur la largeur car les autres cases servent à colorier l’arrière de la sphère.
Pour vous amuser, vous pouvez utiliser un générateur automatique de textures de test
Taille des textures
L’application d’une texture n’apporte pas toujours un rendu parfait, pourquoi ? La texture est une image avec une certaine résolution, l’objet affiché à l’écran a aussi une dimension en pixels (largeur/hauteur). Lorsque la taille de l’image d’origine est proche de celle de l’objet à l’écran, tout se passe correctement. Quand le ratio entre les tailles dépasse un facteur 2, des artefacts peuvent apparaître :
Cas 1 : Texture trop grande
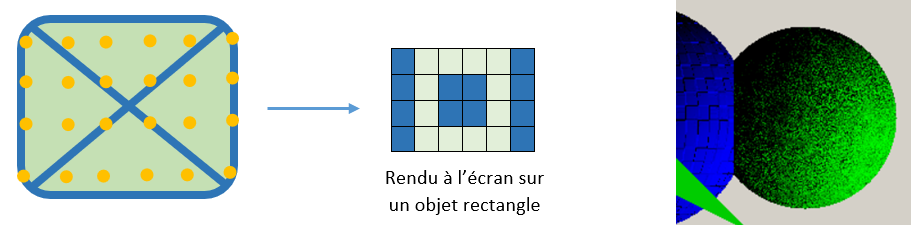
Par exemple, si vous appliquez une texture 512x512 sur un rectangle de 100 pixels de large à l’écran, seulement quelques pixels de l’image d’origine vont être utilisés pour construire l’image finale. Ce sous échantillonnage va amener différents problèmes, voir le schéma ci-dessus :
Dans l’exemple de gauche, les diagonales présentes dans la texture disparaissent du rendu final.
Dans l’exemple de droite, une texture détaillée génère un rendu final bruité.
Cas 2 : Texture trop petite
Dans ce cas, les pixels de l’image d’origine vont être étirés pour faire apparaître des gros carrés à l’écran.
Solution
Si une texture est trop grande par rapport à la taille de l’objet à l’écran, le rendu peut être amélioré en réduisant la résolution de l’image d’origine avec un logiciel adéquat comme Paint.exe ou le site photopea.com. Ces logiciels prennent en compte tous les pixels de l’image d’origine pour calculer l’image réduite ce qui permet d’avoir un résultat idéal. Lorsqu’une texture devient trop étirée et produit des gros carrés au rendu, il n’y a pas de solution miracle, il faudra alors rechercher une texture de taille supérieure.
Les moteurs 3D, pour éviter le problème de sous-échantillonnage, peuvent utiliser une stratégie appelée mip-mapping. L’idée est qu’une fois la texture chargée en mémoire GPU, on peut aussi calculer et stocker des réductions de cette texture avec un ratio de 1/2, 1/4, 1/8… Cette approche qui résout définitivement le problème nécessite cependant un doublement de la taille mémoire des textures, pour rappel 1+1/2+1/4+1/8… = 2.
En production
En production, les objets sont bien plus complexes que nos sphères. Ils sont décrits à partir d’un maillage composé d’une multitude de facettes triangulaires. Le principe que nous avons présenté ici s’applique aussi. Pour cela, chaque sommet du maillage est associé à des coordonnées (u,v) de la texture. Pour « peindre » une facette du maillage 3D, il suffit donc de transposer le triangle de couleurs issu de la texture vers la facette triangulaire 3D.