4 - Bump Mapping

Nous allons maintenant aborder un nouvel effet qui a permis d’effectuer une montée en gamme dans la qualité des images. Examinez les images ci-dessous :

Nous avons à gauche et à droite la même texture et la même géométrie. Pourtant, la qualité n’a rien à voir. Les pierres sur la droite ont l’air bien plus réelles !! Il s’agit ici d’un effet de Bump Mapping. Nous allons voir à quoi correspond cet effet et comment le mettre en place.

Principe du Bump-Mapping

Un cas simple

Examinons ce qu’il se passe sur une surface plane qui comporte une bosse et un creux. Comment notre cerveau fait-il pour interpréter cette scène ? Il va se servir de la direction ds rayons lumineux et de la position des ombres sur les surfaces pour savoir si elles correspondent à des bosses ou à des creux. Essayez de faire votre prédiction sur l’image ci-dessous !

Les normales

Pour mieux comprendre le rôle des normales dans le bump mapping, nous présentons un cas simple en 2D. Si le soleil est positionné en haut sur la gauche, en appliquant le modèle diffus, nous obtenons le rendu ci-dessous. Sur la zone 1 et 4, la normale est constante et orientée vers le haut. Le cosinus du diffus est donc constant sur cette partie et la luminosité est donc régulière. Sur la gauche de la bosse (milieu de la zone 2), la normale est colinéaire aux rayons du soleil. Ainsi, le cosinus du diffus vaut 1, la luminosité est alors maximale. En progressant vers la zone 3, l’angle entre la normale et le rayon du soleil passe de 0° à 90°. Ainsi, sur la droite de la zone 3, la luminosité est nulle. En quittant la zone 3 et en entrant dans la 4, une cassure se produit au niveau de la luminosité, en passant abruptement du noir au gris. Ainsi connaissant la direction des rayons lumineux, notre cerveau interprète la transition : gris-clair-noir-gris comme la présence d’une bosse.

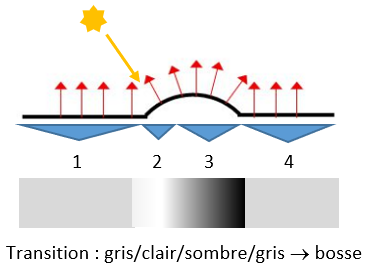
Un effet trompe-l’œil

Dans les exemples précédents, l’information lumineuse nous permet de déduire la géométrie fine de la surface : un léger trou, une légère bosse… Nous allons donc mettre en place un système de « trompe l’œil » qui ne modifie pas la géométrie d’origine des objets mais qui en faisant « bumper » les normales donne l’impression de la présence d’une texture de surface : striée, rayé, bosselée, rainurée, velours… On peut parler de texture de surface car les variations géométriques sont de faible hauteur par rapport à la taille de l’objet. On pourrait voir cela comme une peau que l’on colle à la surface de l’objet. C’est l’effet peau d’orange ou ballon de basket. La surface n’est pas lisse, on peut voir les variations, les sentir au toucher, mais au final, ces détails font moins d’1 mm d’épaisseur. Voici des exemples de textures de bump :

Cette technique appliquée à un rectangle conserve la géométrie plane, seules les normales bougent :

Les normales bumpées sont injectées dans les calculs d’illumination et produisent ainsi des effets d’ombrages et de reflets. Il est difficile de détecter ce trompe-l’œil. Prenons l’exemple de la sphère orange ci-dessous. Au centre, vous avez l’impression que cette surface est réellement bosselée. Pourtant il n’en est rien, il s’agit bien d’une sphère parfaite. Pour vérifier cela, il faut examiner le pourtour de la sphère. Vous constatez qu’il s’agit d’un cercle parfait.

Texture de bump

La bumpmap correspond à une texture en niveaux de gris dans laquelle nous stockons l’information sur la variation de hauteur de la surface. Ainsi, le noir va représenter une zone basse et le blanc une zone haute. La présence d’une tâche noire entourée de gris traduit la présence d’un trou :

Rappels mathématiques

Interprétation géométrique de la dérivée

La valeur de la dérivée \(f’(a)\) d’une fonction \(f\) nous donne la pente de la droite tangente au point \((a,f(a))\) de la courbe :

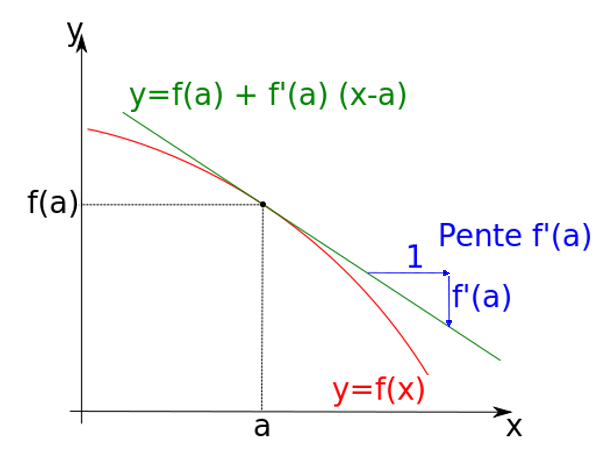
Produit vectoriel

Le produit vectoriel entre deux vecteurs permet de construire un nouveau vecteur perpendiculaire aux deux premiers. Voici la formule de calcul :

Dérivation partielle

La dérivée partielle de \(f(u,v)\) par rapport à \(u\) se calcule comme la dérivée de \(f(u)\) en considérant que \(v\) est une constante. Ainsi, lorsque \(f(u,v) = 2.u.v^3\), nous avons \(∂f(u,v)/∂u = 2v^3\) et \(∂f(u,v)/∂v = 6uv^2\).

La dérivée partielle d’une surface paramétrique M(u,v) s’exprime ainsi :

Interprétation géométrique de la dérivée partielle

En 3D, le vecteur des dérivées partielles \(∂S/∂u(u,v)\) correspond à la direction d’une droite tangente au point \(S(u,v)\). Cette direction s’obtient en faisant varier \(u\) de manière infinitésimale. La construction de \(∂S/∂v(u,v)\) est similaire.

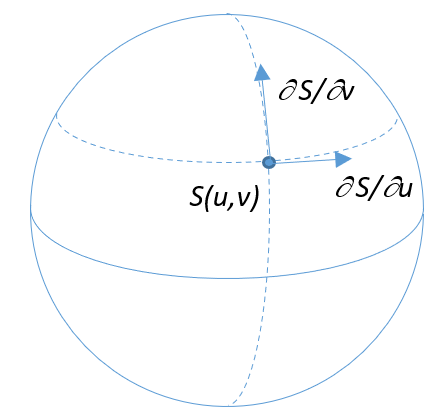
A partir des deux vecteurs issues des dérivées partielles, en appliquant un produit vectoriel il est possible d’obtenir le vecteur normal de n’importe quelle surface paramétrique. Il reste une ambiguïté sur sa direction qui peut être orientée vers l’intérieur ou l’extérieur. Ainsi, nous pouvons définir le vecteur normal \(N(u,v)\) normalisé ainsi :

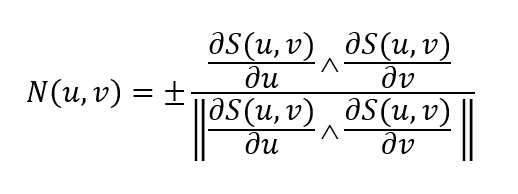
Mise en place

Calculs préliminaires

La texture de bump nous fournit une information de variation de hauteur : \(h(u,v)\). Le point \(M’(u,v)\) subit une élévation ou un abaissement par rapport à la surface d’origine. Ainsi, les coordonnées du point \(M’(u,v)\) s’obtiennent en prenant le point \(M(u,v)\) et en le déplaçant dans la direction de sa normale \(N(u,v)\) d’une distance \(h(u,v)\):

\[M'(u,v) = M(u,v) + h(u,v) \times N(u,v)\]

Nous cherchons maintenant à déterminer \(N’(u,v)\) la normale de la surface « bumpée ». C’est cette information qui nous intéresse car à aucun moment nous utiliserons le point \(M’\) dans notre programme. Par application des règles de calcul de dérivation, nous obtenons :

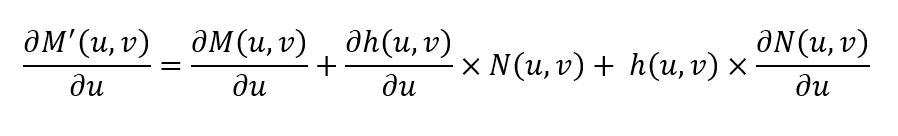
Attention, à ce niveau, la grandeur \(∂h/∂u\) est un réel qui est multipliée à un vecteur. Par contre, \(∂N/∂u\) est un vecteur multiplié à un réel, ce qui donne aussi un vecteur, donc, tout va bien. Le chercheur inventeur du BumpMap (Blinn, J., “Simulation of Wrinkled Surfaces”, Proceedings SIGGRAPH 1978) appliqua une approximation très intéressante. En effet, il remarqua que le Bump correspondant à des effets d’hauteur très faibles par rapport à la taille des objets. Ainsi, le 3ème terme dans l’équation ci-dessus peut être ignoré car le paramètre \(h(u,v)\) est une quantité très faible par rapport aux autres vecteurs. Ainsi nous avons :

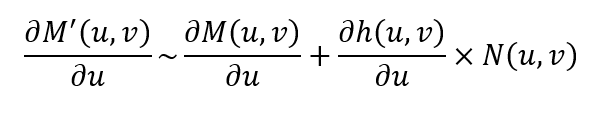
Travail à effectuer

Calculez \(∂M'/∂v\) et effectuez un produit vectoriel entre \(∂M'/∂u\) et \(∂M'/∂v\) pour obtenir la partie droite de l’équation ci-dessous. Identifiez les termes T2 et T3 correspondant.

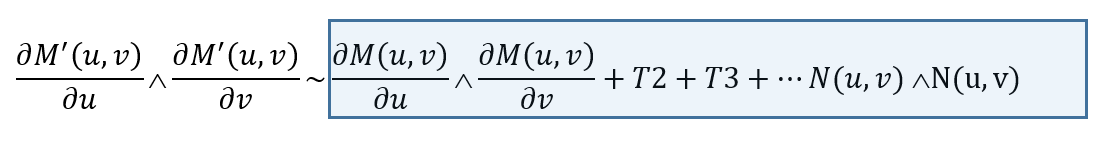
Le 4ème terme est égal au produit vectoriel de deux vecteurs colinéaires, il est donc nul et peut être supprimé. Le premier terme, si vous l’examinez, doit vous rappeler la définition du vecteur normal de la surface d’origine. Il faut maintenant intégrer le facteur \(K\) permettant de régler l’intensité de l’effet de Bump. Ainsi, en modifiant notre expression, nous obtenons la formule finale :

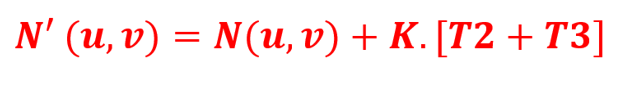
La classe Texture

Dans le projet, la classe Texture permet de gérer la texture de Bump. Elle fournit une fonction permettant d’évaluer les grandeurs \(∂h/∂u\) et \(∂h/∂v\).

Travail à effectuer Identifiez le nom de la fonction qui cacule les valeurs \(∂h/∂u\) et \(∂h/∂v\).

Implémentation

Pour rappel :

Les grandeurs \(∂h/∂u\) et \(∂h/∂v\) sont calculées depuis un objet texture.

Les grandeurs \(∂M/∂u\) et \(∂M/∂v\) sont à calculer à la main et à intégrer dans le programme.

Le facteur \(K\) est à déterminer pour que l’effet soit saisissant !

Voici le résultat que vous devez obtenir avec les textures et les bumpmaps fournis dans le projet :

Travail à effectuer Implémentez le bump mapping sur les sphères.

Attention, l’opérateur ^ est moins prioritaire que les autres. Ainsi, l’expression A^B+D^C ne produira pas le résultat que vous attendez. Pensez à parenthéser correctement.