Effets graphiques

Mesh

Vous pouvez intégrer dans votre projet un lecteur d’objets 3D. Nous vous conseillons le format OBJ qui stockent l’information géométrique sous forme de triangles. Ce format inclut aussi les coordonnées uv de chaque sommet. Il est standardisé et très populaire. De plus il est relativement simple et bien documenté. Il est cependant difficile de trouver des objets accompagnés des fichiers de texture. Demandez de l’aide à l’intervenant si vous n’arrivez pas à en trouver.

Voici des liens intéressants :

• Le format OBJ

• Exemples

Soft shadows

Le processus d’occultation que vous avez mis en place produit des ombres dures (hard shadows) : leur contour est franc et leur intérieur est noir. Ces ombres sont réalistes un jour d’été car elles correspondent à des ombres issues d’une unique lampe directionnelle de forte intensité comme par le soleil. Mais ce n’est pas le cas des scènes d’intérieur.

Habituellement, depuis un point courant P à la surface d’un objet, on tire un rayon partant de ce point et allant vers la source lumineuse. Si une intersection se trouve entre la source et le point, il y a alors occultation et les rayons lumineux ne peuvent parvenir à ce point. Pour simuler des ombres plus réalistes, on va tirer cette fois plusieurs rayons, une dizaine par exemple, pour réaliser le test d’occultation. Cependant, chaque rayon va être déplacé aléatoirement de quelques degrés. Ainsi en moyennant les résultats obtenus, apparaîtra une ombre progressive avec des transitions plus douces. C’est l’algorithme dit des soft shadows.

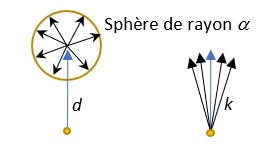
Comment déplacer un vecteur autours de sa position d’origine ? Notons \(d\) le vecteur direction actuel (normalisé). Générons aléatoirement une direction unitaire \(r\) (voir fin du chapitre amélioration du moteur 3D). Pour déplacer le vecteur \(d\), nous allons calculer un nouveau vecteur \(k\) ainsi :

\[k = d + \alpha . r\]

Il suffit après ce calcul de normaliser le vecteur \(k\).

Plus la valeur de \(\alpha\) est proche de 0, moins les variations sont importantes. Une valeur de 0.2 par exemple peut être un bon point de départ. Lorsque \(k\) vaut 0, on retrouve les hard shadows du départ, et plus on augmente \(k\), plus les transitions vont s’étaler. Du bruit pourra apparaître car nous faisons un échantillonnage aléatoire. Pour remédier à cela, il faudra augmenter le nombre de vecteurs utilisés pour effectuer la moyenne.

Tore

Dans le plan, un cercle de rayon \(a\) centré au point \((0,b)\) a comme paramétrisation :

\[\begin{split}\begin{equation} T(u) = \left\{ \begin{array}{lr} a.\cos(u) + b\\ a.\sin(u) \end{array} \right. \end{equation}\end{split}\]

La surface paramétrique du Donut correspond à la rotation de ce cercle autours de l’axe vertical :

\[\begin{split}\begin{equation} T(u,v) = \left\{ \begin{array}{lr} (a.\cos(u) + b).cos(v)\\ (a.\cos(u) + b).sin(v)\\ a.\sin(u) \end{array} \right. \end{equation}\end{split}\]

L’étape d’inversion des coordonnées 3D vers les coordonnées uv sera difficile à résoudre. Le plus simple consiste à échantillonner cette surface en créant une collection de rectangles. Il suffit alors d’intégrer ces éléments dans votre scène. Les coordonnées uv peuvent servir à texturer cette surface avec l’UV mapping habituel.

Vous pouvez étendre cette méthode aux surfaces de révolution en faisant tourner un profil autours d’un axe vertical. Voici un exemple ci-dessous :

Un beau vase dans le projet ! Si vous examinez les détails, vous remarquerez les facettes sous forme de quad à la surface du vase.