7 - Raycasting
Algorithmique
Historique
Le premier jeu ayant réussi à mettre en place cette technique fut Wolfenstein 3D grâce au moteur développé par ID Software dans les années 1990. Ensuite, DOOM 1 utilisa aussi ce moteur 3D assez révolutionnaire pour l’époque. Ces deux jeux lancèrent l’ère des jeux de type FPS (First-person Shooter). Ils mettaient en scène des décors dans lesquels évoluaient divers ennemis. Il fallait donc gérer des problèmes d’occultation : le personnage est-il caché par le pilier ou est-il devant le pilier ? Le Raycasting apportait une solution performante pour les CPU de l’époque. L’algorithme disparut cependant avec l’arrivée des GPU mettant en place une solution plus simple avec l’algorithme du Z-buffer. Mais aujourd’hui, les jeux sont arrivés au maximum de ce que peut offrir la technologie du Z-Buffer. Cette approche va finir par être dépassée par les méthodes de lancer de rayons et d’illumination globale dont le Raycasting constitue le point de départ.
Principe
Le RayCasting signifie simplement « lancer un rayon » depuis la position de la caméra. Ainsi, le premier objet traversé par ce rayon correspond à l’objet qui doit être affiché à l’écran. Pour trouver cet objet, il faut tester l’intersection de ce rayon avec l’ensemble des objets de la scène et s’il y a plusieurs intersections conserver l’intersection la plus proche de la caméra :
Consigne à respecter Le raycast teste l’intersection d’un rayon avec chaque objet de la scène. Une méthode polymorphe peut être une bonne approche.
Perspective
La perspective peut se résumer à cette illustration de rails de chemin de fer :

Le RayCasting apporte la perspective à notre image :
Si on recule un objet dans la scène alors sa taille va diminuer à l’écran.
Si deux lignes sont parallèles dans la scène, alors elles apparaissent comme deux lignes orientées vers un même point de fuite sur l’image finale.
Construire une image à l’écran
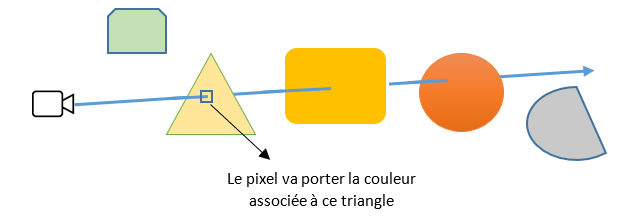
Pour dessiner les objets à l’écran, la méthode du Raycasting va lancer pour chaque pixel de l’écran un rayon qui part de la caméra et qui traverse ce pixel. Le résultat obtenu sert à colorer le pixel en question.
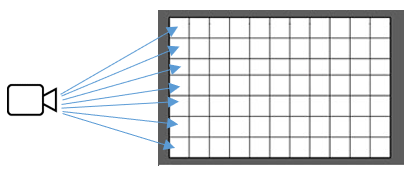
Pour notre projet, nous considérons que l’écran est une grille remplie de trous correspondant à chaque pixel. La caméra sera placée au milieu de l’écran en arrière, là où se trouve votre propre œil. Pour les unités de mesure, nous ne penserons pas en mètres ou en centimètres, mais en pixels. Ainsi, une longueur de 600 correspond à la longueur d’un segment de 600 pixels positionné à y3D = 0. Le fait de penser en pixels facilite énormément la création des objets de la scène. Par exemple, si votre écran a une résolution de 1200 pixels de large, en choisissant une sphère de diamètre 600 positionnée en y3D = 0, celle-ci devrait occuper la moitié de la largeur de l’écran. Dans ce système, positionner un objet en y3D = Largeur_Ecran équivaut à le placer derrière l’écran à une distance égale à la largeur de l’écran.
Généralement votre œil est éloigné de l’écran d’une distance égale à la largeur de l’écran. Ainsi, une position de la caméra qui correspond à votre réalité serait : (Largeur_Ecran / 2, -Largeur_Ecran, Hauteur_Ecran / 2). Pour cela, les méthodes GetWidth() et GetHeight() de la classe BitmapEcran vous seront utiles.
Boucles principales
La mise en place de l’algorithme réside dans une double boucle servant à parcourir l’ensemble des pixels de l’écran :
for (int x_ecran = 0 ; x_ecran ≤ largeur_ecran ; x_ecran++)
for (int y_ecran = 0 ; y_ecran ≤ hauteur_ecran ; y_ecran++)
{
P3 PosPixScene = new P3(x_ecran,0,y_ecran);
P3 DirRayon = PosPixScene – PosCamera;
Couleur C = RayCast(PosCamera, DirRayon, ListObjetsScene);
Affiche(x_ecran,y_ecran,C);
}
Angle de vision
Que se passe-t-il si l’on rapproche ou on éloigne la caméra dans la scène ? Le RayCast étant basé sur une méthode de lancer de rayon, l’angle de vision de la caméra va dépendre de sa position par rapport à l’écran, mais comment ?
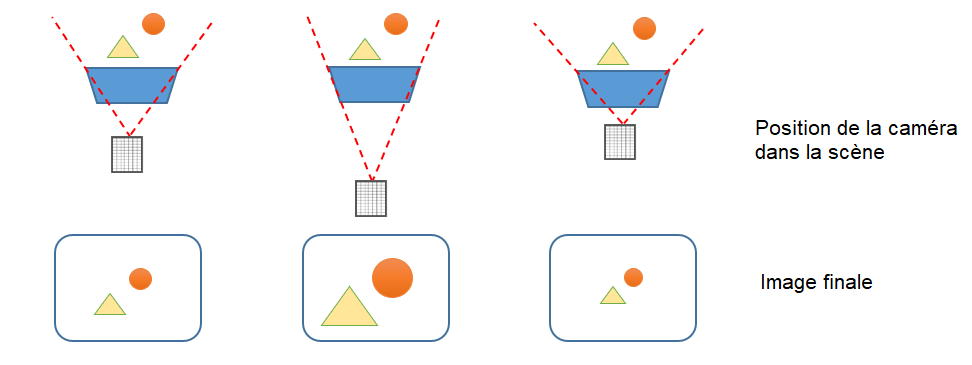
Pour imaginer le cône de vision de la caméra, il suffit de lancer 4 rayons partant de son objectif pour rejoindre les 4 coins de l’écran. Lorsque la caméra se rapproche de l’écran, son cône de vision s’ouvre et s’élargit. Si l’on recule, il se rétrécit. Lorsque vous regardez à travers une fenêtre, la logique est similaire. Si vous êtes proche de la vitre, vous voyez à 160° l’extérieur. Si vous reculez à l’intérieur de la pièce, vous voyez juste l’immeuble ou l’arbre en face de la fenêtre.
Quelle que soit la position de la caméra dans la scène, l’image créée à l’écran a une taille constante. Lorsque la caméra se rapproche de l’écran, l’angle de vision augmente (c’est un grand angle). Les objets précédemment à la frontière de la zone d’affichage sont maintenant à l’intérieur. La partie visible de la scène s’est élargie. En contrepartie, comme il y a beaucoup plus d’objets affichés, cela signifie que la taille des objets a rétréci dans l’image finale. A l’inverse, en reculant la caméra, les objets au centre s’agrandissent et les objets sur les bords quittent la zone d’affichage. Cela équivaut à augmenter la focale de votre appareil photo, c’est-à-dire zoomer. L’angle de vision rétrécit et les objets au centre s’agrandissent.
Gestion des intersections
Pour détecter si un rayon intersecte un objet il va falloir répondre à cette question pour chaque type de géométrie.
Intersection Rayon-Sphère
Afin de mener à bien la détection de l’intersection entre un rayon et une sphère, nous vous guidons dans cette démarche. Descriptions des éléments :
Le rayon : \(R(t)=R0+t.Rd\) avec \(t>0\), \(R_d\) et \(R_0\) connus
La sphère : de centre \(C(x,y,z)\) et de rayon \(r\)
Le rayon émis correspond à une demi-droite. Son origine \(R_0\) est située sur la caméra. Le paramètre \(t\) est positif car le rayon est orienté vers l’écran suivant une direction \(R_d\). Nous cherchons l’intersection entre ce rayon et la sphère. Cette intersection satisfait l’équation suivante :
En développant cette égalité, nous obtenons une équation du second degré de la forme : \(At^2+Bt+D=0\). Le déterminant \(\Delta=B^2-4AD\) nous indique s’il existe une intersection. Lorsque \(\Delta>0\), deux intersections sont possibles :
A ce niveau, il ne faut pas oublier la contrainte \(t>0\) car on ne s’intéresse qu’aux intersections présentes devant la caméra. S’il y en a plusieurs, on prendra la plus proche :
Si \(t1,t2 > 0\) : \(R(t_1)\) est l’intersection la plus proche
Si \(t_1<0, t_2>0\) : \(R(t_2)\) est la seule intersection devant la caméra
Si \(t1,t2<0\) : aucune intersection
Une fois le point d’intersection déterminé, il peut être utile de retrouver les paramètres uv associés à ce point car ils seront utiles plus tard dans ce projet. Pour cela, nous avons intégré dans le projet la fonction InvertCoordSpherique qui vous permettra d’effectuer cette opération. Attention, cette fonction utilise des coordonnées centrées (sur le centre de la sphère) !
Intersection Rayon-Parallélogramme
Afin d’éviter de lourds calculs, nous vous présentons une approche simple permettant de résoudre cette question. Nous allons d’abord résoudre l’intersection entre le rayon émis et le plan porté par les trois points \(ABC\) :
Le rayon : \(R(t)=R0+t.Rd\) avec \(t>0\), \(R_d\) et \(R_0\) connus
Le plan : \(A + uAB + vAC\) avec \(uv\) inconnus et \(ABC\) donnés
L’équation à résoudre est la suivante :
Nous calculons la normale au plan \(ABC\) :
En appliquant un produit scalaire sur l’équation précédente, on obtient :
Or AB et AC étant perpendiculaires à la normale n, nous avons finalement :
Ainsi, on déduit le point d’intersection \(I\) en calculant le résultat de l’expression : \(R_0 + t.R_d\) :
Il nous reste maintenant à retrouver les paramètres u et v. Nous savons :
L’utilisation du produit vectoriel nous permet d’écrire :
Ce qui se simplifie en :
Puis, par application du produit scalaire :
L’égalité du produit mixte : \((a \wedge b).c = (c\wedge a).b\) permet de transformer la formule en :
On obtient finalement une équation de la forme : \(u = K.AI\) avec \(K\) vecteur constant qui peut se précalculer dès que \(A, B, C\) (et donc \(n\)) sont connus.
En dernière étape, il nous reste à vérifier que le rayon traverse le parallélogramme. Il suffit pour cela de vérifier que \(0≤u≤1\) et que \(0≤v≤1\). Pour le cas de l’Intersection Rayon-Triangle, il s’agit d’un cas particulier où il suffit de rajouter comme contrainte supplémentaire sur \(u+v<1\) pour vérifier que l’intersection se trouve bien dans le triangle ABC.
Mise en place informatique
Liste des objets
Travail à effectuer Mettez en place une hiérarchie d’objets 3D contenant la classe sphère et la classe parallélogramme. Chacune d’entre elles doivent exposer des méthodes polymorphes permettant de gérer le Raycasting.
Rendu 3D
Travail à effectuer Créez une scène contenant des murs et quelques sphères. Chaque objet doit avoir sa propre couleur, ainsi le rendu de la scène doit correspondre a des zones de couleur uniformes associées à chaque objet.

La fonction DrawPixel() de la classe BitmapEcran permet de dessiner un pixel à l’écran.
Flux de traitement
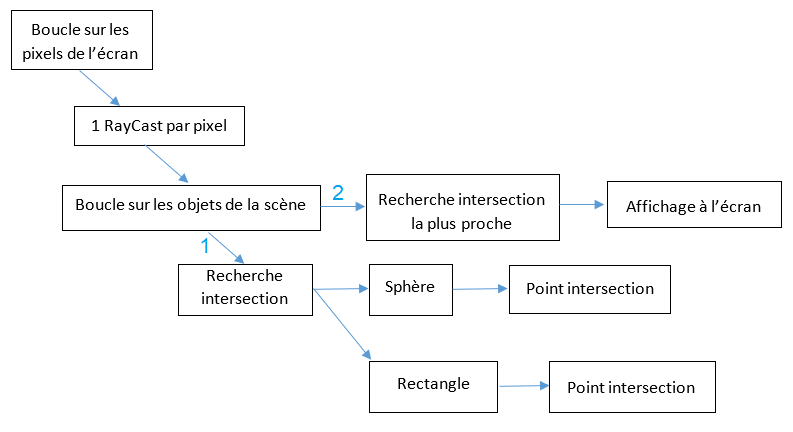
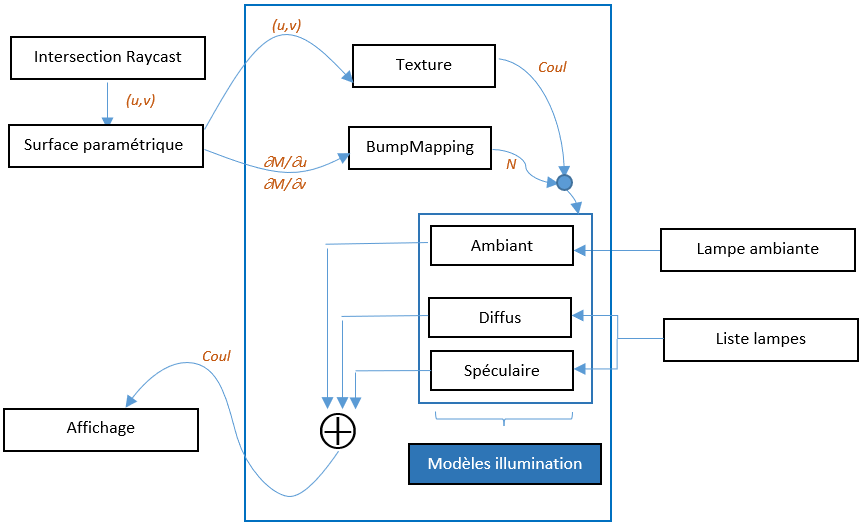
Après avoir intégré les textures et la gestion des illuminations, votre flux de traitement va se complexifier :