2 - Modèles d’illumination
Les modèles d’illumination décrivent comment la lumière se comporte à la surface d’un objet. La physique nous indique que les rayons peuvent être réfléchis, diffractés, absorbés… Nous allons voir dans ce chapitre comment modéliser ces comportements par des équations afin de simuler des rendus photo-réalistes.
Composantes RVB
Principe
Nous modélisons une couleur suivant un triplet de 3 valeurs correspondant aux intensités des couleurs R/V/B associées. La valeur 0 correspond à une absence de couleur et la valeur 1 à l’intensité maximale perceptible par l’œil. Ainsi la couleur (0,0,0) correspond au noir et la couleur (1,1,1) au blanc. Pour rappel, nous citons les 8 combinaisons de base :

Lors des calculs, il est possible de dépasser la grandeur 1 si par exemple beaucoup de lampes contribuent à l’éclairage d’une même zone. Ce n’est pas grave, car la classe Couleur stocke en fait des intensités lumineuses, valeurs physiques non bornées. C’est seulement au moment de l’affichage que ces intensités vont être écrêtées à la valeur 1. En effet, l’œil se comporte comme un capteur dont la sensibilité maximale est atteinte pour l’intensité 1, ainsi toute grandeur supérieure est automatiquement ramenée à cette valeur limite.
Addition et absorption
Addition
Cette situation se produit lorsque l’on superpose plusieurs lumières au même endroit. Dans cette approche, les différentes énergies lumineuses se cumulent. Par exemple, on peut produire cet effet en superposant la lumière émise par des spots comme dans le schéma ci-dessous :
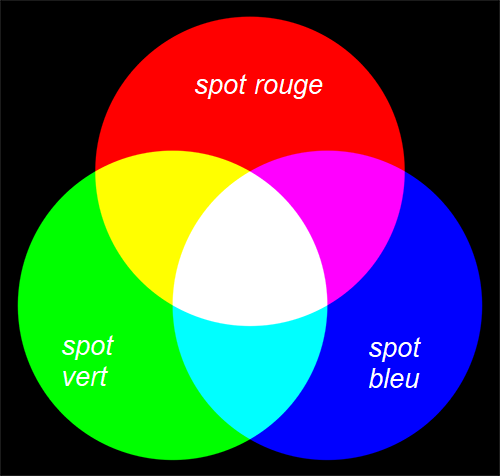
Pour modéliser une superposition de deux lumières, il suffit d’ajouter membre à membre les valeurs RVB de chaque lumière. Voici les résultats des différentes superpositions présentes sur le schéma :
La lumière rouge avec la lumière verte donne (1,0,0)+(0,1,0) soit (1,1,0) donc du jaune.
La lumière rouge avec la lumière bleue donne (1,0,0)+(0,0,1) soit (1,0,1) donc du magenta.
La lumière verte avec la lumière bleu donne (0,1,0)+(0,0,1) soit (0,1,1) donc du cyan.
Les trois lumières au centre : (1,0,0)+(0,1,0)+(0,0,1) soit (1,1,1) donc du blanc.
Absorption
Un objet cyan est perçue de cette couleur car il émet de la lumière cyan (0,1,1). Or, si cet objet est éclairée par une lumière blanche (1,1,1), cela sous-entend que la surface de cet objet renvoie du cyan car elle a absorbé la composante rouge (1,0,0) de la lumière blanche. Ainsi, un objet apparaît coloré car sa surface absorbe une partie des rayons lumineux reçus.
Pour modéliser l’absorption, nous utilisons une multiplication membre à membre des composantes RVB. Ainsi, la lumière blanche (1,1,1) éclairant un objet cyan (0,1,1) donne comme résultat : (1*0,1*1,1*1)=(0,1,1) soit du cyan. Il faut ainsi voir la couleur cyan de l’objet comme un filtre de couleur ! Comme la multiplication est une opération symétrique, nous remarquons que nous obtenons la même couleur finale si nous permutons le rôle des entrées : une boule blanche éclairée par une lumière cyan : (0*1,1*1,1*1)=(0,1,1). Par ce principe, on remarque qu’un objet sous une lumière noire (0,0,0) sera noir (0,0,0) ; résultat valide car cette configuration correspond à objet non éclairé.
Exercice
Trouvez la couleur perçue pour chacune des configurations suivantes :
Couleur de la lampe |
Couleur de l’objet |
Couleur perçue |
|---|---|---|
Blanc |
Blanc |
|
Cyan |
Bleu |
|
Cyan |
Jaune |
|
Rouge |
Magenta |
|
Bleu |
Vert |
|
Cyan |
Rouge |
Pour rappel :

Quizzz
L’impression jet d’encre utilise des encres : cyan magenta jaune et noir. Pourquoi ne pas utiliser seulement 3 couleurs ce qui est théoriquement suffisant ?
Cliquez ici pour voir la réponse
Une raison est la surcharge en encre du papier. En effet, on peut se passer de l’encre noire, mais pour fabriquer du noir, il faut alors superposer 3 couches d’encres ce qui rend le papier trop humide et il finit par gondoler. Pour éviter cela, on préfère utiliser de l’encre noire pour limiter la quantité d’encre déposée sur le papier.
Trajet des rayons lumineux
Dans les premiers modèles que nous allons développer, les rayons lumineux ont un comportement simplifié par rapport à la réalité. Quelle est la différence principale ?
Dans le monde réel, les rayons lumineux rebondissent sans cesse. Lorsqu’un rayon frappe un objet, la plupart du temps, il sera réémis dans une direction aléatoire. La couleur de ce rayon sera évidemment teintée par la couleur de cet objet. Les rayons réémis depuis cet objet vont alors aller éclairer d’autres objets et ainsi de suite. Comment s’achève la trajectoire d’un rayon lumineux ? Question difficile ! Cependant pour les rayons que nous percevons, leur trajectoire s’est terminée dans notre œil ! Pour obtenir une image photoréaliste, il faut donc pouvoir simuler des milliards de rebonds dans une scène, et cela nécessite une puissance de calcul importante.
Dans les années 2000, les jeux vidéo pouvaient seulement utiliser des modèles simulant un seul rebond. Dans cette configuration, le rayon lumineux part de la source et rebondit sur l’objet en direction de la caméra. Cela pourrait sembler suffisant surtout pour une scène extérieure où tous les éléments sont éclairés directement par le soleil, mais pour une scène d’intérieur c’est insuffisant. En effet, les rayons du soleil entrant par une fenêtre ne peuvent taper que sur le sol, ainsi le reste de la pièce reste non éclairé, ce qui n’est pas photoréaliste, cas (a) ci-dessous.
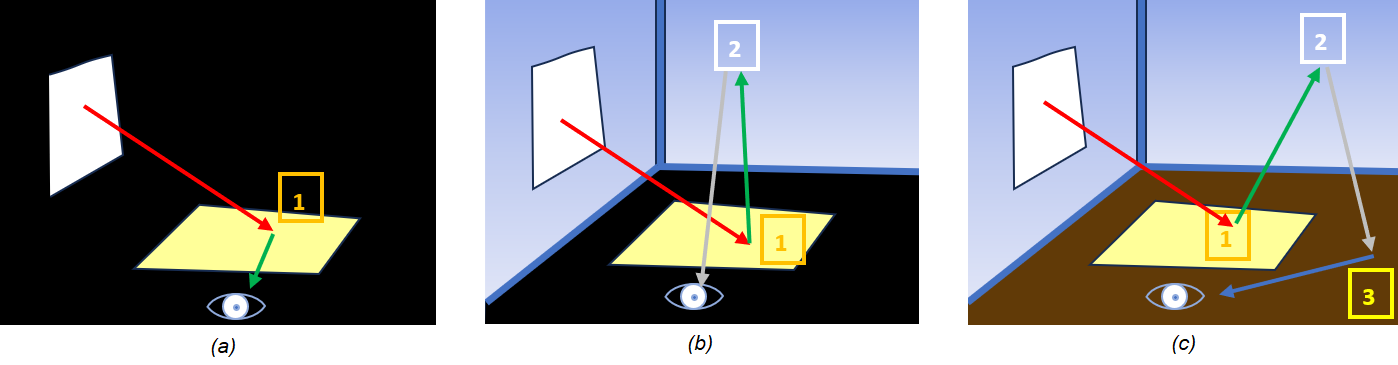
Interprétations des images :
Cas (a) - 1 rebond - Voici une scène d’intérieur éclairée par la lumière du jour. Le soleil produit des rayons lumineux parallèles et orientés vers le bas. Ceux-ci traversent la fenêtre pour éclairer une partie du sol et rebondir vers la caméra. Aucun rayon lumineux ne peut toucher les murs ou le plafond qui reste dans le noir complet.
Cas (b) - 2 rebonds - En autorisant un rebond supplémentaire, cette fois les rayons atteignant le sol peuvent aller éclairer les murs et le plafond avant de rebondir une deuxième fois vers la caméra. La zone lumineuse au centre se comporte ainsi comme une source indirecte (secondaire) qui vient éclairer certaine zone de la pièce non atteignable directement par les rayons traversant la fenêtre. Il reste cependant encore une partie dans le noir, il s’agit de la zone autours de la zone lumineuse sur le sol. Aucun rayon de niveau 2 ne peut l’atteindre.
Cas (c) - 3 rebonds - En permettant un 3ème rebond, nous obtenons une scène bien plus lumineuse. Si nous examinons le sol, il est cette fois éclairé dans sa globalité. Ici, le plafond et les murs ont joué leur rôle de source indirecte (tertiaire) en renvoyant des rayons provenant du centre du sol.
La classe Couleur
Dans le projet, vous trouverez une classe gérant la couleur. Cette classe dispose de :
Trois valeurs flottantes R,V,B
Constantes couleurs accessibles par la syntaxe : Couleur.Cyan
Deux constructeurs : Couleur(float R, float V, float B) et Couleur(Couleur c)
Des fonctions de conversion
De fonctions utilitaires
D’opérateurs surchargés
L’opérateur ✱ qui gère la multiplication des composantes RVB membre à membre
L’addition entre deux couleurs
La multiplication et division par un réel
Travail à effectuer Identifiez parmi les fichiers du projet celui contenant cette classe. Parcourez le fichier et identifiez le rôle et le nom de chaque fonction.
Modèle d’illumination ambiant
Principe
Il est très difficile de simuler le comportement de la lumière dans une scène. En effet, celle-ci rebondit sans-cesse d’un objet à l’autre produisant des éclairages indirects de toute sorte. Les premiers modèles que nous allons utiliser sont plutôt simples et ne simulent que des éclairages directs (1 rebond) depuis une source lumineuse. Ainsi, toutes les zones non directement éclairée restent noires dans le rendu final. Pour éviter cela, on triche, et on utilise le modèle d’illumination ambiant. Il s’agit d’une astuce informatique, le modèle ambiant ne correspond pas à une réalité issue des lois de la physique. Le modèle ambiant permet de relever la luminosité de toutes les zones non éclairées dans la scène, et ainsi il rehausse les zones sombres présentes dans l’image finale. C’est une sorte de lumière magique présente partout dans la scène et venant éclairer tous les objets sans se préoccuper des questions d’occultation. Cette lumière doit rester peu intense (de 5% à 15%) sinon le rendu de la scène sera surexposée.
La lampe ambiante
On peut choisir une lumière blanche pour jouer le rôle de lumière ambiante, mais on peut aussi choisir une couleur jaune si, par exemple, la scène correspond à grotte éclairée par une torche. On crée, informatiquement parlant, une lampe ambiante dont le seul intérêt est de définir la couleur de la lumière ambiante. Cette lampe est virtuelle : elle n’a pas d’existence dans la scène, pas de position, pas d’objet physique associé.
Formule
On utilise le modèle de l’absorption (multiplication membre à membre) car la couleur perçue à l’écran correspond à la couleur de la lumière ambiante teintée par la couleur de l’objet :
En étudiant cette formule, on peut remarquer qu’il est inutile de créer deux lampes ambiantes. En effet, on aurait \(C_{Amb1}×C_{Obj} + C_{Amb2}×C_{Obj}\) ce qui revient à écrire \((C_{Amb1}+C_{Amb2})×C_{Obj}\). Ainsi, deux lampes ambiantes peuvent se simplifier en une seule. La lampe ambiante est donc unique par convention.
Exercice
Calculez la couleur affichée à l’écran pour un objet de couleur [20% 50% 40%] éclairé par une lampe ambiante de couleur [80% 60% 40%].
Cliquez ici pour voir la réponse
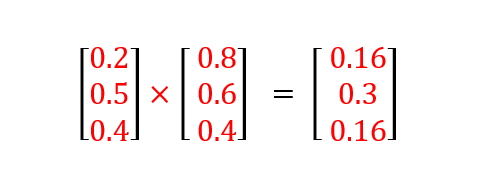
Test de l’ambiant
En utilisant le code actuel, mettez en place le modèle d’illumination ambiant sur la sphère. Choisissez une couleur pour la lampe ambiante et une autre pour la sphère. Vérifiez que la couleur affichée sur le rendu final correspond au résultat ci-dessous.
Cliquez ici pour voir les couleurs de référence

Les sources lumineuses
Les lampes en synthèse d’images sont des sources de lumière. Elles n’ont pas d’existence physique dans la scène ! Si vous voulez qu’une lampe existe physiquement, il faudra lui associer un objet 3D.
La lampe directionnelle

La lampe la plus courante est la lampe directionnelle, elle correspond à un éclairage extérieur provenant du soleil. Le soleil étant une source éloignée, ses rayons sont parallèles dans la scène. Ainsi les ombres produites par une même lampe directionnelle sont orientées dans la même direction. Par convention, une lampe directionnelle n’a pas de position dans la scène, elle est considérée comme étant placée à l’infini. Seul compte son orientation.
Nous vous demandons pour l’instant d’utiliser une unique lampe directionnelle blanche. En effet, son rendu est plus simple à valider et aussi à déboguer. Consigne à respecter
La lampe ponctuelle

Une lampe ponctuelle a une position dans la scène 3D. Ses rayons lumineux sont émis depuis cette source et partent dans toutes les directions. Les lampes ponctuelles produisent des éclairages plus complexes et sont plus difficiles à maîtriser. Elles sont souvent associées à une valeur de Decay (affaiblissement) car leur portée est relativement limitée. Elles permettent de modéliser des bougies, des lampes à incandescence, des spots… Les ombres s’orientent en fonction de la position de l’objet relativement à la source.
Présentation des modèles
Que peut signifier l’expression « modèle d’illumination » ? Un modèle d’illumination permet de modéliser les comportements de la lumière à la surface d’un objet. Tout d’abord, nous allons étudier un cas pratique avec une image de boules de billard.
Etude de cas

Sur cette photographie, nous avons une source principale correspondant à la lumière du soleil : les ombres ont même direction car tous les rayons lumineux sont parallèles. Sur la boule blanche, nous remarquons qu’une zone est plongée dans la pénombre. Elle correspond à la partie de la boule qui ne reçoit pas directement des rayons du soleil. Nous remarquons une courbe qui sépare la zone éclairée de la pénombre. Sur une sphère, cette séparation entre la zone claire et la zone sombre représente un cercle virtuel appelé terminateur. On remarque un dégradé dans l’intensité lumineuse allant du plus clair sur l’avant droit jusqu’à la zone de pénombre. Nous retrouvons l’existence de ce terminateur sur les autres boules de billard. Sur certaines boules, on remarque la présence d’un éclat de lumière en haut à droite.
Le modèle de Phong
Le modèle de Phong correspond à la superposition de trois modèles :
Le dégradé progressif qui se produit de la zone la plus claire jusqu’à la bordure du terminateur correspond au modèle diffus.
Sur l’ensemble des boules, un éclat est présent et semble orienté vers le soleil. Cet éclat correspond au modèle spéculaire. L’éclat se trouve parfois proche de la zone d’intensité maximale du diffus, mais leurs positions sont généralement différentes.
La zone dans la pénombre n’est pas noire, elle porte un niveau de luminosité faible simulé par le modèle ambiant.
Voici les différents effets produits par chaque modèle. Le résultat final sur la droite correspond à l’addition (superposition) des différentes contributions.

Le modèle de Phong n’est pas photoréaliste car par exemple, il ne gère par l’affaiblissement de la lumière en fonction de la distance à la source. Cependant, ce modèle a été construit pour représenter une scène avec une très bonne qualité et avec un faible coût en calcul.
Le modèle de réflexion diffuse
Présentation
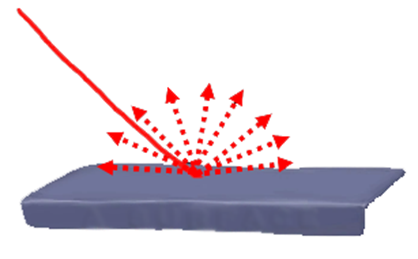
Il génère 90% de la luminosité d’une scène. C’est le modèle le plus commun et le plus classique. Dans ce modèle un rayon lumineux heurte une surface, se teinte suivant la couleur du point d’impact et réémet une multitude de rayons lumineux dans toutes les directions. Il faut noter qu’il n’y a pas de direction privilégiée. Ainsi en un point donné d’un objet, quelle que soit la position de la caméra autours de cet objet, la couleur produite par le modèle diffus ne change pas. Ainsi, lorsque l’on se promène dans une pièce, il y a une certaine stabilité des couleurs des différents objets, cela est dû au principe du modèle diffus.
Formule
En synthèse d’images, nous considérons uniquement les informations présentes à un point de la surface de l’objet. Nous ne tenons pas compte du reste de la surface. Toutes les formules données sont donc exprimées pour un point P donné dont la normale N est orientée vers l’extérieur (convention). Nous notons L le vecteur directeur des rayons lumineux. Par convention, le vecteur L est orienté dans le sens inverse du rayon lumineux : du point P vers la source :
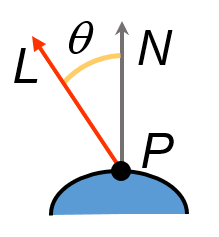
La Loi de Lambert nous donne la formule de calcul du modèle diffus : l’intensité de la lumière ne dépend que de l’angle \(\theta\) formé entre le vecteur lumière L et le vecteur normal à la surface N : \(I_{diff} = I_{source}.cos(\theta)\). Ainsi, en intégrant le modèle d’absorption des couleurs, nous obtenons comme formule :
Nous avons besoin de calculer la valeur de \(cos(\theta)\) sans connaître la valeur de l’angle \(\theta\). En effet, la fonction arccos doit être évitée à cause de son coût prohibitif. Pour cela, nous utilisons la formule du produit scalaire suivante : \(u.v=||u||.||v||.cos(\theta)\). Ainsi, avec deux vecteurs L et N normalisés, nous obtenons comme formulation du diffus :
Calcul du diffus : \((Coul_{Source}×Coul_{Obj}).prod_{scal}(N,L)\)
Il est parfois utile de rajouter un coefficient \(\rho_{diff}\) propre à un objet. Ce coefficient indique la capacité de cet objet à produire un effet de diffus. Ce coefficient multiplicatif compris entre 0 et 1 agit comme un potentiomètre et permet de régler l’intensité du diffus. En effet, pour un objet mât, le diffus est proche de 100% par contre pour un objet brillant ou métallique, le diffus est beaucoup plus faible.
Interprétation
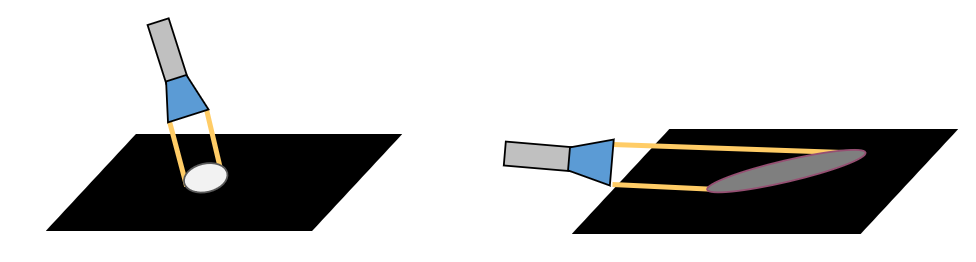
Pour comprendre la formule du modèle diffus, il suffit de se ramener à une expérience de physique basique. Si l’on prend une lampe de poche et qu’on la place perpendiculairement à une surface, cette lampe crée une zone circulaire éclairée vivement. Plus on penche la lampe, plus la zone de lumière s’agrandit et l’intensité lumineuse s’affaiblit, ce qui est normal puisque la même quantité de rayons lumineux éclaire une plus grande surface.
La classe vecteur 3D
Dans le projet fourni, la classe vecteur 3D permet de gérer toutes les opérations géométriques s’appliquant aux points et aux vecteurs. On trouve :
3 paramètres flottants x,y,z
Calcul de la norme d’un vecteur
Normalisation du vecteur courante
Divers constructeurs
Opérateurs de base + - et * par des flottants
Produit scalaire entre vecteurs : opérateur ^ ou fonction prod_scal()
Produit vectoriel entre vecteurs : opérateur * ou fonction prod_vect()
Travail à effectuer Identifiez parmi les fichiers du projet celui contenant cette classe. Parcourez le fichier et identifiez le rôle et le nom de chaque fonction.
Mise en place
La source lumineuse sera placée en haut à droite avec un éclairage de face. Ainsi, le vecteur lumière L sera égal à (1,-1,1)/√3.
Travail à effectuer Implémentez le modèle diffus sur la sphère.
Voici l’image de référence que vous devez obtenir :

Un piège se cache dans l’implémentation du diffus. Si vous implémentez la formule de base seulement, vous aurez un problème dans la zone de pénombre. Réfléchissez à ce qu’il se passe dans cette zone. Des rayons de lumière y parviennent ils ? Comment identifier cette configuration et comment la résoudre ?
Cliquez ici pour avoir la réponse à ce problème.
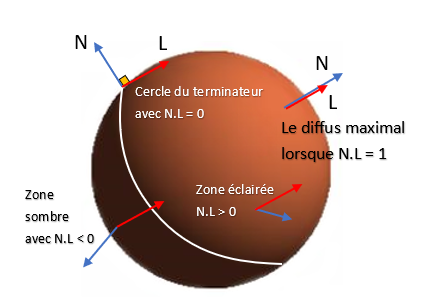
La zone dans la pénombre ne reçoit aucun rayon lumineux, elle correspond à la nuit sur terre. Le terminateur, frontière entre la pénombre et la zone éclairée, correspond aux points vérifiant N.L =0. Dans cette configuration, les rayons lumineux sont perpendiculaires à la normale de la surface ce qui sous-entend que les rayons lumineux sont rasants et que le soleil se couche. Sur la partie éclairée, N et L sont orientés dans la même direction, ce qui donne N.L>0. La zone portant la luminosité maximale correspond au point où N et L sont colinéaires. La pénombre se détecte quand les vecteurs N et L sont de direction opposée ce qui se produit lorsque N.L<0. Dans cette configuration, il ne faut pas multiplier le résultat du calcul N.L avec la couleur au risque de créer une couleur à valeurs négatives.
Le modèle de réflexion spéculaire
Etude de cas
Un ralentissement sur la route est une excellente occasion d’examiner des spéculaires. En effet, les peintures des carrosseries de voitures sont brillantes et sujettes aux reflets. La réflexion spéculaire correspond au comportement du miroir : le rayon lumineux frappe un objet et au lieu de rebondir dans une direction aléatoire comme dans le cas du diffus, le rayon rebondit dans une direction unique. Ainsi les éclats de lumière sur les carrosseries des voitures correspondent à des reflets de lumière provenant des sources environnantes : lampadaires, phares…

Le marché du luxe mise fortement sur la présence de spéculaires. En effet, la présence de reflets sublime les objets. Les bijoux misent principalement sur les reflets spéculaires, car il ne faut pas oublier qu’il s’agit de métal poli, idéal pour produire un effet miroir !

Les voitures et les bijoux ne sont pas les seuls objets susceptibles de produire des spéculaires. Toute surface brillante et polie de la vie courante peut créer cet effet . Prenons l’exemple ci-dessous, serez vous capable d’analyser ce qu’il se passe ?

Cliquez ici pour avoir l’interprétation de l’image.
Une lucarne sur le mur de droite permet aux rayons du soleil d’entrer dans la pièce et de créer une zone très lumineuse sur la porte du réfrigérateur. Nous avons ici une réflexion diffuse, les rayons après avoir touché la porte, rebondissent dans toutes les directions. Les carreaux au sol représentent une surface brillante favorisant la réflexion spéculaire. Ainsi les rayons en provenance de la zone lumineuse sur le réfrigérateur rebondissent sur les carreaux au sol pour atteindre la position de l’appareil photo.
Principe de la réflexion spéculaire
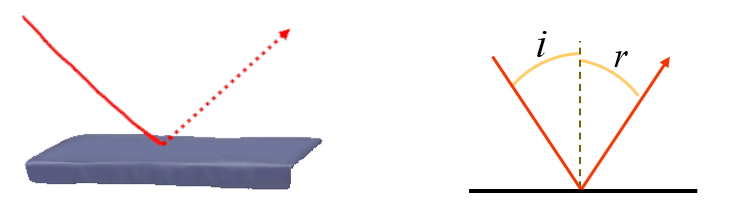
La modèle de réflexion spéculaire correspond à celui du miroir parfait. Un rayon incident rebondit en respectant la loi de Descartes : \(i=r\)
Comportement du spéculaire
Il peut exister dans votre esprit un flou entre l’éclat spéculaire et l’intensité maximale du diffus. En effet, ces deux effets produisent une zone très lumineuse sur un objet. Comment savoir quelle type de réflexion est à l’origine de la tâche lumineuse ? Au premier abord, la réponse n’est pas évidente. Cependant, une différence importante existe : lorsque vous bougez l’éclairage diffus ne change pas alors que l’éclat du spéculaire va lui se déplacer.
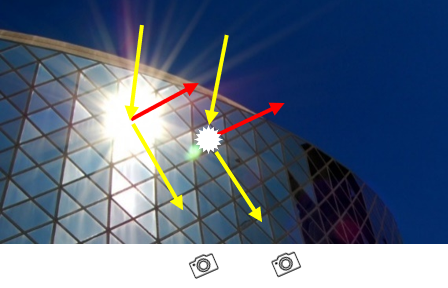
Si nous éxaminons les vitres de ce bâtiment, seulement certaines vont produire l’effet spéculaire. Il s’agit des vitrages se trouvant à la position précise où les rayons du soleil rebondissent pour finir leur course dans l’objectif de l’appareil photo. Si la caméra se déplace légèrement sur la droite, les rayons précédents ne peuvent plus l’atteindre. L’éclat présent à l’ancienne position n’existe plus. L’éclat s’est déplacé et sa position correspond à l’endroit faisant rebondir les rayons lumineux directement vers la nouvelle position de l’appareil photo.
La logique est la même lorsque vous regardez quelqu’un ouvrir une fenêtre dans un bâtiment au loin. A un bref instant, il va y avoir un flash de lumière. Cela correspond au moment où la vitre atteint la position de miroir parfait où elle renvoie les rayons du soleil en direction de votre œil. Une fois cette position dépassée, le flash disparaît.
Calcul du spéculaire
Etape 1 : calcul du rayon réfléchi
Pour calculer l’effet du spéculaire, il faut connaître la direction du rayon réfléchi R :
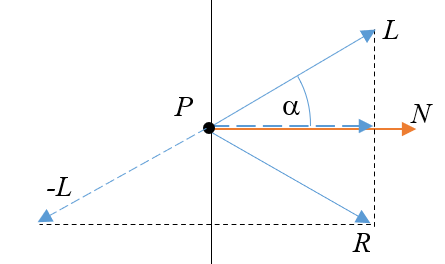
Nous supposons que les vecteurs \(L\) et \(N\) sont des vecteurs normalisés et nous désignons par \(\alpha\) l’angle entre ces deux vecteurs. La projection de \(L\) sur la normale s’obtient facilement avec l’expression \(cos(\alpha).N\). Pour calculer \(R\) la direction du rayon réfléchi, il suffit de remarquer qu’il s’écrit à partir de la combinaison du vecteur \(cos(\alpha).N\) et du vecteur \(–L\).
Etape 2 : position de l’observateur
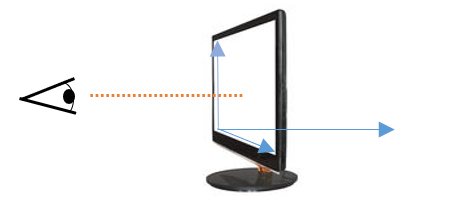
Dans la suite, nous allons avoir besoin de la position de l’observateur dans la scène. Nous travaillons dans le repère de la grille de l’écran : 1 unité = 1 pixel. Il faut donc donner une position pour votre œil dans ce repère. Fournir une coordonnée en pixels à votre œil semble un peu déroutant mais c’est une manipulation assez simple en fait. En effet, vous êtes placé en face de l’écran et votre œil regarde vers le centre de l’écran. Si votre fenêtre d’affichage a une dimension de 2000x1000 pixels, le centre se trouve à la position 1000 et 500. Si l’on considère que vous êtes reculé d’une distance de 1.5x la largeur écran, votre œil est environ reculé à la position 3000. En utilisant les axes de la scène 3D, déduisez la position de la caméra dans la scène. Ce calcul est important car il nous permet d’obtenir des spéculaires réalistes.
Etape 3 : déterminer le paramètre en cos
Si nous connaissons la position de l’observateur et la position du point courant, nous pouvons en déduire la direction \(D\) pointant du point courant vers l’observateur. Le vecteur \(D\) doit être normalisé pour simplifier les calculs. Pour savoir si l’effet spéculaire est présent, il faut connaître l’angle \(\beta\) entre le rayon réfléchi \(R\) et la direction de l’observateur \(D\). Si \(R\) et \(D\) sont colinéaires alors l’angle \(\beta\) est nul et l’effet du spéculaire est présent. Lorsque la caméra/l’observateur se décale de la direction du rebond idéal, l’effet du spéculaire diminue rapidement.
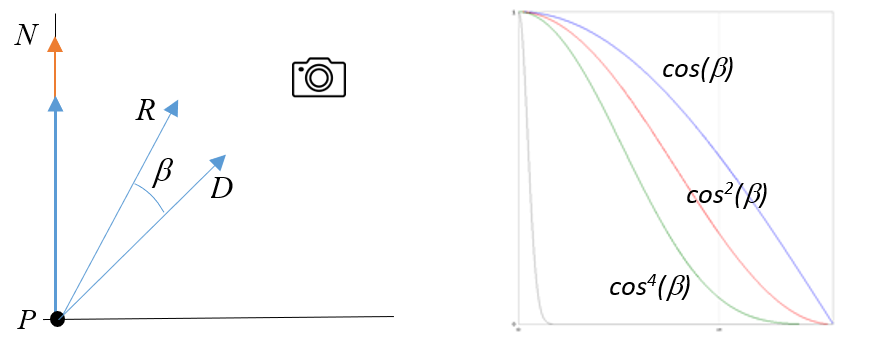
Calculer la valeur exacte de l’angle \(\beta\) est coûteux. Nous devons trouver une astuce pour l’éviter. Si nous examinons la courbe de la fonction \(cos(\beta)\) entre 0° et 90°, nous constatons qu’elle décroît lentement. Nous recherchons une fonction valant 1 lorsque l’angle est proche de 0° et diminuant très rapidement lorsque l’angle augmente. En examinant les courbes des fonctions \(cos^2(\beta)\) puis de \(cos^4(\beta)\), nous constatons que nous obtenons une courbe qui se rapproche de plus en plus de ce que l’on recherche.
Ainsi, nous allons choisir un coefficient \(k\) appelé specular power. Son utilisation est purement pragmatique. Plus la valeur de \(k\) est grande, plus l’éclat du spéculaire sera mince. Usuellement, on choisit pour \(k\) une valeur entre 50 et 200.
Formule du spéculaire
L’effet spéculaire se formule de la manière suivante :
Calcul du spéculaire : \(Coul_{Source}\times (R.D)^k\)
Mise en place
La source lumineuse sera placée en haut à droite avec un éclairage de face. Ainsi, le vecteur lumière L sera égal à (1,-1,1)/√3.
Travail à effectuer Implémentez le modèle spéculaire sur la sphère.
La modèle de Phong incluant l’ambiant, le diffus et le spéculaire est maintenant complet. Suivant le principe d’additivité des rayons lumineux, cumulez la contribution des différents effets pour construire le modèle de Phong appliqué à la sphère. Voici l’image de référence que vous devez obtenir :
