Amélioration du moteur 3D
Virtual Point Lights
La méthode des Virtual Point Lights permet de simuler des rayons lumineux de niveau 2 ceci en utilisant le moteur actuel qui sait traiter les lampes et les rayons lumineux de niveau 1. Pour cela, nous effectuons un traitement en 2 temps :
Etape 1 : considérons chaque source lumineuse et lançons aléatoirement depuis cette source des rayons lumineux dans la scène. Chaque rayon va heurter un objet. Nous calculons alors la couleur associée. L’astuce consiste à transformer cette intersection en une lampe ponctuelle pour simuler des rayons lumineux de niveau 2.
Etape 2 : nous lançons le calcul de la scène en utilisant les lampes pré-existantes et les VPL annexes ceci en utilisant uniquement le modèle d’illumination de niveau 1 habituel. Nous allons ainsi arriver à simuler un éclairage de niveau 2.
En production, on peut aller jusqu’à la création de 100 000 VPL. Il faudra régler cette valeur en fonction des capacités de la machine que vous utilisez.

Remarquez la présence de dégradés dans la luminosité.
PathTracing
Dans le modèle d’illumination diffus de niveau 1, on ne considère que la contribution des rayons lumineux issus des lampes. Cependant, les rayons lumineux proviennent de toutes les zones de la scène ! Pour améliorer notre modèle diffus, pour chaque point 3D traité sur un objet, nous moyennons les contributions des rayons lumineux provenant de directions aléatoires. Voici l’algorithme de principe :
- Calcul du diffus - méthode PathTracer
Depuis le point P courant issu de l’intersection entre un objet et un rayon issu de la caméra
Calculer N la normale locale
Diffus = Couleur(0,0,0)
Pour i = 1 à nb_échantillons
Trouver un vecteur unitaire aléatoire R tq N.R > 0 (le vecteur est orienté vers l’extérieur)
Lancer le rayon R et rechercher son intersection I
(OBJ) Si I est situé sur un objet alors C = couleur de l’objet (diffus de niv 1 + spéculaire de niv 1)
(LMP) Si I est situé sur une lampe : C = couleur de la lampe
Diffus += (N.R)*C
Diffus /= n
Retourner Diffus
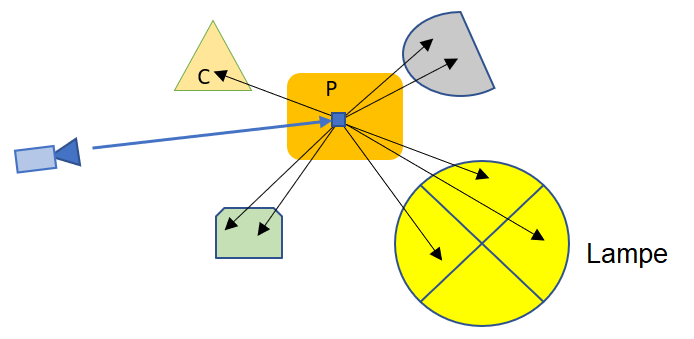
Dans le modèle du PathTracing, les lampes doivent être associées à des objets de la scène (par une sphère ou un rectangle). La puissance totale d’une lampe et donnée par sa couleur multipliée par sa surface ! En effet plus une lampe est large, plus de rayons vont aller la toucher et plus elle va contribuer à l’éclairage du point courant. Ainsi lorsque vous changer la taille d’un rectangle modélisant une lampe, vous allez constater une augmentation de la luminosité globale de la scène.
Contribution des lampes
Dans l’algorithme précédent, on conserve la ligne (LMP) et on désactive la ligne (OBJ). Ainsi, les rayons vont apporter une contribution uniquement s’ils touchent une des lampes au plafond. De cette façon, le bas des boules n’est pas éclairé car les rayons lancés depuis cet endroit n’atteignent pas les lampes.

Contribution des objets
Dans l’algorithme précédent, on conserve la ligne (OBJ) et on désactive la ligne (LMP). Ainsi, les rayons vont apporter une contribution uniquement s’ils touchent un objet. On analyse donc la contribution des éclairages de niveau 2. Le sol est absent car tous les rayons du pathtracer relancé depuis le sol n’atteigne aucun endroit éclairé directement par une lampe. Par contre, le bas des boules apparaît cette fois éclairé. En effet, il s’agit de l’éclairage indirect provenant du sol (niv 2), sol qui lui est directement éclairé par les lampes (niv 1).

Spéculaires de niv 1
On peut calculer, comme dans la partie I, les spéculaires de niveau 1.

Rendu final
En cumulant les trois résultats précédents, nous obtenons l’image suivante :

Notez le grain qui apparaît dans l’image est typique de la méthode du Pathtracing. Pour le faire diminuer, il faut augmenter le nombre d’échantillons utilisés dans l’algorithme. Mais, multiplier par 10 le nombre de rayons relancés implique que la méthode prenne 10 fois plus de temps !
Raytracer
Le Raytracer est une approche intéressante. Très à la mode dans les années 90/2000, elle permet de représenter des réflexions et des réfractions complexes tout à fait impressionnantes. Cette méthode est basée sur la récursivité. Lorsqu’un point d’intersection est trouvé entre un rayon et un objet, nous calculons sa couleur de la manière suivante :
Ainsi un rayon qui heurte une surface déclenche comme dans le moteur de la partie I le calcul du Diff/Spec/Amb habituel. Ensuite, deux nouveaux lancés de rayons peut être générées depuis le point courant : un pour la réflexion (si l’objet est brillant) et un pour la réfraction (si l’objet est transparent). La direction du rayon réfléchi se construit par la loi de Descartes avec la symétrie autour du vecteur normal comme nous avons déjà étudiée dans la partie I.
Pour les surfaces transparentes, la direction du rayon réfracté se déduit à partir de la loi de Fresnel : \(n_1 \sin i_1 = n_2 \sin i_2\) où n désigne l’indice de Fresnel du matériau concerné. Pour appliquer la formule de Fresnel, il faut connaître la matière d’origine et la matière que va ensuite traverser le rayon. Voici quelques valeurs utiles :

Les coefficients \(\rho_1\) et \(\rho_1\) sont dans [0,1]. Ils indiquent si le matériau est pas (=0), peu, très ou totalement (=1) réfléchissant ou transparent.
Le danger dans cette approche peut être l’explosion exponentielle due à la récursivité. Si la scène contient une multitude d’objets transparents et brillants, le rayon initial va générer 2 puis 4 puis 8 puis … trop de rayons. Pour éviter cela, on met une borne sur la profondeur maximale de la récursivité (3,4,5 ou 6) ce qui règle ce problème.
Pour rendre hommage aux générations d’ESIEEns s’étant illustrés dans le projet de synthèse d’image, voici quelques exemples des leurs créations :





Génération aléatoire de directions
Pour les méthodes VPL et Pathtracer, vous devez générer une direction aléatoirement. Pour cela, certains d’entre vous vont utiliser les coordonnées sphériques : tirage aléatoire des valeurs u et v et calcul d’une direction. Une telle approche conduit à une distribution incorrecte des vecteurs sur la sphère unitaire :

En effet, le problème se situe près des pôles. Si l’on prend la zone [0°,360°]x[85°,90°] (le pôle nord) comparée à la zone [0°,360°]x[-2.5°,2.5°] (l’équateur), nous allons statistiquement générer la même quantité de vecteurs. Cependant, sur une surface très petite (le pôle) comparée à une surface plus grande autours de l’équateur, il y aura donc une densité supérieure sur la région des pôles. Nous aimerions avoir une densité uniforme de ce type :

Ce problème s’avère être un problème difficile des mathématiques. Il n’y a pas de méthode idéale. Cependant, au vue des besoins, des méthodes approchées virent le jour permettant de construire de bons résultats. Nous vous donnons la fonction suivante, afin d’optimiser les temps de calcul, vous pourrez précalculer un set d’échantillons assez importants en début de programme. Attention à le parcourir en intégralité et à ne pas toujours repartir du premier dans la liste.
for(int i = 0 ; i < nb ; i++)
{
double theta = 2*PI*rand(0.0,1.0);
double phi = acos(2*rand(0.0,1.0)-1.0);
x[i] = cos(theta)*sin(phi);
y[i] = sin(theta)*sin(phi);
z[i] = cos(phi);
}