La librarie G2D

Build du projet

Téléchargement & Compilation

Téléchargez et décompressez La librairie G2D.

Visual Studio

Double-cliquez sur le fichier G2D.sln ce qui ouvre le projet dans Visual Studio.

Dans l’explorateur de solutions, dépliez les sections Header Files et Source Files comme ceci :

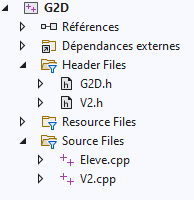
Vous remarquez les quatre principaux fichiers avec lesquels vous allez travailler :

G2D.h : contient les déclarations des fonctions de la librairies G2D, c’est presque une documentation.

Eleves.cpp : contient le code de votre projet, c’est le seul fichier que vous allez éditer.

V2.h et V2.cpp : les deux fichiers qui fournissent la structure vecteur V2 et ses opérateurs surchargés.

Et :

Vérifiez dans le bandeau en haut que vous êtes en mode Debug x86 :

Puis :

Lancez le programme en appuyant sur la touche F5.

Vous devez voir apparaître le texte « Hello World! » à l’écran.

Appuyez sur la touche P pour mettre en pause l’application.

Appuyez sur la touche ESC pour fermer l’application.

Linux / Ubuntu / Debian

Voici les étapes à effectuer :

Après avoir décompressé les fichiers, vous pouvez supprimer les fichiers propres à Windows et Visual (*.dll, *.lib, vcxproj, *.sln).

Ouvrez une fenêtre terminal et rendez-vous dans le répertoire en question.

Dans le shell, lancez la commande suivante : g++ *.cpp -lGL -lGLU -lglut

Vous aurez peut-être un message d’erreur vous indiquant que des paquets sont indisponibles.

Dans ce cas, installez les éléments suivants : sudo apt-get install mesa-utils freeglut3-dev freeglut3

Une fois la compilation réussie, tapez dans le shell : ./a.out

Vous devez voir une petite animation à l’écran.

Appuyez sur la touche ESC pour fermer l’application.

MacOS Monterey

Voici les étapes à effectuer :

Ouvrez une fenêtre terminal (Applications/Utilitaires/Terminal), nous vous conseillons d’ailleurs de la docker.

Dans le terminal, tapez : g++ suivie de la touche Entrée, l’OS vous propose alors d’installer g++ (30 minutes).

Dans le terminal, tapez : g++ --version, vous devriez obtenir : Apple clang …

Décompressez le projet.

Supprimez les fichiers propres à Windows et Visual (*.dll, *.lib, vcxproj, *.sln).

Lancez la compilation avec la commande : g++ *.cpp -std=c++11 -w -framework GLUT -framework OpenGL -framework Cocoa

Lancez le programme en tapant dans le terminal : ./a.out

Vous devez voir une petite animation à l’écran.

Appuyez sur la touche ESC pour fermer l’application.

Lancez la démo

Lancez le programme, vous devez obtenir l’affichage suivant :

Un texte est affiché en rouge

Un segment tourne sur lui-même à vitesse constante

Une boule rouge se déplace sur la droite en bas de la fenêtre

Le curseur de la souris correspond à une croix blanche

Si vous cliquez sur le bouton gauche de la souris, un rond s’affiche au centre du curseur

Point / Vecteur

La structure V2

Un programme traitant des affichages graphiques 2D contient de nombreuses variables de la forme : x, y, xx, yy, tx, ty… Pour éviter cela, nous préférons mettre en place une structure V2 permettant de stocker des coordonnées (x,y). Ouvrez le fichier V2.h. Nous y trouvons la définition suivante :

struct V2
{
    float x, y;

    V2()                    { }
    V2(float _x, float _y)  { x = _x; y = _y; }

    float   norm()          { return sqrt(x*x + y * y); }
    void    normalize()     { float n = norm();     x /= n;    y /= n;    }
    V2      GetNormalized() { float n = norm();  return V2(x/n,y/n); }
};

Les coordonnées x et y sont stockées en float. En effet, le type float permet tout aussi bien de représenter des valeurs entières que des nombres à virgule, nous les choisissons donc pour leur polyvalence. Un constructeur est fourni pour initialiser un objet à partir de deux valeurs x et y ainsi qu’un constructeur par défaut. La fonction norm() retourne la norme du vecteur associé et la fonction normalize() le normalise.

Note

Cette classe stocke deux valeurs, elle peut donc aussi bien représenter les paramètres d’un vecteur ou les coordonnées d’un point.

Les opérateurs

Le langage C++ nous permet de définir le fonctionnement des opérateurs + - * … sur de nouvelles classes. On appelle ce mécanisme la surcharge d’opérateurs. Ainsi, pour la classe V2, nous trouvons comme opérateurs surchargés dans le fichier V2.h.

V2 operator + (const V2 & a, const V2 & b);
V2 operator - (const V2 & a, const V2 & b);
V2 operator * (float      a, const V2 & b);
V2 operator * (const V2 & a, float      b);
V2 operator / (const V2 & a, float      b);
V2 operator - (const V2 & a);

Note

L’usage veut que les opérateurs acceptent des const référence en entrée afin d’accepter des rvalues. Chaque opérateur retourne un objet et non une référence sur un objet temporaire (local) ce qui serait dangereux.

Les définitions de ces surcharges se trouvent dans le fichier V2.cpp. Par exemple, la surcharge de l’opérateur binaire + correspond à :

V2 operator + (const V2 & a, const V2 & b)
{
    return V2(a.x + b.x, a.y + b.y);
}

Cette écriture compacte est équivalente à l’écriture suivante :

V2 operator + (const V2 & a, const V2 & b)
{
        V2 temp = V2(a.x + b.x, a.y + b.y)
        return temp;
}

Produit scalaire / vectoriel

Deux fonctions permettent de calculer le produit scalaire et le produit vectoriel entre deux V2 :

float prodScal(const V2 & a, const V2 & b) { return a.x * b.x + a.y * b.y; }

float prodVect(const V2 & a, const V2 & b) { return a.x * b.y - a.y * b.x; }

Avertissement

Le produit scalaire retourne un scalaire ! Ici, ce sera donc un flottant. En 3D et en n-dimensions, le produit vectoriel retourne un vecteur, mais en 2D, il retourne cette fois un scalaire. En effet, le produit vectoriel de deux vecteurs dans le plan devrait donner un vecteur vertical de la forme (0,0,z) mais ce dernier n’appartient pas au plan ! Ainsi, par convention, dans le cas 2D, on retourne seulement la composante en z de ce vecteur en guise de résultat.

Affichage

L’opérateur << a été surchargé pour permettre l’affichage d’un objet V2 en utilisant un cout. L’objet cout étant de type ostream (output stream), voici la déclaration de la surcharge de cet opérateur :

std::ostream & operator << ( std::ostream & os, V2 & t );

Petit rappel. L’opérateur binaire << dans l’écriture : cout << 5 s’interprète comme l’opérateur + dans l’écriture a+b. Son opérande gauche est l’objet cout de type ostream et son opérande droite est un objet de type V2. Pour obtenir un affichage de la forme (4,12), voici le code correspondant :

ostream & operator << (ostream & os, V2 & t)
{
        os << "(" << t.x << "," << t.y << ")";
        return os;
}

Pourquoi retourner un objet de type ostream & ? Tout simplement pour chaîner plusieurs opérateurs << comme dans l’écriture cout << a << » » << 5;.

Exemple

Dans le fichier eleve.cpp, au début de la fonction main(), insérez le code suivant et exécutez le :

V2 A(5,10);
V2 B = V2(6,15);
V2 AB = B - A;
cout << AB << endl;

Comment décoder ces lignes :

La première ligne correspond à la création d’un point A par appel au constructeur paramétrique.

La deuxième ligne est une variante de la première.

La troisième ligne calcule le vecteur AB.

Note

Comment fonctionne la ligne V2 AB = B - A; ? L’opérateur - effectue la soustraction entre A et B et retourne un objet temporaire. Cet objet temporaire (sans nom) est utilisé comme rvalue de l’opérateur = pour initialiser l’objet AB nouvellement créé.

En exécutant cet exemple, l’affiche dans la console doit donner : (1,5)

Travail à effectuer

A la suite du code précédent, effectuez les traitements suivants :

Définissez trois points A=(1,2), B=(0,5) et C=(7,3).
Calculez les vecteurs AB et AC ainsi que leur produit scalaire et leur produit vectoriel.
Affichez la norme du vecteur AB.
Normalisez le vecteur AB et affichez-le, calculez sa norme et vérifiez qu’elle est égale à 1.

La librairie graphique 2D : G2D

Cette librairie a été conçue spécialement pour vos projets afin d’être efficaces, multi-plateformes et simple d’utilisation tout en requérant très peu de dépendances.

La couleur

En image, les couleurs sont décrites suivant trois composantes : le rouge, le vert et le bleu. Les valeurs de chaque composante peuvent être représentées soit par un nombre flottant dans l’intervalle [0,1] soit par une valeur entière allant de 0 à 255. Ces deux représentations sont, à notre niveau, totalement équivalentes. Il existence un quatrième paramètre codant la transparence (alpha). Nous l’utiliserons plus tard dans les projets.

Les différents moyens d’obtenir un objet Color :

Color(1,1,1) : par appel du constructeur de la classe Color avec des valeurs dans l’intervalle [0,1].

Color::Cyan : par utilisation d’un objet Color prédéfini dans le fichier G2DColor.cpp.

ColorFrom255(255,255,255) : par appel d’une fonction prenant 3 paramètres RGB codés de 0 à 255.

ColorFromHex(0xf28f93) : par appel d’une fonction prenant le code couleur en hexadécimal.

On peut trouver les codes couleurs en utilisant :

Le nuancier wikipedia en plaçant le curseur de la souris sur la couleur choisie.

L’outil ColorPicker

Le repère cartésien

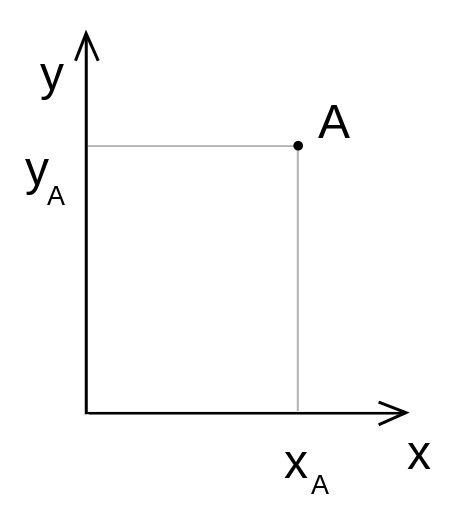
Comme vous êtes très habitués au repère cartésien, les coordonnées de l’écran seront donc données dans ce repère :

Origine (0,0) en bas à gauche

Axe des abscisses horizontal et orienté vers la droite

Axe des ordonnées vertical et orienté vers le haut

Note

Très souvent en graphisme, on utilise un autre repère avec l’origine en haut à gauche et l’axe des ordonnées orienté vers le bas.

Les fonctions de tracé

L’écriture G2D::MaFnt(…) permet d’accéder aux fonctions fournies par la librairie graphique 2D du projet.

Diverses fonctions de tracé sont disponibles dans G2D.h :

// Draw Geometry
void setPixel(V2 P, Color c);
void drawLine(V2 P1, V2 P2, Color c );
void drawRectangle( V2 P1, V2 Size, Color c, bool fill = false);
void drawCircle(V2 C, float r, Color c,  bool fill=false);

// draw string
void drawStringFontMono (V2 pos, std::string text, float fontSize = 20, float thickness = 3, Color c = Color::Black);

Pour les fonctions de tracé, on trouve principalement :

setPixel(…) : positionne la couleur d’un pixel de l’écran

drawLine(…) : dessine un segment entre deux points et avec une couleur donnée.

drawRectangle(…) : dessine un rectangle avec des bords horizontaux et verticaux. Pour cela, on fournit les coordonnées (xmin,ymin) du sommet en bas à gauche, la hauteur/largeur, la couleur choisie et un booléen indiquant si le rectangle est plein.

drawCircle(…) : dessine un cercle. Pour cela, on fournit les coordonnées du centre, le rayon et un booléen indiquant si le cercle est plein.

drawStringFontMono(…) : écrit un texte à une position donnée avec une taille fontsize, une épaisseur thickness et une couleur c choisies. Il se peut que le paramètre thickness ne produise pas d’effet sur certaines machines.

Fonction de timing

La fonction ElapsedTimeFromStartSeconds() retourne un nombre flottant indiquant le temps écoulé en secondes depuis le lancement du jeu.

Travail à effectuer

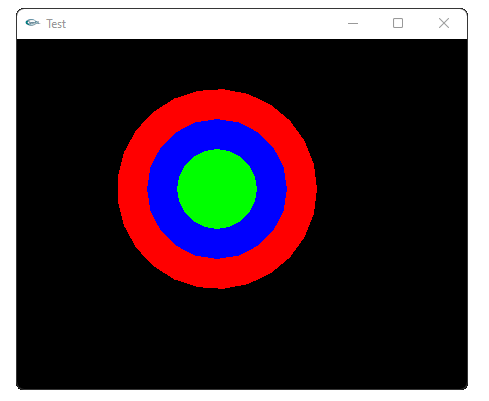
Dans la fonction Render(), ajoutez du code pour tracer trois cercles pleins concentriques :

Le cercle intérieur vert fait 40 pixels de rayon.
Le cercle bleu fait 70 pixels de rayon.
Le plus grand cercle est un cercle rouge de 100 pixels de rayon.
Faites en sorte que cette forme se déplace en suivante le curseur de la souris.

Note

Dans cet exercice, il faut faire attention à l’ordre dans lequel les tracés sont effectués. Dessiner dans la zone d’affichage, c’est comme peindre : le dernier objet dessiné recouvre les autres.