Path Animation

Certains éléments du jeu ont leurs propres IA qui contrôlent leurs déplacements. D’autres sont reliés à un modèle physique, comme la bille du flippeur, permettant de les animer de manière automatique. Cependant, certains éléments, allant des ennemis jusqu’aux papillons du décor ont parfois simplement un parcours à effectuer.

Si vous voulez que vos ennemis ou que vos papillons bougent à l’écran, en faisant autre chose que du gauche/droite, cela requiert un peu d’attention. Pour cela, nous allons présenter la modélisation d’un trajet ainsi que son parcours.

Mise en place d’une path animation

Parcours d’une ligne polygonale

Dans cette configuration, un élément du jeu se déplace en suivant une ligne brisée. Chaque morceau correspondant à un segment, ce problème se ramène donc à gérer un déplacement d’un point A à un point B. Notons T le vecteur AB normalisé et P la position courante. Nous donnons à l’élément une vitesse v en pixels/seconde. La nouvelle position est obtenue en effectuant le calcul habituel : Nouvelle Pos = Pos courante + v * dt * T.

Il faut ensuite détecter si la position courante correspond au point B. Il n’est pas conseillé de faire un test d’égalité car il est peu probable que la position courante corresponde exactement au point B. Pour cela, nous allons utiliser la fonction SameDirection(BA,BP) (consultez le chapitre sur la détection de collision). Si ces deux vecteurs sont orientés dans la même direction, alors le point P se trouve toujours à l’intérieur du segment [AB]. S’ils sont orientés en sens inverse, alors le point P vient de quitter le segment [AB]. Dans ce cas, il faut changer de direction et parcourir un autre segment. Le point B devient alors le dernier point visité et la direction courante doit être mise à jour. Voici l’algorithme de principe :

class PathAnim

        LP     // Liste de points
        idLast // id du dernier point visité
        T      // Vecteur déplacement (normalisé)
        v      // vitesse (float)
        Pos    // Position courante
        Stop = False  // indique si on a atteint la fin du chemin

        NewDirection(idP)  // calcul la trajectoire en partant de ce point
           Pos = LP[idP]
           T = LP[idP+1] - LP[idP]
           T.normalize()
           idLast = idP

        PathAnim(PointList,vitesse)
           v = vitesse
           LP = PointList
           NewDirection(0)

        IsFinished()
                return Stop

        Move(dt)
                if Stop : return
                P = Pos + dt * v * T    // calcul prochaine position
                A = LP[idLast]          // dernier sommet visité
                B = LP[idLast+1]        // cible
                if  SameDirection(BA,BP)   // voir page Detection de collision
                    Pos = P                // on avance
                else                       // sinon cible atteinte
                        if idLast != LP.size()-2
                                NewDirection(idLast+1)
                        else
                                Stop = True

Voici le résultat obtenu pour simuler un parcours automatique du vaisseau. La ligne polygonale symbolisant la trajectoire à parcourir est dessinée en vert :

Smooth

La trajectoire sous forme de lignes brisées ne parait pas naturelle. On pourrait utiliser un modèle plus complexe pour modéliser des courbes polynomiales. Mais cela va engendrer beaucoup de calculs et pas mal de code à écrire sans compter les cas particuliers à gérer.

Nous allons choisir de conserver l’algorithme précédent qui a le mérite d’être court et efficace et nous allons attaquer le problème sous un autre angle. Plutôt que de construire un algorithme complexe, nous choisissons d’appliquer un lissage géométrique de la ligne polygonale. L’algorithme associé, appelé Chaikin, est relativement simple et permet d’obtenir un résultat de qualité.

L’algorithme Chaikin utilise l’idée suivante : pour chaque segment de la ligne polygonale en entrée, on crée deux points, placés à 1/4 et à 3/4 de distance des extrémités qui sont ajoutés à la nouvelle ligne polygonale.

Voici l’algorithme de principe :

fnt Smooth(LP):

        SmoothLP = []  // new list of points

        for i from 0 to LP.size()-2
                A = LP[i]
                B = LP[i+1]
                float c1 = 0.25
                float c2 = 0.75
                E = A * c2 + B * c1
                F = A * c1 + B * c2
                SmoothLP.append(E)
                SmoothLP.append(F)

        return SmoothLP

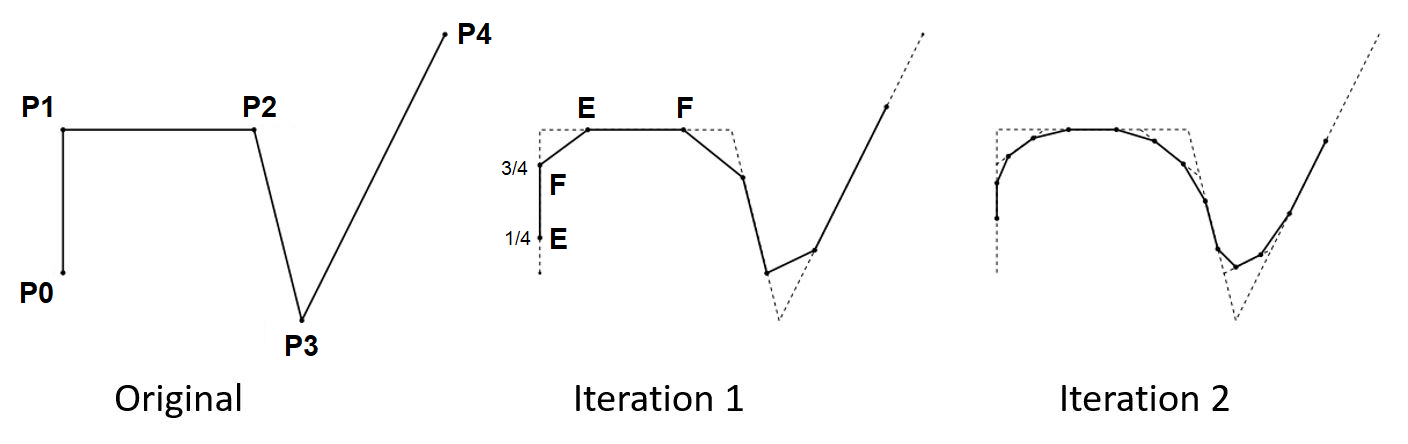
En itérant une deuxième fois, la ligne polygonale devient encore plus lisse (smooth), sa courbure devient plus douce : il y a moins de variation de la direction au niveau des passages aux sommets. Voici l’animation obtenue par application de 3 lissages successifs en partant du chemin original comportant 7 points. Voici un exemple :

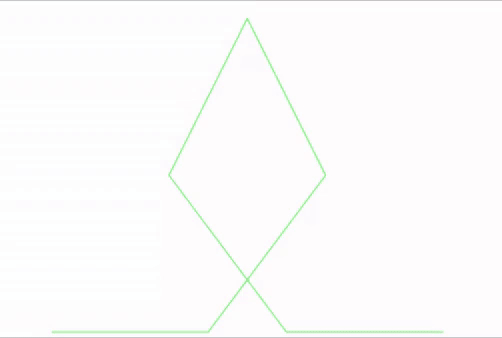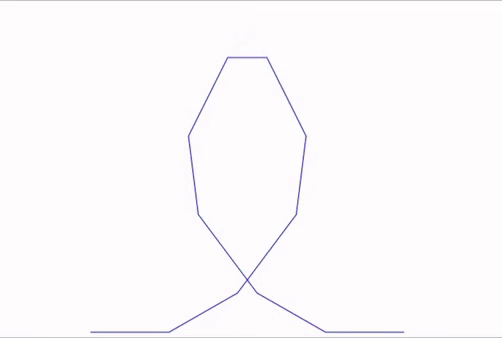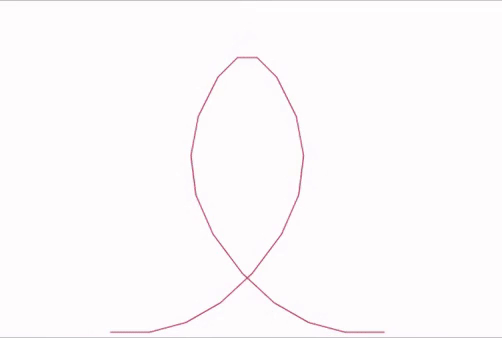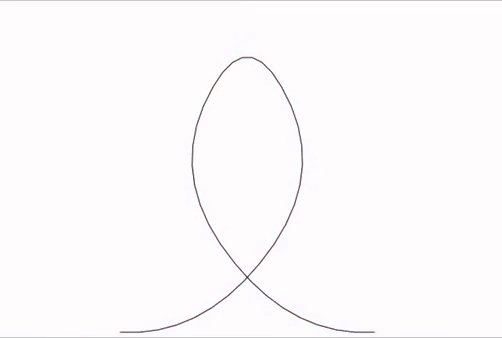
Vous pouvez remarquer que l’animation obtenue en suivant la 4-ième courbe est particulièrement lisse :

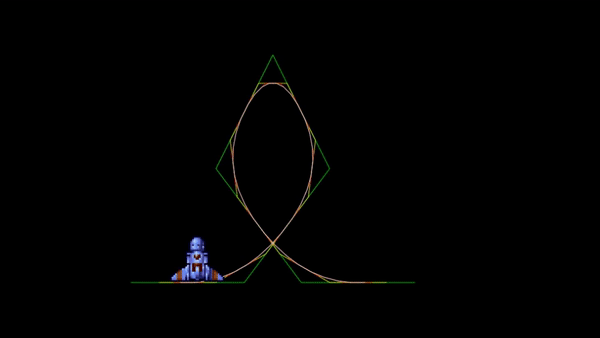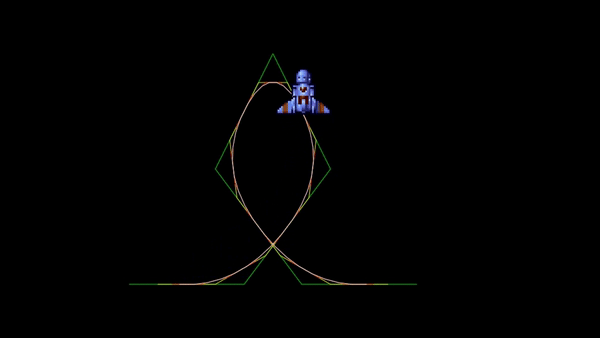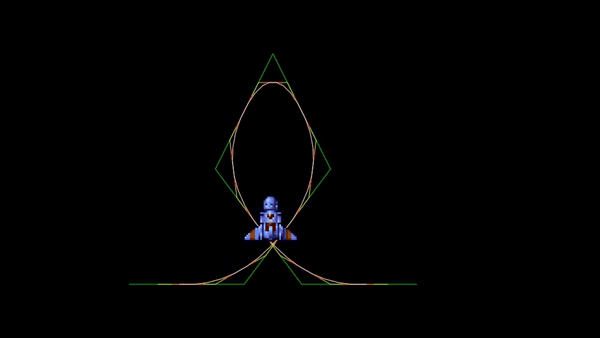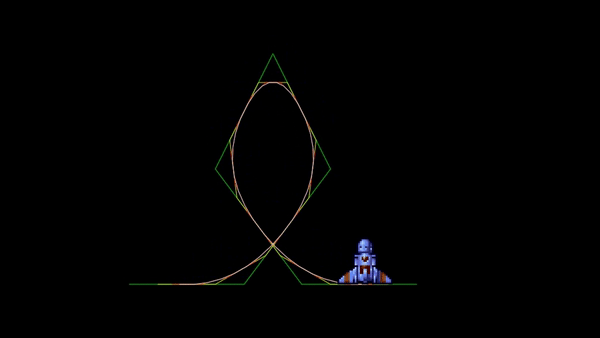
Note

Vous avez peut-être remarqué que l’algorithme de lissage a tendance à rogner les extrémités. Si vous tenez à ce que l’élément démarre à un point précis et termine son trajet à un autre point précis, il vous suffit de réinsérer à chaque application de la méthode le point de départ et le point final dans la nouvelle ligne polygonale.

Pour décrire vos trajets, il suffit donc de décrire votre parcours à partir d’une série de quelques points. L’algorithme de Chaikin se chargera de créer une trajectoire lisse de grande qualité.