TD → Flipper

En premier lieu, téléchargez la librairie G2D sur la page La librairie G2D. Remplacez le fichier Eleve.cpp se trouvant dans le projet par celui-ci.

Téléchargez Le fichier du projet.

Avertissement

La quasi-totalité de votre code doit être écrit dans le fichier Eleve.cpp.

Déplacement

Mise en place

En lançant l’application, vous voyez apparaître le jeu flipper et une bille rouge qui se déplace vers le haut. A ce niveau, la bille traverse les objets du jeu.

Dans les données de jeu, on trouve deux variables :

  • V2 BallPos indiquant la position de la bille.

  • V2 BallMove indiquant le vecteur déplacement appliqué à chaque appel de la fonction logic().

La fonction logic() est appelée 50 fois par seconde, ce nombre étant passé en argument à la fonction Run(..)

G2D::Run(Logic, render, G, 50);

Ainsi avec 50 appels par seconde et un vecteur BallMove initialisé à (0,10), la bille parcourt une distance de 500 pixels par seconde. Pour notre terrain de 650 pixels de haut, cela veut dire que la bille met un peu plus d’une seconde pour le traverser, ce qui est assez réaliste.

Note

Attention si certains veulent augmenter la vitesse de la bille, il ne faut pas donner de valeurs trop grandes au vecteur de déplacement. Faites en sorte que la norme de BallMove reste < 10. En effet, ce vecteur correspond au « saut » effectué par la bille à chaque itération. Une valeur trop grande a pour effet de faire sauter la bille trop loin ce qui peut avoir plusieurs effets inattendus : non détection d’une collision, collisions avec plusieurs objets… Pour accélérer la bille, vous devez augmenter le nombre d’appels par seconde à la fonction logic().

Exercice

Modifiez le code pour faire démarrer la bille de la position (100,100) avec un vecteur de déplacement (10,10). Il n’y pas de rebond avec les objets à ce niveau. Vous devez obtenir le résultat suivant :

../_images/moving.gif

Assistance

Nous avons ajouté une fonctionnalité de Debug qui trace en pointillés les anciennes positions de la bille. Pour cela, nous utilisons une liste de V2 : PreviousPos dans la structure GameData. A chaque déplacement, on empile la nouvelle position et on retire la plus veille de la liste :

G.PreviousPos.push_back(G.BallPos);
G.PreviousPos.erase(G.PreviousPos.begin());

Vous pouvez allonger ou raccourcir ce tracé en faisant varier la taille du buffer initialement fixée à 50 valeurs :

PreviousPos.resize(50);

Simuler un rebond

Nous allons maintenant mettre en place les rebonds de la bille sur les bords de la zone de jeu.

Rappel sur les vecteurs

On obtient les coordonnées du vecteur AB par soustraction des coordonnées de A aux coordonnées de B.

RAPPEL : le vecteur \(\overrightarrow{AB}\) s’obtient en calculant B - A

Dans la suite, il vous est demandé d’utiliser les structures V2 pour décrire les coordonnées de vos points ainsi que les composantes de vos vecteurs.

Les opérateurs surchargés devront aussi être utilisés pour simplifier le code. Il serait très maladroit de réécrire toutes les formules à partir des composantes en x et y. Ainsi, on n’écrira pas : AB.x = B.x - A.x; et AB.y = B.y-A.y. Mais on utilisera les opérateurs surchargés pour écrire une syntaxe proche de l’écriture mathématique :

V2 AB = B - A;

Rebond

Formules

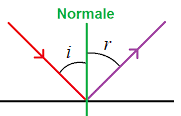
Nous allons étudier le rebond contre un bord de direction quelconque. La loi de Descartes énonce que l’angle i entre la direction incidente et la normale au bord est égal à l’angle r entre la normale et la direction de rebond.

../_images/descartes.png

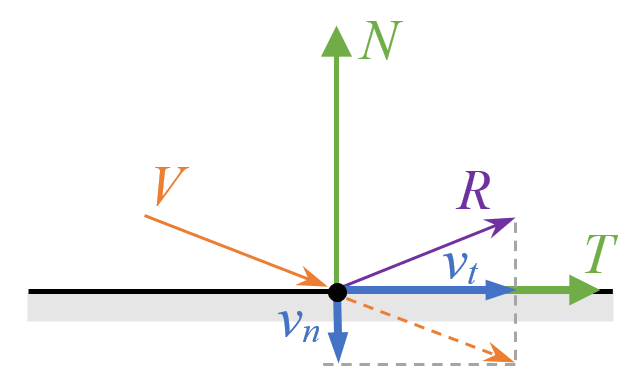
Notons \(N=(n_x,n_y)\) le vecteur normal au bord orienté vers l’extérieur (de l’objet servant de bord). Nous avons besoin pour nos formules que ce vecteur soit normalisé. Notons \(T\) le vecteur correspondant à la rotation de 90° du vecteur \(N\) dans le sens horaire. La direction d’incidence correspond au vecteur de déplacement \(V\) de la bille. Nous cherchons le nouveau vecteur de déplacement \(R\) après le rebond. Si nous connaissons la projection orthogonale de \(V\) sur \(N\) notée \(v_n.N\) et de \(V\) sur \(T\) notée \(v_t.T\), nous constatons que \(R= v_t.T - v_n.N\). Nous remarquons que seule la composante \(v_n\) de \(V\) change de sens lors du rebond :

../_images/rebond.png

Il nous reste à calculer \(v_t\) et \(v_n\) en utilisant les formules classiques. Voici l’algorithme de principe :

function Rebond(V,N):
        N.normalize()
        T  = (ny,-nx)  // rotation de 90° du vecteur n sens horaire
        vt = V * T     // produit scalaire, vt est un nombre
        vn = V * N     // produit scalaire, vn est un nombre
        R = vt * T - vn * N // * entre un flottant et un V2
        return R

Etape de validation

Nous allons utiliser un jeu de tests pour valider l’exactitude de la fonction Rebond(…). Vérifiez que vous obtenez des vecteurs de rebond corrects pour les configurations suivantes :

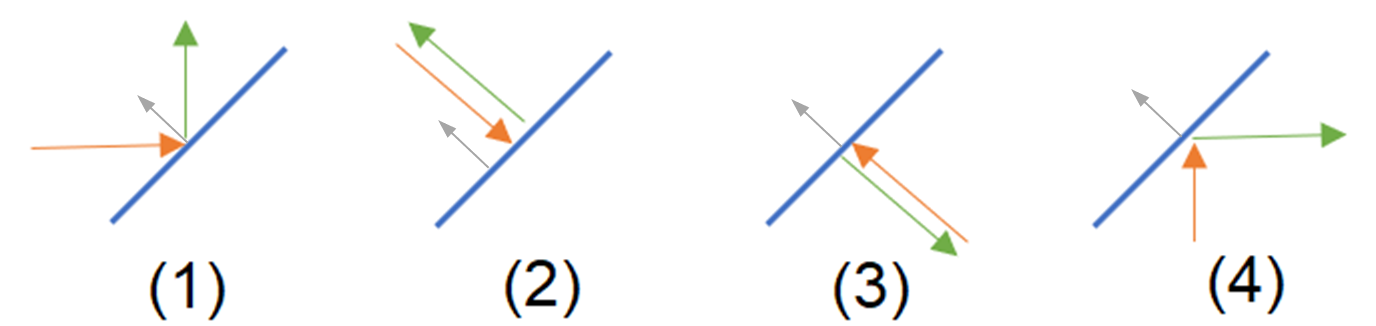
Rebond sur un mur avec un vecteur normal N = (-1,1) :

  • Cas 1 : V=( 1, 0) → R = ( 0, 1)

  • Cas 2 : V=( 1,-1) → R = (-1, 1)

  • Cas 3 : V=(-1, 1) → R = ( 1,-1)

  • Cas 4 : V=( 0, 1) → R = ( 1, 0)

../_images/verif.png

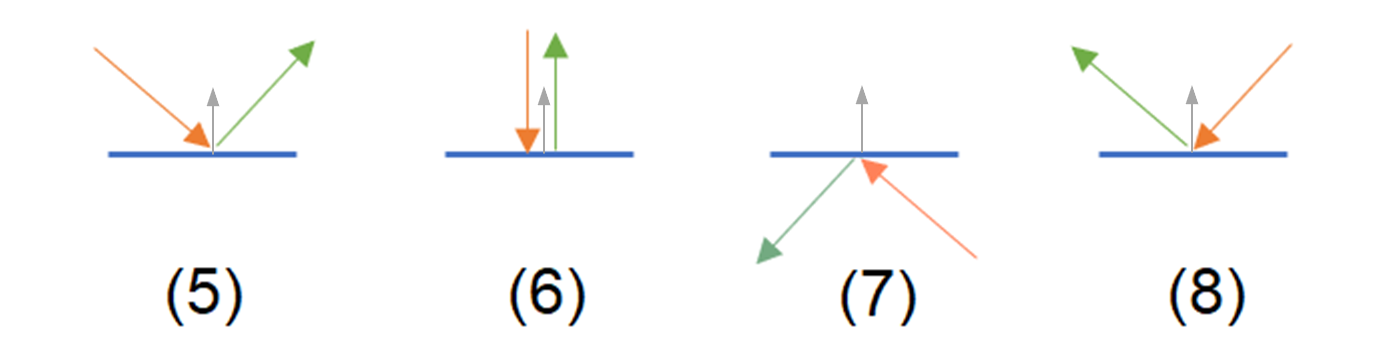
Rebond sur un mur avec un vecteur normal N = (0,1) :

  • Cas 5 : V=( 1, -1) → R = ( 1, 1)

  • Cas 6 : V=( 0, -1) → R = (0, 1)

  • Cas 7 : V=(-1, 1) → R = (-1,-1)

  • Cas 8 : V=(-1, -1) → R = ( -1,1)

../_images/verif2.png

Calcul de la nouvelle position

Nous calculons la nouvelle position de la bille à chaque appel de la fonction Logic() en tenant compte de la position courante et du vecteur de déplacement de la bille. Ainsi, nous obtenons :

\(Nouvelle~Position = Position~Courante + Vecteur~Déplacement\)

Cependant, si la nouvelle position de la bille croise un obstacle, il ne faut pas y aller ! Voici la logique d’un déplacement :

  • Si la nouvelle position est valide, nous déplaçons la bille, exemple : Pos 0 → Pos 1

  • Sinon, exemple : Pos 1 → Pos 2

    • Mettre à jour le vecteur déplacement par simulation du rebond

    • Déplacer ensuite la bille, exemple : Pos 1 → Pos 3

Le comportement obtenu est le suivant :

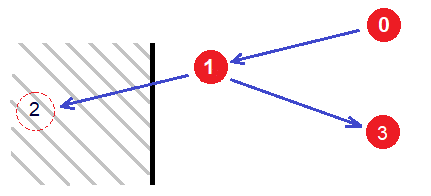
../_images/option2.png

Mise en place

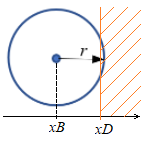
Vous allez maintenant faire rebondir la bille sur les bords de la fenêtre de jeu. Pour tester si la nouvelle position de la bille entre en collision avec un bord de l’écran, il suffit par exemple pour le bord droit de vérifier si l’abscisse de la bille xB est supérieure à l’abscisse du bord droit xD soustrait du rayon de la bille en testant : \(x_B > x_D - r\), voir le schéma ci-dessous :

../_images/borddroit.png

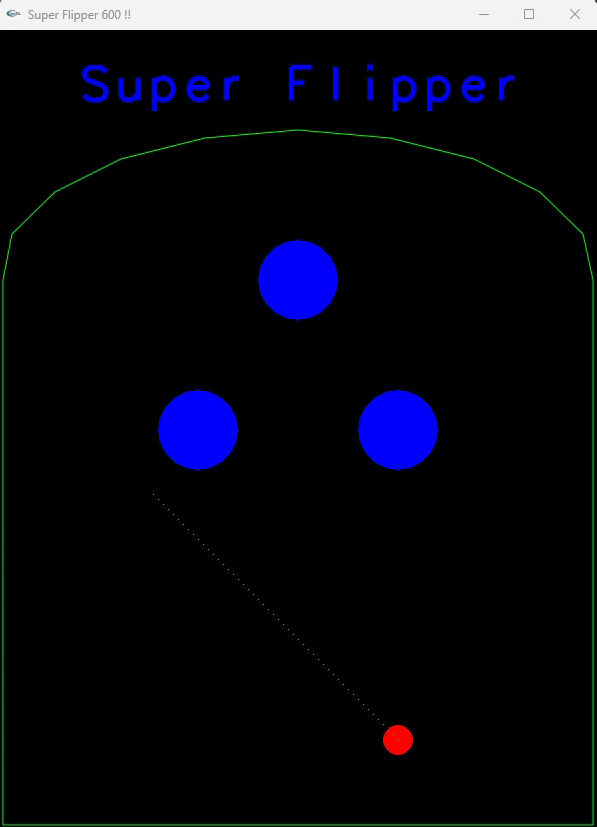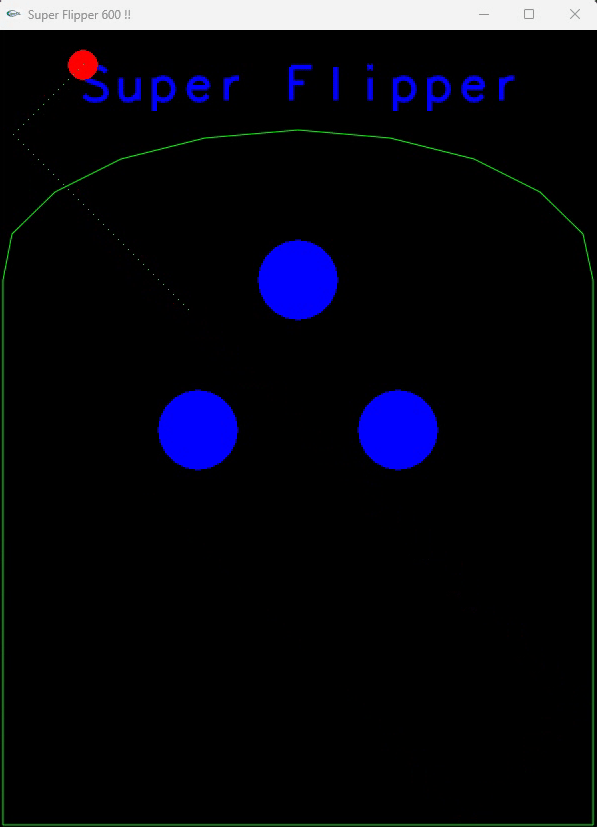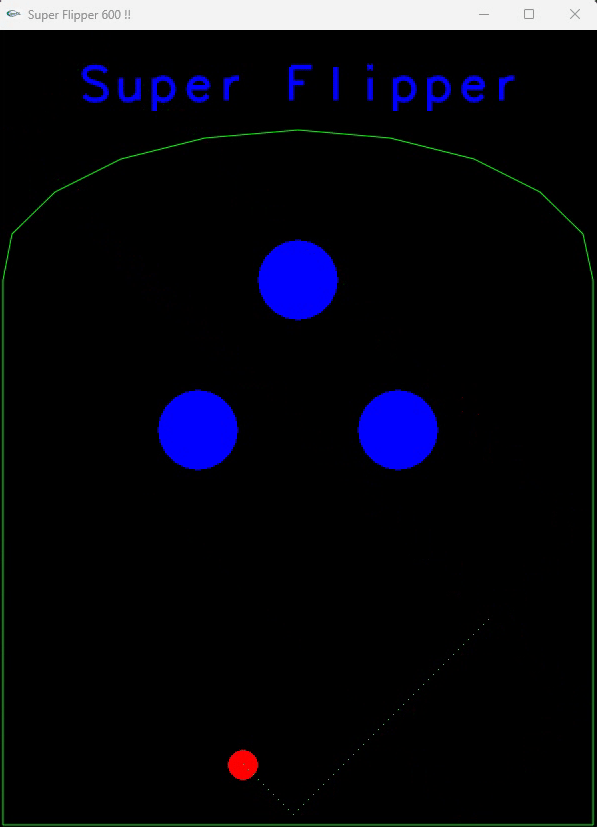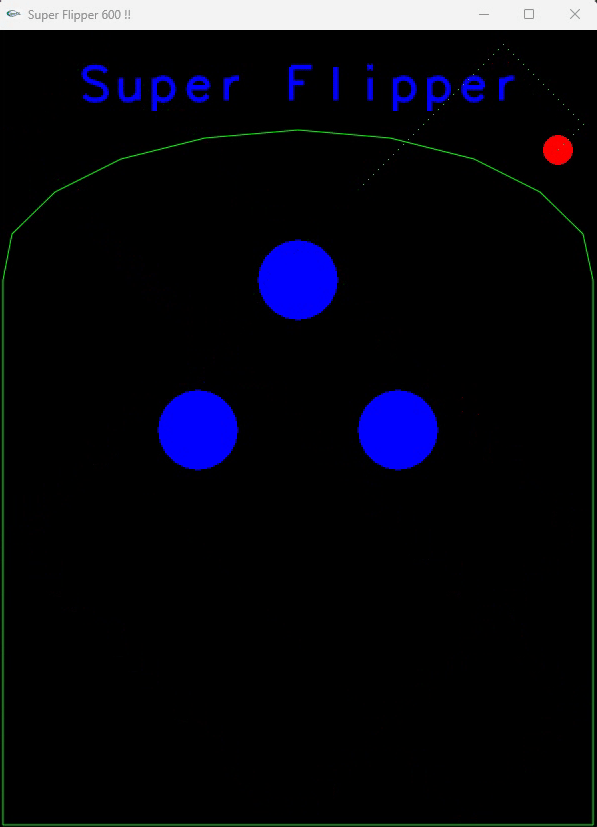
Voici ce que vous devez obtenir :

../_images/rebondsbords.gif

Bords du décor

Nous allons maintenant faire rebondir la bille contre les bords du flipper dessinés en vert. Les bords sont décrits comme une ligne polygonale fermée (une liste de segments) dont les sommets sont stockés dans un objet vector nommée LP.

Collision bille/segment

Lorsque la bille entre en contact avec un segment [AB], trois configurations sont possibles :

  • Cas 1 : la bille tape contre le sommet A

  • Cas 2 : la bille tape sur l’intérieur du segment [AB]

  • Cas 3 : la bille tape contre le sommet B

Chacune de ces trois configurations se gère finalement comme un rebond contre un mur :

  • Cas 1 : simulez un rebond contre un mur virtuel passant par le sommet A et ayant comme direction normale \(B\rightarrow A\)

  • Cas 2 : effectuez un rebond contre un mur virtuel correspondant au segment [AB]

  • Cas 3 : gérez un rebond contre un mur virtuel passant par le sommet B et de direction normale \(A\rightarrow B\)

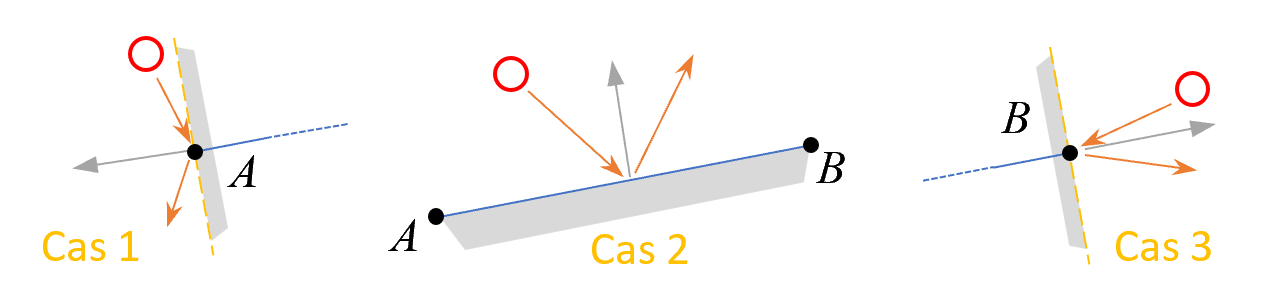
../_images/zonesbille.png

Dans le code, la fonction int CollisionSegCir(V2 A, V2 B, float r, V2 C) est fournie et retourne une valeur indiquant la configuration dans laquelle a lieu la collision.

Collision sur les bords

Pour détecter la collision de la bille avec un des segments du bord, nous allons parcourir la liste des sommets et vérifier si la nouvelle position de la bille intersecte les côtés correspondants. Comme les segments sont juxtaposés, nous ne traiterons que le cas de l’intersection se produisant dans la zone 2.

Voici le résultat que vous devez obtenir :

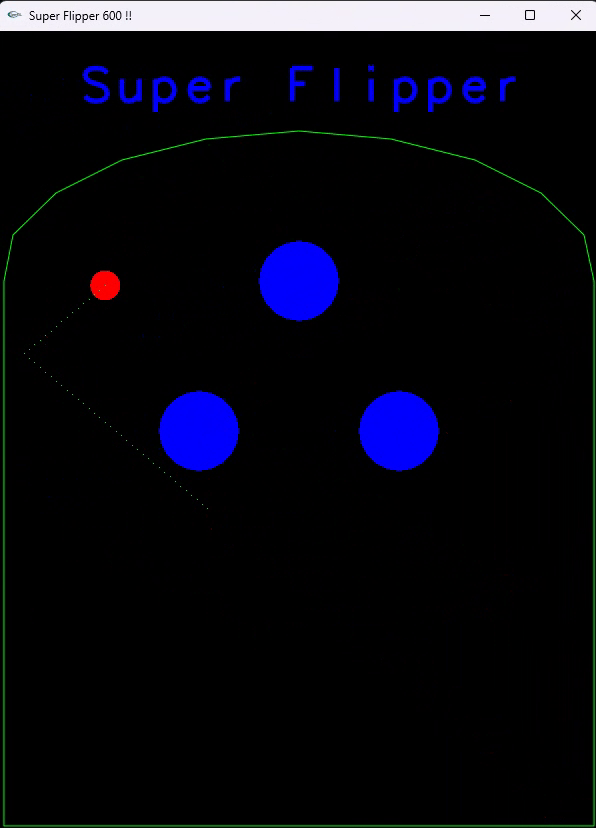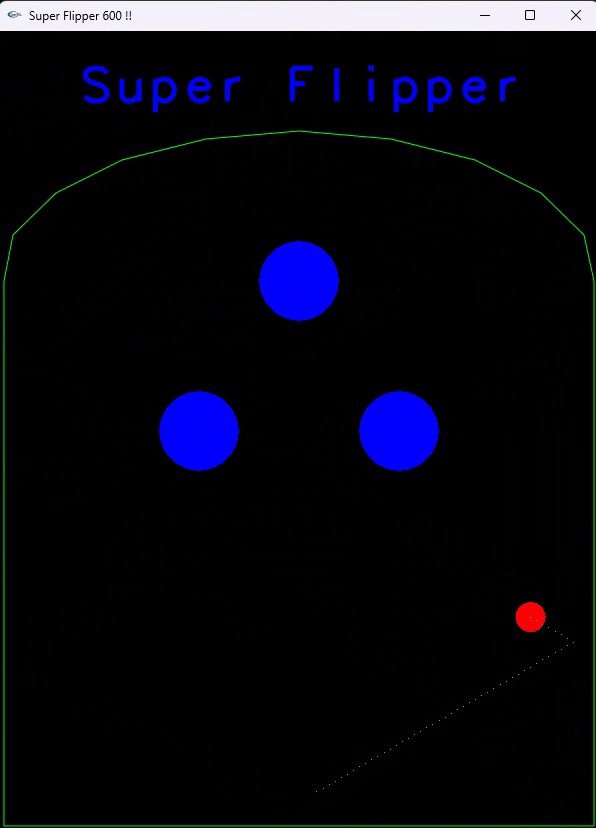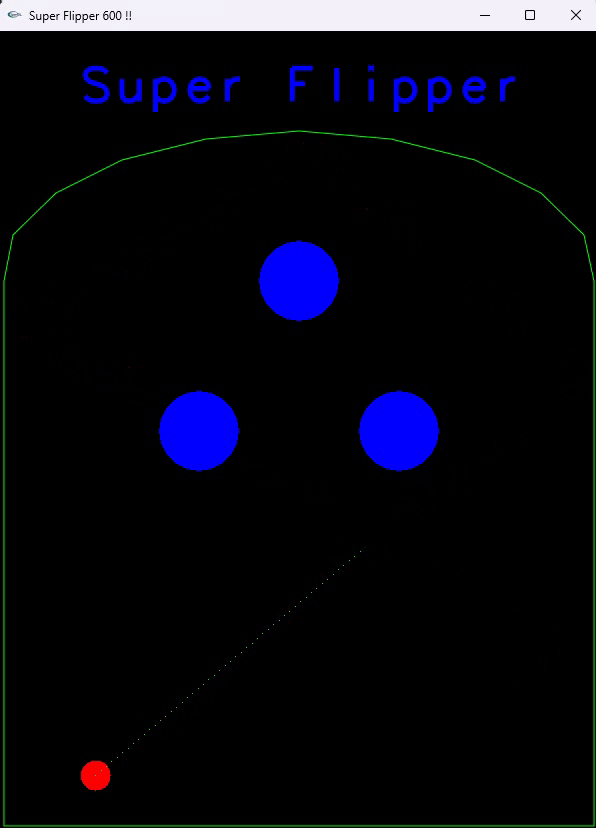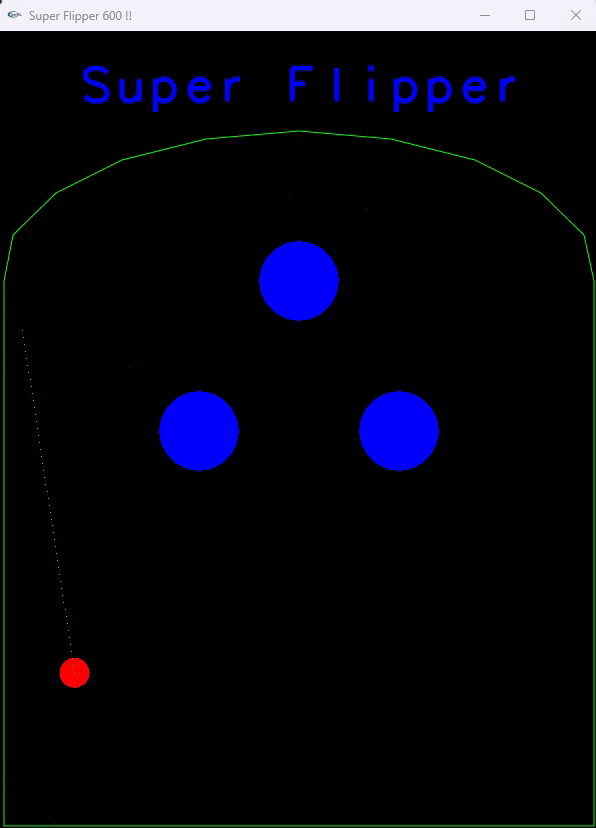
../_images/rebondsV2.gif

Avertissement

Il existe des cas pathologiques. En effet, la bille peut venir taper pile à la jonction de deux segments. Si vous programmez votre gestionnaire de collision de manière à déclencher un rebond pour chaque collision détectée, alors deux rebonds seront effectués et finalement le vecteur déplacement de la bille va rester inchangé et elle traversera alors la bordure, à votre grand désarroi. Pour éviter cette situation, on va faire en sorte qu’un seul rebond se produise en utilisant l’algorithme de principe suivant :

NewDir = Bille.CurrentDir  // cas : pas de rebond

if (collision1)  NewDir = Rebond(Bille.CurrentDir...)
if (collision2)  NewDir = Rebond(Bille.CurrentDir...)
if (collision3)  NewDir = Rebond(Bille.CurrentDir...)

Bille.CurrentDir = NewDir

Cibles

Certaines pièces disparaissent une fois touchées en rapportant des points. Ce sont les cibles.

../_images/target.png

Modélisation

Une cible est modélisée dans le jeu par un segment. Veillez à respecter les règles de placement suivantes :

  • Les cibles sont orientées dans une direction oblique (non verticale / non horizontale).

  • Toutes les cibles ont la même longueur, longueur supérieure au diamètre de la bille.

  • On trouve deux rangées de plusieurs cibles, une sur le coté gauche et l’autre sur le coté droit, symétriques par rapport à l’axe vertical du flipper.

  • Dans chaque rangée, les cibles sont alignées et légèrement espacées.

  • Une rangée contient de 3 à 5 cibles.

Détection de la collision

Nous avons traité le cas de l’intersection entre la bille et un segment précédemment. Nous allons cependant traiter cette fois les trois zones de collision, la bille pouvant provenir de n’importe où autours des cibles.

Logique de fonctionnement

Une fois touchée, une cible s’enfouit sous le décors et n’est plus active. Voici les règles de comportement de ces objets :

  • Au début du jeu, chaque cible est verte et active. Pour la représenter, on dessine un segment vert et épais de quelques pixels. Pour dessiner un segment épais, il suffit de tracer plusieurs segments décalés d’un pixel vers la droite par exemple.

  • Une fois touchée, une cible devient rouge et ne collisionne plus avec la bille. On dessine un seul segment pour la réprésenter.

  • Lorsque toutes les cibles d’une même rangée sont touchées, elles sont toutes réactivées.

Plusieurs informations doivent être stockées :

  • Position/direction d’une cible

  • État d’une cible

  • Appartenance d’une cible à une certaine rangée

Plusieurs choix de modélisation sont possibles :

  • Une structure Rangée et une structure Cible, la structure Rangée contenant la liste des cibles qu’elle gère.

  • Une structure Cible et deux listes de cibles chacune représentant une rangée.

  • Une structure Cible et une liste de cibles. Chaque cible doit inclure l’identifiant de la rangée à laquelle elle appartient.

Prenez le choix que vous pensez le mieux maîtriser.

Les bumpers

Les bumpers correspondent à des mécanismes de forme circulaire faisant rebondir la bille énergiquement :

../_images/bumper.png

Détection de collision Cercle/Cercle

La bille et les bumpers peuvent se modéliser dans le jeu par des cercles. Ainsi, pour détecter la collision entre la bille et un bumper, il faut détecter l’intersection entre deux cercles. Ce cas est relativement facile à gérer.

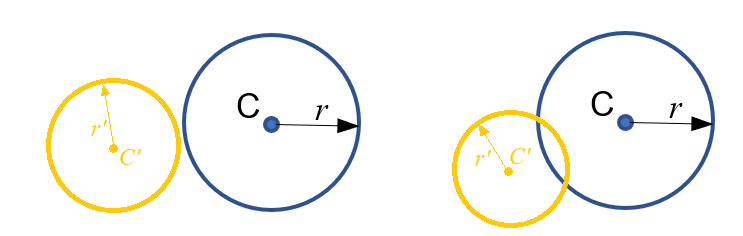
../_images/interCircleCircle.png

En effet, il suffit de vérifier que la distance entre les deux centres est inférieure à la somme des deux rayons r+r' et dans ce cas, il y a collision.

Gestion du rebond

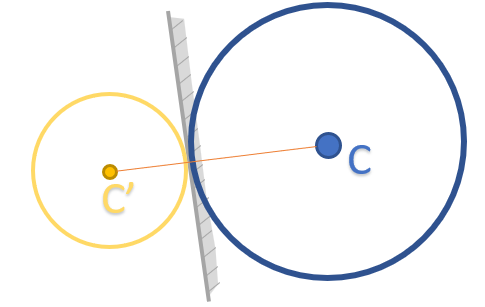
Nous allons gérer le rebond de la bille sur un bumper de manière similaire au rebond de la bille contre un bord. En effet, lorsque les deux cercles rentrent en contact, ils sont tangents en un point. Le rebond se gère comme si la bille heurtait un mur passant par ce point de contact et de direction perpendiculaire au segment reliant les deux centres des cercles.

Le vecteur normal utilisé par la fonction Rebond() correspond au vecteur \(\overrightarrow{CC'}\) normalisé :

../_images/collisionCercle.png

Dessiner un flash

Lorsqu’il y a une collision, dessinez un flash sous le bumper qui disparaît progressivement en 1 seconde :

../_images/bumpflash.png

Pour cela, il faut utiliser une structure Bumper contenant les informations suivantes :

  • La position du Bumper.

  • Son rayon.

  • Un horodatage T0 (timestamp) indiquant l’instant où a eu lieu la dernière collision avec la bille.

Quelques petits conseils :

  • La valeur \(dt=t-T0\) indique le temps écoulé depuis la dernière collision.

  • Le flash s’affiche lorsque \(0 \le t \le 1\).

  • Pour l’animation du flash, le rayon doit passer de RBig à RBumper en 1 seconde. On peut utiliser la formule : \(R(t) = RBig - (RBig-RBumper)*dt\).

  • La fonction G2D::elapsedTimeFromStartSeconds() retourne un flottant indiquant le temps écoulé en secondes depuis le début du jeu.

Finalisation

Placez trois bumpers dans le flipper. Chaque bumper doit être suffisamment éloigné des autres objets pour permettre à la bille de circuler.

Score

Les collisions rapportent des points et augmentent le score :

  • Bumper : 100 points

  • Cibles : 500 points

  • Rangée complète : bonus de 1111 points

Affichez le score en haut de la fenêtre de jeu. Vous pouvez retirer le titre si la place manque.